舞蹈链——你也想起舞吗?
Dancing Links X 求解精确覆盖
舞蹈链能够解决这样的一类问题:
给你一个 \(01\) 矩阵,要求你选择一些行,使得所以列上都有其只有一个 \(1\) 在这里面出现。
因为数独问题能够转化成上面这个问题,所以 DLX 是解决数独问题的有力工具。
1 简介
无没有在百度百科上找到
2 算法讲解
这样的一个题,暴力怎么做?我们肯定是随便选一个节点,然后选这个节点所代表的的这一行,与此同时,代价是所以与这一行有交的行都不能选了。这是一个删除的过程,因为要回溯,我们同时也需要考虑如果恢复。
有一个高效的数据结构可以快速维护这个过程——舞蹈链。
舞蹈链是一个十字循环双向链表,众所周知链表可以方便的插入和删除,所以舞蹈链也擅长这个。我们来看舞蹈链是如何解决上面这个问题的。
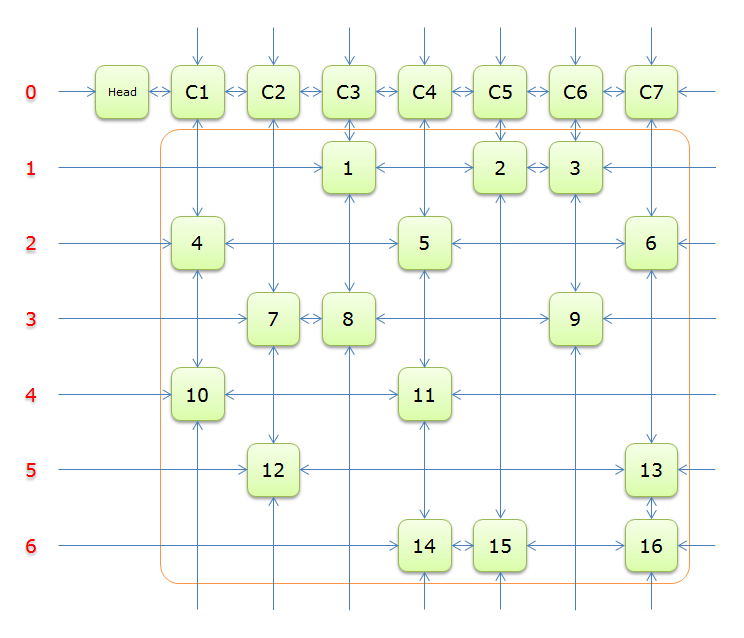
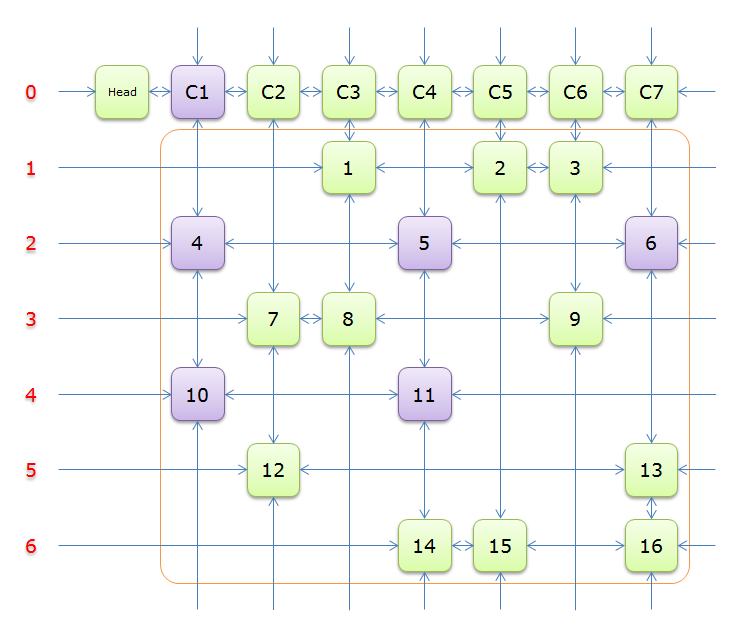
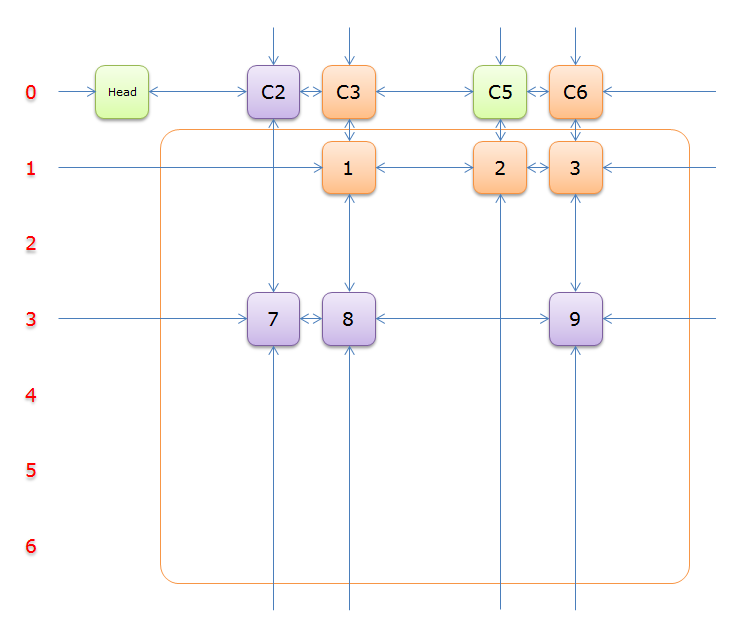
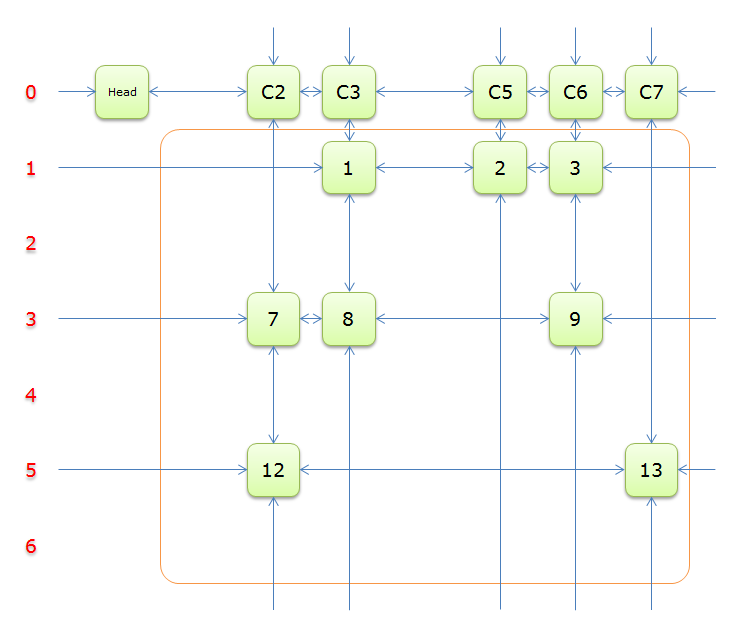
这是一个舞蹈链,其中第一行是虚拟节点,其余节点与 \(01\) 矩阵上的 \(1\) 一一对应。
2.1 初始化
inline void init(int n){
this->n=n;
for(int i=0;i<=n;i++) u[i]=i,d[i]=i,l[i]=i-1,r[i]=i+1;
l[0]=n;r[n]=0;
size=n+1;
memset(s,0,sizeof(s));
}
比较简单不作讲解。
2.2 建舞蹈链
inline void addrow(int vr,vector<int> vc){
int first=size;
for(int i=0;i<vc.size();i++){
int c=vc[i];
l[size]=size-1;r[size]=size+1;u[size]=u[c];d[size]=c;
d[u[c]]=size;u[c]=size;
row[size]=vr;col[size]=c;
s[c]++;size++;
}
r[size-1]=first;l[first]=size-1;
}
注意这里 \(vr\) 是行号,然后 \(vc\) 里边存的是这一行是 \(1\) 的节点的列号是多少。
加入一行的时候注意维护循环链表。
2.3 删除与恢复
#define For(i,a,x) for(int i=a[x];i!=x;i=a[i])
inline void remove(int c){
l[r[c]]=l[c];
r[l[c]]=r[c];
For(i,d,c) For(j,r,i){
u[d[j]]=u[j];d[u[j]]=d[j];--s[col[j]];
}
}
inline void restore(int c){
For(i,u,c) For(j,l,i){
++s[col[j]];d[u[j]]=j;u[d[j]]=j;
}
r[l[c]]=c;
l[r[c]]=c;
}
注意我们的参数 \(c\) 是列号,也可以指这一列的那个虚拟节点(虚拟节点的编号是 \(0\) 到 \(n\) ,其中 \(n\) 是列数)
我们删除了这一列(把虚拟节点断开),同时删除了每一个 \(1\) 节点所在行与其他行的联系。我们只是断开了联系,但内部并没有切断。
2.4 递归寻找解
inline bool dfs(int deep){
if(r[0]==0){
anstail=deep;
return 1;
}
int c=r[0];
For(i,r,0) if(s[i]<s[c]) c=i;
remove(c);
For(i,d,c){
ans[deep]=row[i];
For(j,r,i) remove(col[j]);
if(dfs(deep+1)) return 1;
For(j,l,i) restore(col[j]);
}
restore(c);
return 0;
}
其中 \(deep\) 指的是选到第几行了,由循环链表可以知道,当虚拟节点右边连到自己时,整张图就都被删完了,而这就对应我们找到了一组解。我们找到列节点数最小的一个节点,因为这样产生的影响最小。注意,因为回溯,删除和恢复的顺序要反过来,否则会 WA 的很惨。对应的,我们选完一列后,我们删除这一列,并删除这一列所有 \(1\) 节点所在行的所有 \(1\) 节点所在列,显然,这些被删除的行都不能选了。
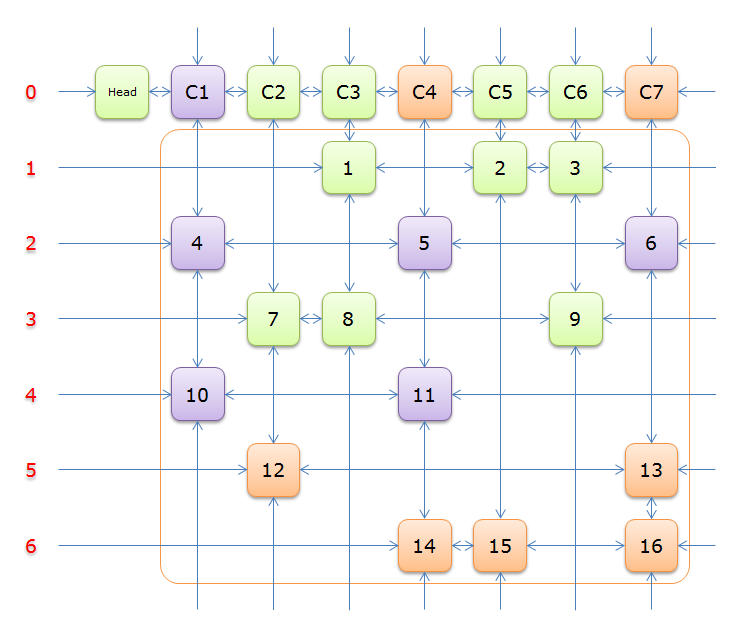
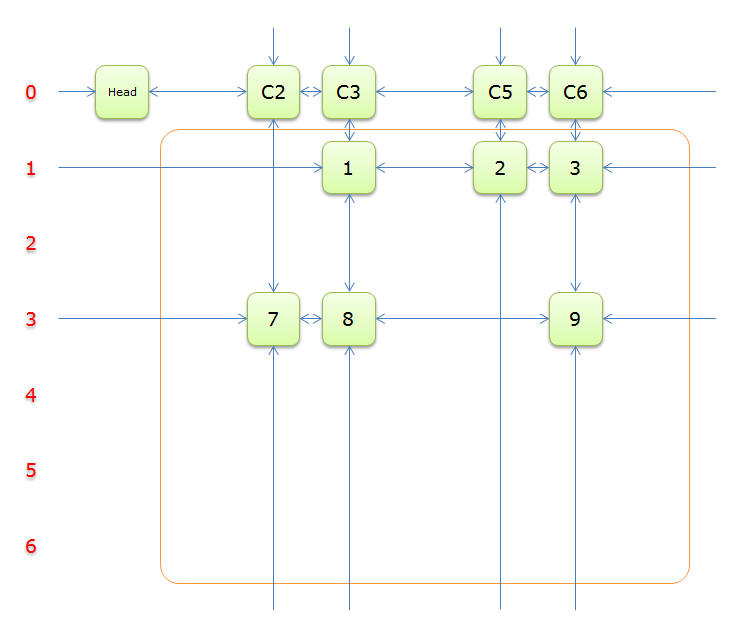
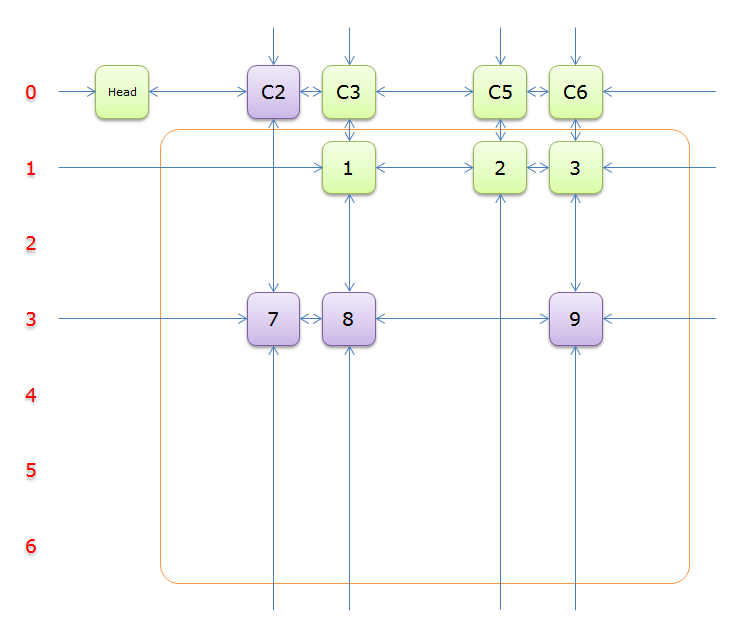
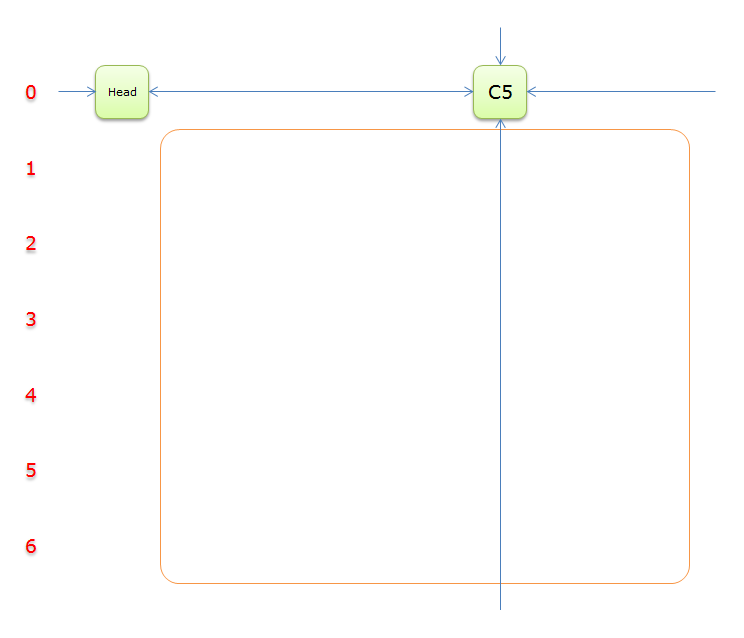
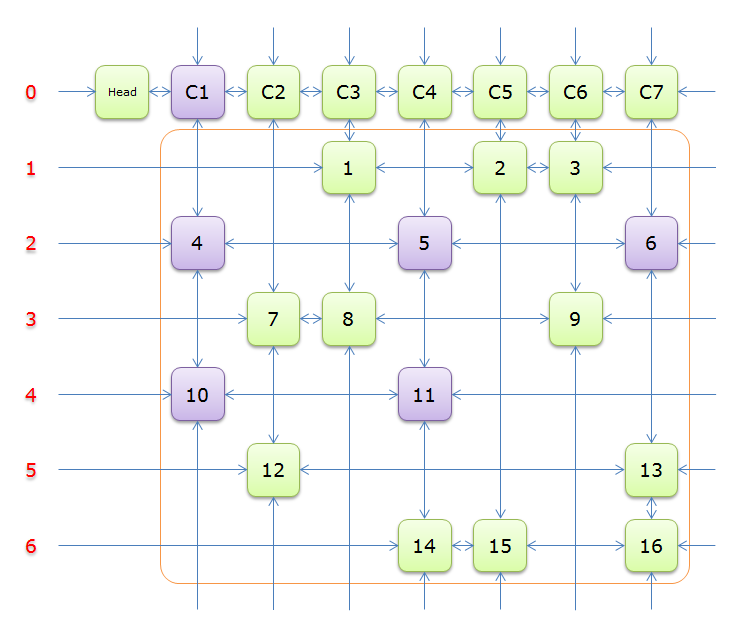
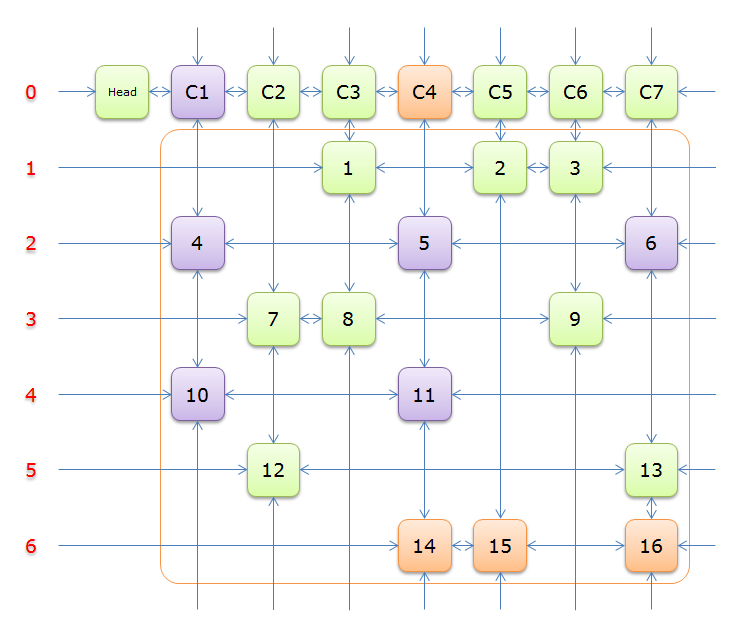
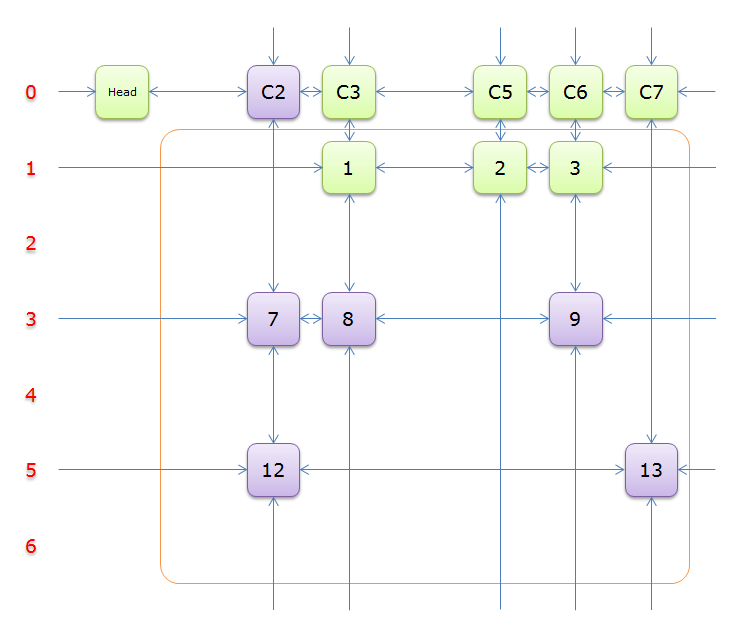
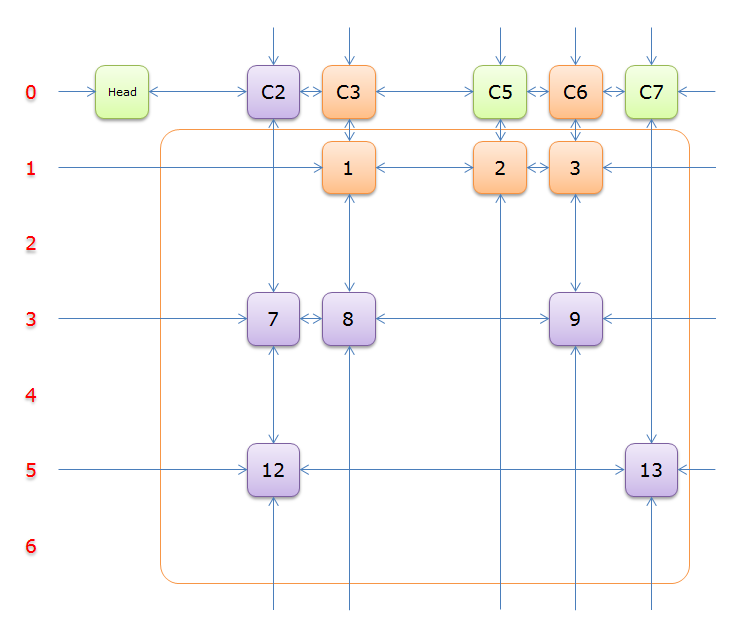
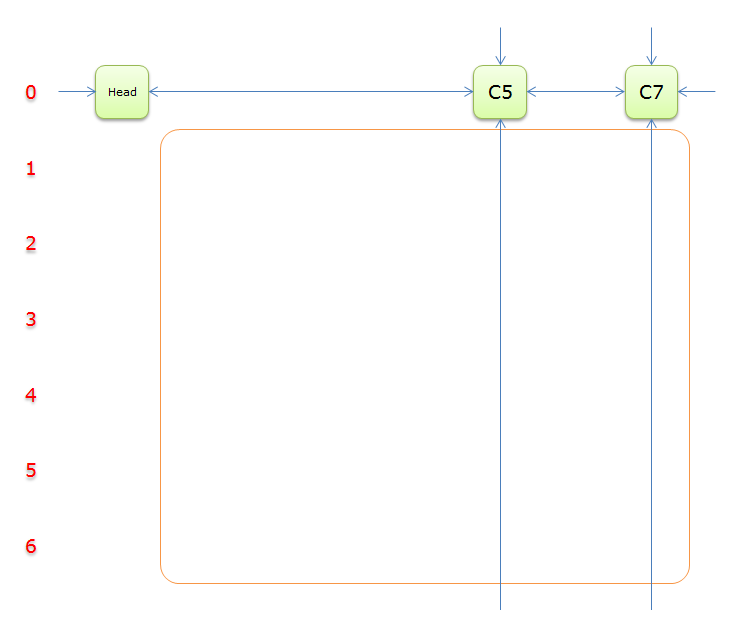
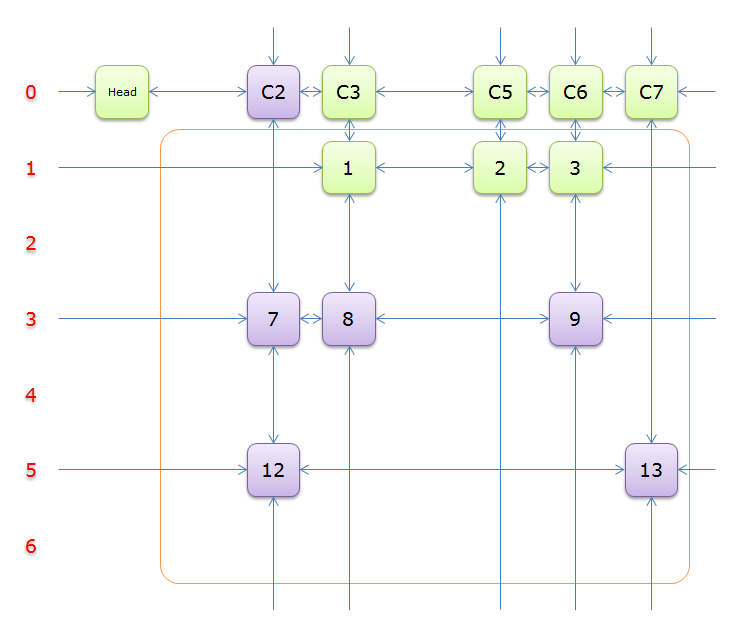
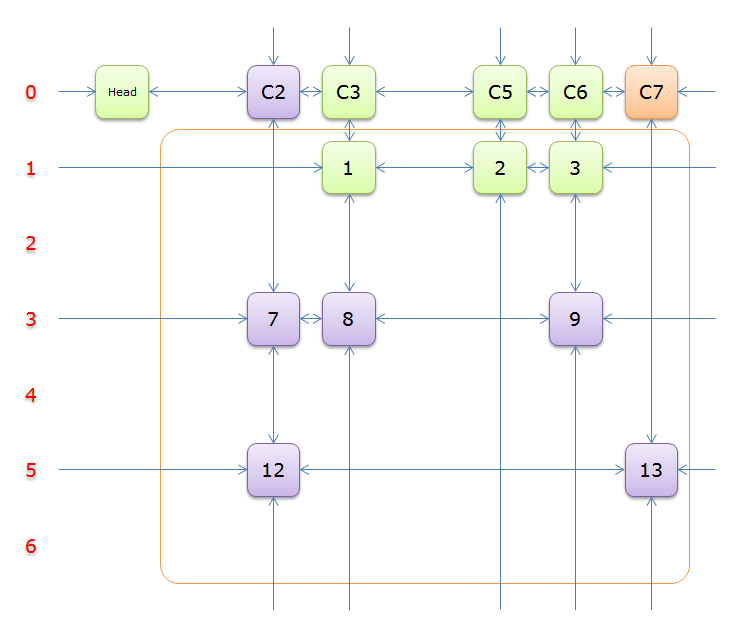
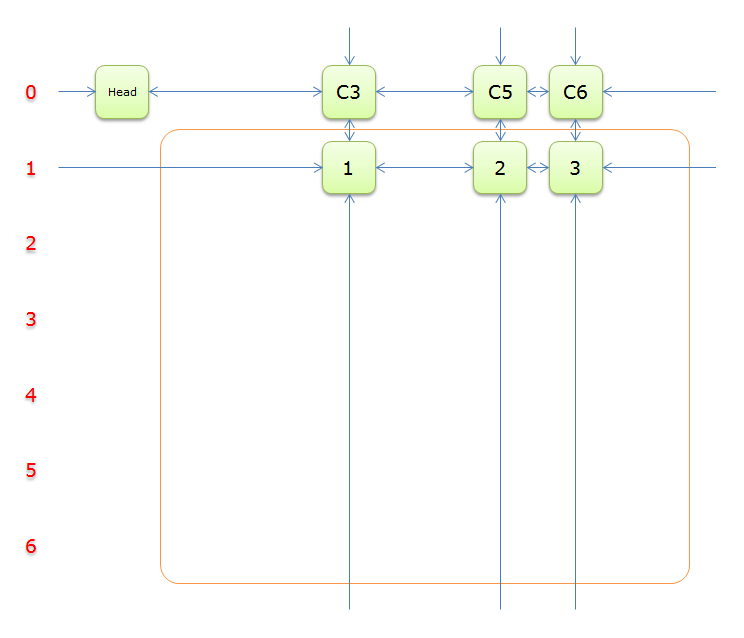
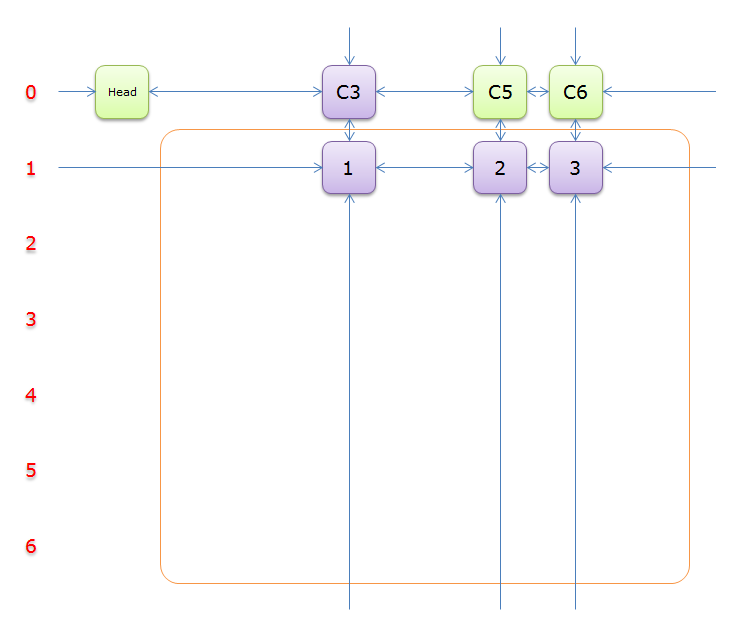
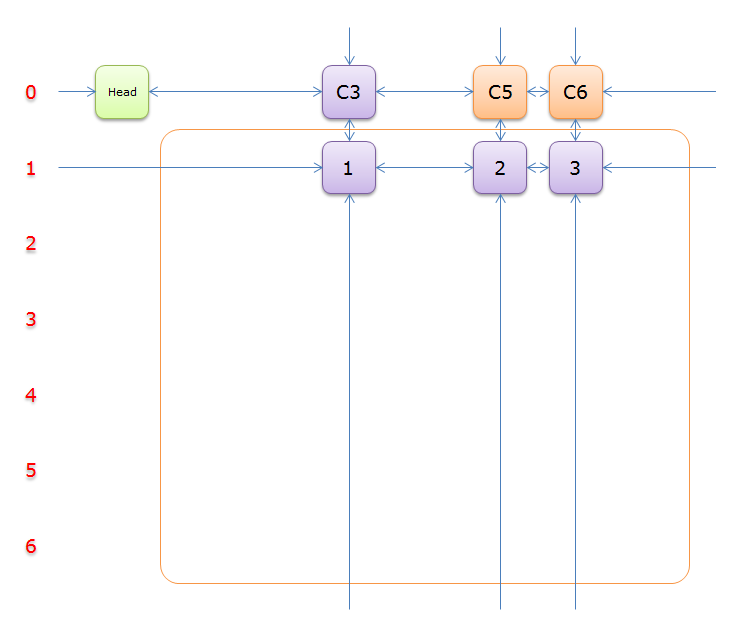
2.5 图解
下列图解引用自最下方的引用博客。其中,紫节点是我们 \(2.4\) 中第 \(8\) 行要删除的节点,而紫色节点是第 \(11\) 行。恢复是对应的。