平衡树入门——Splay
平衡树入门——Splay
一种自带大常数的平衡树,但是 LCT 要用到它,所以今天学了一下。
1 简介
伸展树(Splay Tree),也叫分裂树,是一种二叉排序树,它能在 \(O(\log n)\) 内完成插入、查找和删除操作。它由丹尼尔·斯立特 Daniel Sleator 和 罗伯特·恩卓·塔扬 Robert Endre Tarjan 在1985年发明的。
在伸展树上的一般操作都基于伸展操作:假设想要对一个二叉查找树执行一系列的查找操作,为了使整个查找时间更小,被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法, 在每次查找之后对树进行重构,把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。伸展树是一种自调整形式的二叉查找树,它会沿着从某个节点到树根之间的路径,通过一系列的旋转把这个节点搬移到树根去。
它的优势在于不需要记录用于平衡树的冗余信息。
2 数据结构剖析
Splay 的左旋和右旋操作和 Treap 是一样的,不过因为 Splay 并没有记录其余信息,所以它旋转的“理由”和 Treap 不一样,但其实都是为了均摊复杂度。多次旋转只是一个使用概率的问题。
2.1 其他函数与结构体
结构体一共打包了这些东西:
struct point{
int size,cnt,val,ch[2],fa;
};
point p[N];
其中 \(size\) 指的是子树大小,\(cnt\) 是这个权值的出现次数,\(val\) 是这个节点代表的权值,\(ch_0,ch_1\) 分别是左右节点,\(fa\) 值得是父亲节点。
这些其他函数包括:
pushup合并信息的一个函数
inline void pushup(int k){
p[k].size=p[p[k].ch[0]].size+p[p[k].ch[1]].size+p[k].cnt;
}
clear清理节点
inline void clear(int k){
p[k].size=p[k].ch[0]=p[k].cnt=p[k].ch[1]=p[k].val=p[k].fa=0;
}
get判断这个节点是其父亲的左儿子还是右儿子
inline int get(int k){
return k==p[p[k].fa].ch[1];
}
new_node添加一个新节点
inline void new_node(int val){
++tot;p[tot].val=val;p[tot].size=1;p[tot].cnt=1;
}
2.2 旋转
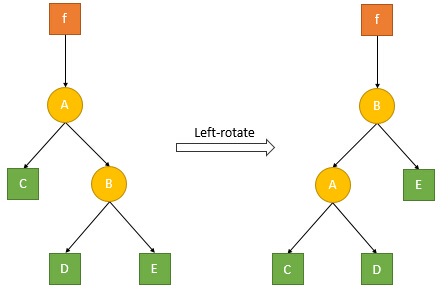
还是和 Treap 一样的左旋和右旋,不过 Splay 的左旋右旋需要分两种情况讨论:
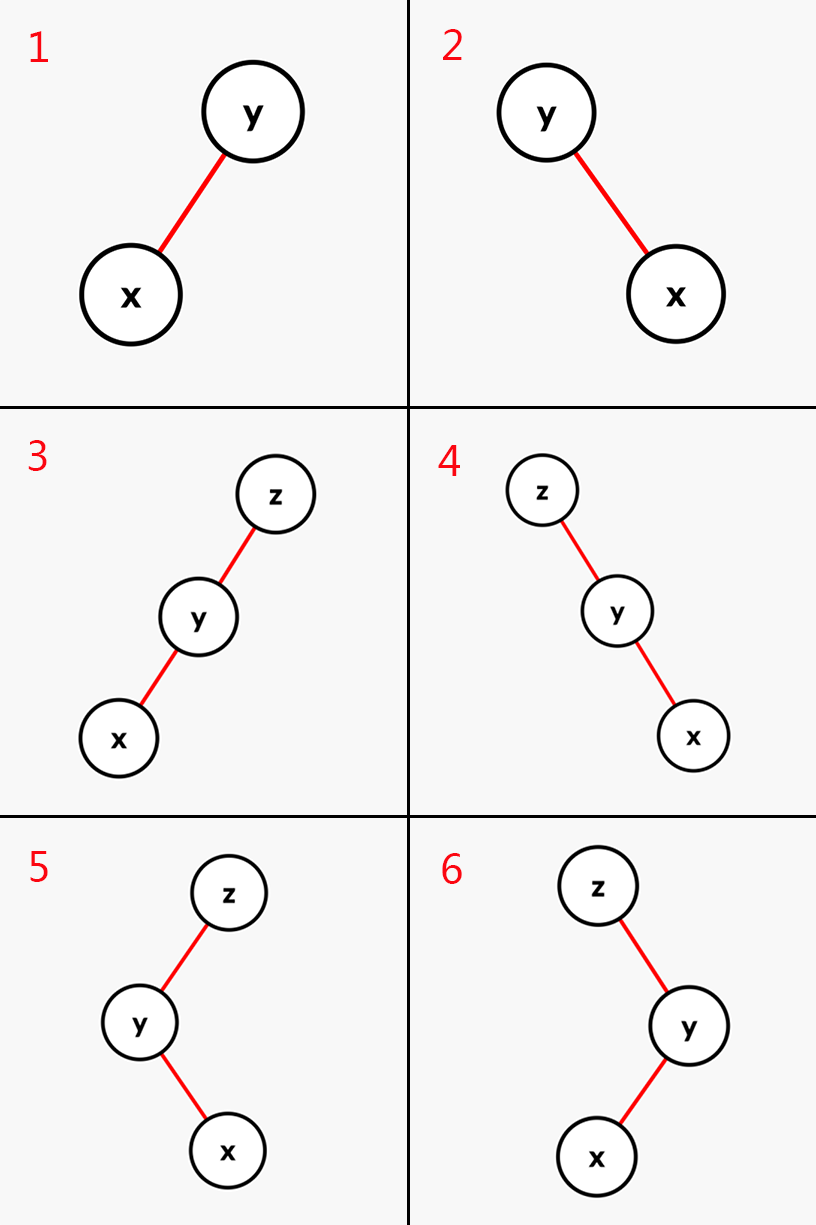
-
当父亲是根节点的时候(图 \(1,2\)),直接旋转就可以了。
-
当父亲和爷爷在一条直线上的时候,要先旋转父亲再旋转儿子。(图 \(2,3\) )
-
如果不在一条直线上,那么我们就先左旋或右旋儿子,或者先右旋再左旋儿子。
至于情况 \(2\) 为什么要先旋转父亲,在旋转儿子,这里挂上势能分析法的博客,可以证明,如果不这样旋转,实际上树的深度是不能减小的,可以卡成 \(O(n^2)\) ,而这样旋转的复杂度均摊下来是 \(O(n\log n)\) 的。
在下面的代码中,左旋和右旋写到了一个函数里。
inline void rotate(int k){
int y=p[k].fa,z=p[y].fa,which=get(k),which2=get(y);
p[y].ch[which]=p[k].ch[which^1];
if(p[y].ch[which]) p[p[y].ch[which]].fa=y;
p[k].ch[which^1]=y;
if(z) p[z].ch[which2]=k;
p[y].fa=k;p[k].fa=z;
pushup(y);pushup(k);
}
2.3 Splay 操作
这个操作指的是把某一个节点按照上面的旋转规则旋转到根节点。在伸展树中的所有除了删除的其他操作都需要 Splay 一下,原因是一个使用概率的问题,被访问过的元素使用概率会比较高。Splay 操作之后不要忘记更新根节点!
inline void splay(int k){
for(int fa=p[k].fa;fa=p[k].fa,fa;rotate(k)){
if(p[fa].fa) rotate(get(fa)==get(k)?fa:k);
}
root=k;
}
2.4 查询排名&查询权值
基本思想和 Treap 大致相同,只是最后需要 Splay 一下,代码也写成非递归版了。
inline int getrank(int val){
int rank=0,k=root;
while(k)
if(val<p[k].val) k=p[k].ch[0];
else{
rank+=p[p[k].ch[0]].size;
if(val==p[k].val){
splay(k);return rank+1;
}
rank+=p[k].cnt;k=p[k].ch[1];
}
return INF;
}
inline int getval(int rank){
int k=root;
while(k)
if(rank<=p[p[k].ch[0]].size) k=p[k].ch[0];
else{
rank-=p[p[k].ch[0]].size+p[k].cnt;
if(rank<=0){
splay(k);return p[k].val;
}
k=p[k].ch[1];
}
return INF;
}
2.5 查询前驱后继
考虑到因为可能这个节点在树种就不存在,所以我们先插入这个节点,然后找前驱后继就非常方便——因为 Splay 操作,这个节点已经是根节点,前驱就是左子树中最右边的节点,后继就是右子树中最左边的节点,直接找就可以。最后我们把这个节点删除,删除操作一会再说。插入与删除操作体现在主函数中,这里只挂上插入后查询的代码。最后不要忘记 Splay 操作。
inline int getpre(){
int k=p[root].ch[0];
if(!k) return INF;
while(p[k].ch[1]) k=p[k].ch[1];
splay(k);return k;
}
inline int getnext(){
int k=p[root].ch[1];
if(!k) return INF;
while(p[k].ch[0]) k=p[k].ch[0];
splay(k);return k;
}
2.6 删除操作
基本思路是要把删除的那个节点 Splay 到根节点上来,然后合并一下左右子树。
详细来说,首先把节点旋转上来,然后看这个节点的 \(cnt\) ,如果不为 \(1\) ,那么直接减就可以,否则我们讨论如下:
-
左右子树都为空。
我们直接销毁掉这个节点。
-
左右子树有一个为空。
把那个不空的子树旋转上来,销毁跟节点。
-
左右子树都不为空。
我们考虑合并两颗子树,显然我们需要找到左子树中最大的那个节点来充当新树的跟。这个节点就是现在根节点的前驱,所以我们直接查询这个根节点的前驱,这样前驱就被 Splay 到了根上。我们可以发现,当这个前驱被旋转到左子树的根节点上时,由于它是左子树最大的,所以它没有右儿子,通过画图不难得出,再前驱与根节点交换后,根节点变成了前驱的右儿子且根节点没有左儿子,所以我们就可以像删除链表上的元素一样删除这个节点了。
inline void delete_(int k){
getrank(k);
if(p[root].cnt>1){
p[root].cnt--;pushup(root);return;
}
if(!p[root].ch[0]&&!p[root].ch[1]){
clear(root);root=0;return;
}
if(p[root].ch[0]==0||p[root].ch[1]==0){
int which=p[root].ch[0]==0?0:1,now=root;
root=p[root].ch[which^1];p[root].fa=0;clear(now);return;
}
int now=root,pre=getpre();
p[p[now].ch[1]].fa=pre;
p[pre].ch[1]=p[now].ch[1];
clear(now);pushup(root);
}
3 总代码
#include<bits/stdc++.h>
#define dd double
#define ld long double
#define ll long long
#define uint unsigned int
#define ull unsigned long long
#define N 3000000
#define M number
using namespace std;
const int INF=0x3f3f3f3f;
template<typename T> inline void read(T &x) {
x=0; int f=1;
char c=getchar();
for(;!isdigit(c);c=getchar()) if(c == '-') f=-f;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
x*=f;
}
struct point{
int size,cnt,val,ch[2],fa;
};
point p[N];
struct Splay{
int root,tot;
inline void pushup(int k){
p[k].size=p[p[k].ch[0]].size+p[p[k].ch[1]].size+p[k].cnt;
}
inline void clear(int k){
p[k].size=p[k].ch[0]=p[k].cnt=p[k].ch[1]=p[k].val=p[k].fa=0;
}
inline int get(int k){
return k==p[p[k].fa].ch[1];
}
inline void rotate(int k){
int y=p[k].fa,z=p[y].fa,which=get(k),which2=get(y);
p[y].ch[which]=p[k].ch[which^1];
if(p[y].ch[which]) p[p[y].ch[which]].fa=y;
p[k].ch[which^1]=y;
if(z) p[z].ch[which2]=k;
p[y].fa=k;p[k].fa=z;
pushup(y);pushup(k);
}
inline void splay(int k){
for(int fa=p[k].fa;fa=p[k].fa,fa;rotate(k)){
if(p[fa].fa) rotate(get(fa)==get(k)?fa:k);
}
root=k;
}
inline void new_node(int val){
++tot;p[tot].val=val;p[tot].size=1;p[tot].cnt=1;
}
inline void insert(int val){
if(!root){
new_node(val);root=tot;
return;
}
int k=root,fa=0;
while(1){
if(p[k].val==val){
p[k].cnt++;pushup(k);pushup(fa);
splay(k);break;
}
fa=k;k=p[k].ch[p[k].val<val];
if(!k){
new_node(val);p[fa].ch[p[fa].val<val]=tot;
p[tot].fa=fa;pushup(tot);pushup(fa);splay(tot);break;
}
}
}
inline int getrank(int val){
int rank=0,k=root;
while(k)
if(val<p[k].val) k=p[k].ch[0];
else{
rank+=p[p[k].ch[0]].size;
if(val==p[k].val){
splay(k);return rank+1;
}
rank+=p[k].cnt;k=p[k].ch[1];
}
return INF;
}
inline int getval(int rank){
int k=root;
while(k)
if(rank<=p[p[k].ch[0]].size) k=p[k].ch[0];
else{
rank-=p[p[k].ch[0]].size+p[k].cnt;
if(rank<=0){
splay(k);return p[k].val;
}
k=p[k].ch[1];
}
return INF;
}
inline int getpre(){
int k=p[root].ch[0];
if(!k) return INF;
while(p[k].ch[1]) k=p[k].ch[1];
splay(k);return k;
}
inline int getnext(){
int k=p[root].ch[1];
if(!k) return INF;
while(p[k].ch[0]) k=p[k].ch[0];
splay(k);return k;
}
inline void delete_(int k){
getrank(k);
if(p[root].cnt>1){
p[root].cnt--;pushup(root);return;
}
if(!p[root].ch[0]&&!p[root].ch[1]){
clear(root);root=0;return;
}
if(p[root].ch[0]==0||p[root].ch[1]==0){
int which=p[root].ch[0]==0?0:1,now=root;
root=p[root].ch[which^1];p[root].fa=0;clear(now);return;
}
int now=root,pre=getpre();
p[p[now].ch[1]].fa=pre;
p[pre].ch[1]=p[now].ch[1];
clear(now);pushup(root);
}
};
Splay sp;
int n;
int main(){
read(n);
for(int i=1;i<=n;i++){
int op,x;read(op);read(x);
if(op==1) sp.insert(x);
else if(op==2) sp.delete_(x);
else if(op==3) printf("%d\n",sp.getrank(x));
else if(op==4) printf("%d\n",sp.getval(x));
else if(op==5) sp.insert(x),printf("%d\n",p[sp.getpre()].val),sp.delete_(x);
else if(op==6) sp.insert(x),printf("%d\n",p[sp.getnext()].val),sp.delete_(x);
}
}


