平衡树入门——Treap
平衡树入门——Treap
挖坑一直爽,一直挖坑一直爽。这个坑大概鸽了一年。
1 平衡树
平衡树(Balance Tree,BT) 指的是,任意节点的子树的高度差都小于等于1。常见的符合平衡树的有,B树(多路平衡搜索树)、AVL树(二叉平衡搜索树)等。平衡树可以完成集合的一系列操作, 时间复杂度和空间复杂度相对于“2-3树”要低,在完成集合的一系列操作中始终保持平衡,为大型数据库的组织、索引提供了一条新的途径。
\(Treap\) 是每个 OIer 入门必学平衡树。
2 变量简介
2.1 节点
struct node{
int size,cnt;
int val,rad;
int l,r;
};
node tree[N];
int tail,root;
其中 \(size\) 是这颗子树的大小,\(cnt\) 表示的是这个节点所代表权值的个数,\(val\) 表示的是节点代表权值,\(rad\) 是一个随机数,随机是因为 Treap 为了保持其平衡,同时维护堆的性质,这样复杂度就有了保障。
2.2 合并信息
inline void pushup(int k){
tree[k].size=tree[tree[k].l].size+tree[tree[k].r].size+tree[k].cnt;
}
比较显然,不做讲解。
2.3 左右旋
inline void zip(int &k){
int kr=tree[k].r;
tree[k].r=tree[kr].l;tree[kr].l=k;
pushup(k);pushup(kr);k=kr;
}
inline void zap(int &k){
int kl=tree[k].l;
tree[k].l=tree[kl].r;tree[kl].r=k;
pushup(k);pushup(kl);k=kl;
}
第一个函数是左旋,第二个是右旋。为了维护这是为了维护堆的性质,同时必须满足 BST 的性质。
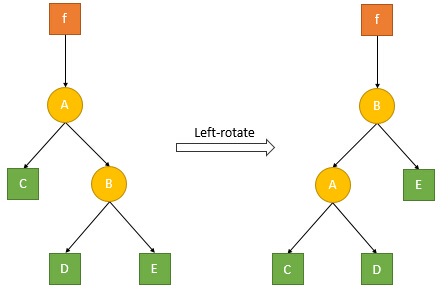
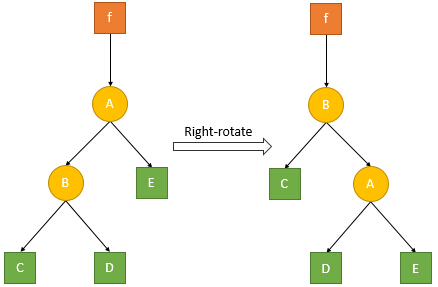
通过图片不难理解上面的代码。
2.4 建立新节点
inline int New(int val){
tree[++tail].val=val;
tree[tail].size=tree[tail].cnt=1;
tree[tail].rad=rand();
return tail;
}
2.5 插入与删除
inline void insert_(int &k,int val){
if(tail==0) k=0;
if(!k) k=New(val);
else if(val==tree[k].val) tree[k].cnt++;
else if(val<tree[k].val){
insert_(tree[k].l,val);
if(tree[tree[k].l].rad>tree[k].rad) zap(k);
}
else{
insert_(tree[k].r,val);
if(tree[tree[k].r].rad>tree[k].rad) zip(k);
}
pushup(k);
}
插入实际上就是在为这个权值找一个新的位置,与此同时维护一下堆的性质,最后合并就可以了。
inline void delete_(int &k,int val){
if(!k) return;
if(val==tree[k].val){
if(tree[k].cnt>1){
tree[k].cnt--;
}
else if(!tree[k].l&&!tree[k].r) k=0;
else{
if(!tree[k].r||tree[tree[k].l].rad>tree[tree[k].r].rad){
zap(k);
delete_(tree[k].r,val);
}
else{
zip(k);
delete_(tree[k].l,val);
}
}
}
else val<tree[k].val?delete_(tree[k].l,val):delete_(tree[k].r,val);
pushup(k);
}
我们希望把删除节点旋转到叶子节点上进行删除,当然进行这个操作得必须是这个点的 \(cnt\) 在删除之前为 \(1\)
。注意在旋转的过程中,还是要小心维护其堆得性质,同时因为我们的引用符号,我们直接在旋转到叶子节点之后让 \(k=0\) 就完成了删除,非常方便。
2.6 查询前驱后继,按排名找值,按值找排名
inline int getrank(int k,int val){
if(!k) return -INF;
if(tree[k].val==val) return tree[tree[k].l].size+1;
if(val<tree[k].val) return getrank(tree[k].l,val);
return getrank(tree[k].r,val)+tree[tree[k].l].size+tree[k].cnt;
}
inline int getval(int k,int rank){
if(!k) return -INF;
if(tree[tree[k].l].size>=rank) return getval(tree[k].l,rank);
if(tree[tree[k].l].size+tree[k].cnt>=rank) return tree[k].val;
return getval(tree[k].r,rank-tree[tree[k].l].size-tree[k].cnt);
}
inline int getpre(int k,int val){
if(!k) return -INF;
if(tree[k].val>=val) return getpre(tree[k].l,val);
else return Max(tree[k].val,getpre(tree[k].r,val));
}
inline int getnext(int k,int val){
if(!k) return INF;
if(tree[k].val<=val) return getnext(tree[k].r,val);
else return Min(tree[k].val,getnext(tree[k].l,val));
}
这个好理解,不做讲解。


