后缀树
0.一些说明
- 如果从根节点到\(k\)的路径上的字符连成的字符串是\(s\),那么称字符串\(s\)对应的节点是\(k\),节点\(k\)对应的字符串为\(s\)。
- 关于字符串的一些通用定义
- \(s_{i,j}\):字符串\(s\)的一个子串,这个子串在s中的起始下标为\(i\),终止下标为\(j\)。
- 父边:链接u的父节点和u的这条边。
1.后缀树
后缀树是一种强大的数据结构,听说用后缀数组和后缀自动机能做的题都可以用后缀树做,实际上,前三者使用起来各有千秋。
后缀树是满足这样的条件的一棵树:(一下均假定有一个长度为\(n\)的字符串\(s\))
- 它有\(n\)个叶节点
- 每个内部节点(即非叶节点)至少有2个儿子
- 从同一个节点引出的任意两条边上标的字符串都不会以相同字符开始。
- 从根节点到任意叶节点的路径上的字符连起来均为\(s\)的后缀。
后缀树是由这样的一棵树得来的:
字符串\(banana\):
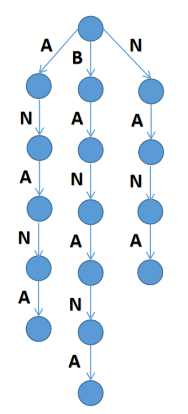
其中我们发现这棵树只有三个儿子,这是由于有一些后缀是其他后缀的前缀,解决方法就是在最后加入一个 哨兵字符,即一个在字符串\(s\)中从来没有出现过的字符,加完之后如下:
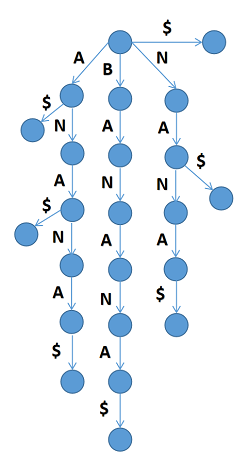
然后我们把所以度数为1点顶点删去:
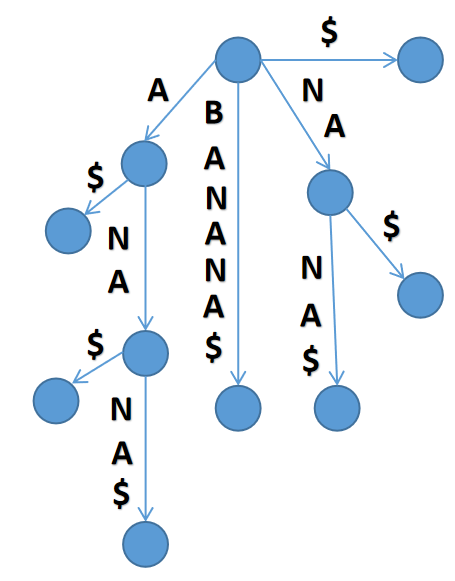
经过验证以上性质可以得到,这棵树确实是一颗后缀树。
2.构造
这里我们构造的方法为\(Ukkonen\)算法,这是一种增量构造算法,我们一次向树中插入s的每一个字符。时间复杂度:\(O(|s|)\)
2.1暴力构造
暴力怎么做?暴力是不是!加边,加边,加边,然后,并查集查询
我们一次插入每一个字符的暴力方法如下(我们先不考虑哨兵字符的事情):
假设我们插入的字符串为\(abbbc\):
插入\(a\):
插入\(b\):
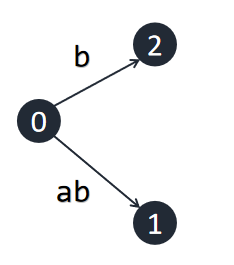
插入\(b\):
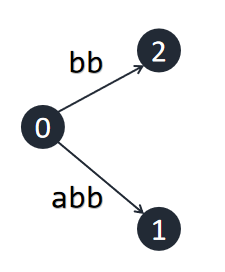
这样你会发现这个后缀树并不符合定义,这是因为没有哨兵字符所致,这里我们先不要管它。
插入\(b\):
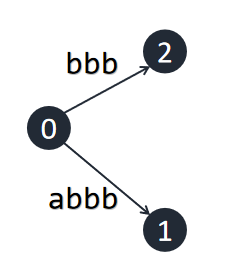
插入\(c\)(一部分):
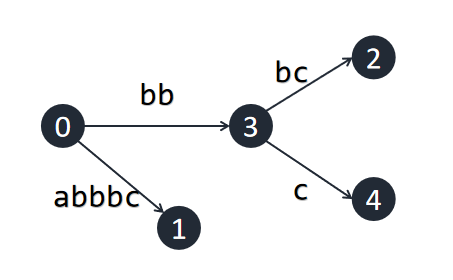
能看出,插入\(c\)后,这棵树发生了“巨变”,我们来分析一下为什么是这样的。
首先,我们插入每一个字符,实际上是要把以这个字符结尾的所有后缀插入,读者可以回顾一下之前我们插入的过程,我们从长到短插入这些后缀,插入\(abbbc\)时,没有问题,插入\(bbbc\)时,也没有问题,插入\(bbc\)时(\(BBC\)“好”啊),我们发现,我们需要在\(bbbc\)这条边上插入一个节点来插入后缀\(bbc\),由此就有了上面这张图。
下面给出插入\(c\)完毕后的图片:
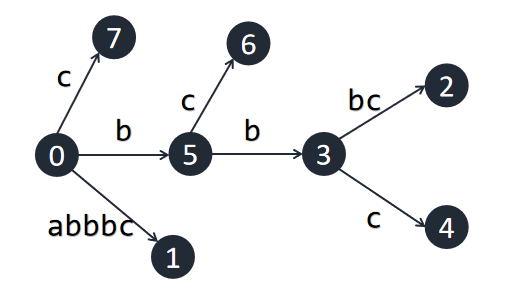
我们发现,这个算法是逼近\(O(|s|^2)\)的(枚举字符,枚举后缀并遍历后缀树),实在是太慢了,那么我们怎么优化这个算法呢?
2.2后缀链加速
给出后缀链的定义:字符串\(s\)对应的节点\(k\)的后缀链接\(su(k)\)为\(s\)的最长真后缀\(s'\)所对应的节点。
图为串 \(abbcabbd\) 的后缀树的部分后缀链接。
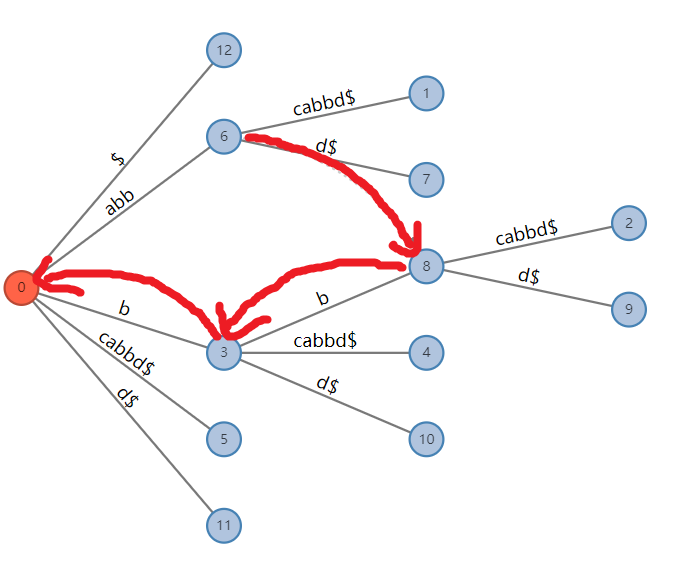
给出剩余后缀长度的定义:表示当前最长的只是隐式地包含在树中,而没有实际出现的后缀的长度,记为\(rem\),这个字符串记为\(re\)。
非常显然的是,\(re\)的所有后缀也是隐式的。
如果后缀树对应的字符串是s的话,显然有\(re=s_{n-rem+1,n}\)。
我们用\(now,len,char\),来表示\(re\),使得从节点\(now\)开始,沿着开头为字符\(char\)的边向下走\(len\)个字符,沿途经过的所有字符组成的字符串为\(re\)。
实际上,因为\(re\)是后缀,所以\(len\)一定是一段从\(now\)到某一个叶节点所经过字符的数量,容易知道不可能有两个叶节点,满足从\(now\)到这两个节点的字符数量相同(这是一颗后缀树,而没有两个相同长度的后缀),所以即使没有\(char\)我们也能还原出\(re\)来,只需要沿着\(s_{n-len+1}\)走就可以了。
下面我们先给出\(Ukkonen\)算法流程,再说明每一步的正确性。
注意:一下的根节点与上面有所不同,变成了\(1\)
2.2.1\(Ukkonen\)算法
首先创建一棵空后缀树,仅存在节点\(0\),令 \(len=0\),\(now=1\), \(n=0\) 。接下来依次对原串的每一个字符进行一轮插入。
- 首先令\(n+1\),\(len+1\)。注意到\(len\)有可能超过\(now\)的出边的长度,这时候应该沿着这条出边跳到这条出边的下一个节点,这样才能正确维护\(len\)和\(now\)。记在这一轮插入中上一个被访问的节点为\(last\),一开始令\(last=1\)。
- 找到\(now\)的开头为 \(s_{n-len+1}\)的出边。
- 如果不存在这样的出边,新建一条出边指向一个新的节点,将\(last\) 的后缀链接指向 \(now\),然后将\(last\)变为\(now\)。
- 否则,比对出边上第\(len\)个字符和将要插入的字符,
- 如果相等,则说明需要插入的后缀已经存在于后缀树之中,插入失败,同样如\(3\)中更新\(last\)的后缀链接,然后退出这轮插入。
- 如果不相等,则在第\(len\)个字符处新建一个节点\(u\) 分裂这条边,将\(last\)的后缀链接指向\(u\),并且将\(last\)变为\(u\)。然后在\(u\)处新建一条表示将要插入的字符的出边,指向另一个新建的节点。
- 如果\(now=1\),则令\(now\)跳到\(now\)的后缀链接指向的节点,否则令\(len-1\)。若 \(len=0\),结束这一轮插入。
下面先展示一下代码再做分析。
2.2.2 代码
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ld long double
#define ll long long
#define ull unsigned long long
#define N 10000
#define M number
using namespace std;
const int INF=0x3f3f3f3f;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct suffixTree {
int link[N<<1],le[N<<1],start[N<<1],s[N<<1],n,tail,now,len,ch[N<<1][27];
suffixTree ():tail(1),n(0),len(0),now(1) {le[0]=INF;}
int newnode(int st,int L){
link[++tail]=1;start[tail]=st;le[tail]=L;return tail;
}
void extend(int x){
s[++n]=x;len++;
for (int last=1;len;){
while (len>le[ch[now][s[n-len+1]]])
len-=le[now=ch[now][s[n-len+1]]];
int &v=ch[now][s[n-len+1]];int c=s[start[v]+len-1];
if (!v||x==c){
link[last]=now;last=now;
if (!v) v=newnode(n,INF);
else break;
}else{
int u=newnode(start[v],len-1);
ch[u][c]=v;ch[u][x]=newnode(n,INF);
start[v]+=len-1;le[v]-=len-1;
link[last]=v=u;last=u;
} if (now==1) len--;else now=link[now];
}
}
}su;
int main(){
char s[N];
scanf("%s",s);
for(int i=0;i<strlen(s);i++){
su.extend(s[i]-'a');
cout<<su.len<<" ";
}
}
2.2.3 一些定理
在介绍定理,先请各位读者再次关注一下程序。第\(35\)到\(37\)行的函数newnode作用是建立一个新节点,注意到,如果这个字符串已经是非隐式串了,我们把长度设置的是INF,下面的定理将会揭示这么做的原因。
-
如果一个字符串是非隐式串,那么他不可能在变成隐式串。
证明:显然。
-
在插入一个新字符时,我们只用修改隐式串即可。
证明:这就是我们为什么设置成INF的原因,既然这个字符串已经不可能变成一个非隐式串,那么我们就直接“提前把所有的字符加上”,把它的长度设置为INF。这是一个非常使用的技巧,换在dp中,这叫做提前计算费用,可以有效降低时间复杂度。
2.2.4 算法分析
-
变量声明:
\(link\)为后缀链接,\(le\)为当前节点父边的字符串长度。
\(start[k]\)指结点k的父边的第一个字符在\(s\)的下标。
\(s\)指当前的字符串,\(ch\)为\(Trie\)树。
-
第一步:
注意到\(now,len\)维护的是最长隐式串位置,再加入一个新的字符时,我们先假设这个字符会带来\(re\)长度的增加,所以让\(len\)加\(1\),这么做的正确性在哪里呢?细心地读者也许一经发现,如果手摸一下上面暴力建后缀树的例子的话,\(now,len\)并没有一直在维护\(re\),并且当且仅当这个后缀树不存在\(re\)时。为什么这么做正确形是正确的?仔细思考后可以得到,在不存在\(re\)的时候,\(now,len\)维护的这个串其实并不重要,因为我们接下来所有的操作都是针对隐式串的,如果你对上面的代码进行模拟的话会发现,在第\(44\)行的的\(if\)语句里,执行的是\(link[1]=1,1=1\),因为这时候\(now=1,last=1\),而对于\(len\)来说,第\(39\)行加\(1\),第\(53\)行减\(1\),相当于没加没减,而整个程序,除非有增加节点的必要的话,其他什么也没做。所以,在没有隐式串时不维护隐式串,对我们的程序没有影响。
不是很理解的读者可以用上面的代码进行调试。
其实上面的正确性也依赖于\(last\)的取值,这也是为什么last取值为1的原因。
而注意到程序的第\(41\),\(42\)行,这两行代码,主要是维护\(now,len\)的正确性,还记得我们上面说的对len的长度的限制吗?就体现在这里。对应着我们算法步骤\(1\)中的这一句话:
注意到\(len\)有可能超过\(now\)的出边的长度,这时候应该沿着这条出边跳到这条出边的下一个节点,这样才能正确维护\(len\)和\(now\)。
-
第二步
根据定理2,我们只需要从非隐式串开始修改。所以这一步就很好理解了:我们首先找到该隐式串的位置在哪里。
-
第三,四点一步
如果进入到44到47行的if中,就只有两种情况:一是这个串没有出现过,但已经到头了,这个时候需要新建结点,另一种情况是这个串已经出现过,我们不用管它,虽然它是一个隐式串,但对于这种隐式串我们的解决方案是添加哨兵字符。
-
第四点2步
否则,说明这个隐式串出现在边的正中间,我们直接插入这个字符,注意我们新建节点首先新建的是父节点,然后再是我们这一轮要建的节点。而不管是上面的4还是这一步,在更新后置连接时,更新的都是其父节点的后缀链接。


