Lyndon分解
1Lyndon 分解
1.1 一些说明
- 称 \(s_{i,j}\) 为字符串 \(s\) 下标 \(i\) 到 \(j\) 的字符组成的字符串。
- 记 \(s\in L\) 为 \(s\) 为 Lyndon 串。
- 记 \(L(s)\) 为串 \(s\) 的 Lyndon 分解。
1.2 一些定义
- 一个串为 Lyndon 串,当且仅当这个串的最小后缀就是这个串本身,或是这个串是它的所以循环表示中字典序最小的。
- 定义串 \(s\) 的 Lyndon 分解为一个字符串序列 \(a_1,a_2,...a_m,s.t.\forall i\in[1,m],a_i\in L,\forall i\in[1,m-1],a_i\geq a_{i+1}\)。
1.3 一些定理
- 如果 \(u\) 和 \(v\) 都是 Lyndon 串并且 \(u<v\) ,那么 \(uv\) 也是 Lyndon 串。
-
证明:
-
只需要证明 \(v>uv\) ,因为如果左式得证,根据条件可知定理得证。
这里只考虑 \(u\) 是 \(v\) 前缀的情形,其他情形都是显然的。
假设 \(v<uv\) ,那么必有 \(v_{len_u+1,len_v}<v\) ,与 \(v\) 的定义矛盾。
-
证毕。
- 串 \(s\) 的 Lyndon 分解是存在且唯一的。
-
证明:
-
存在性证明:初始令 \(m=|s|,a_i=s_i\) ,然后每次不断找到 \(a_i<a_{i+1}\) 并把这两个合并为一个串。这种构造显然是合法的。
-
唯一性证明:
假设存在两个 Lyndon 分解,它们前 \(i\) 个分解是一样的,即:
\[s=a_1a_2...a_ia_{i+1}a_{i+2}...a_{m_1}\\ s=a_1a_2...a_ia'_{i+1}a'_{i+2}...a'_{m_2} \]不妨设 \(len_{a_{i+1}}>len_{a'_{i+1}}\)
我们考察 \(a_{i+1}\) 在第二种分解中的对应情况。假设 \(a_{i+1}=a'_{i+1}a'_{i+2}...(a'_{i+k})_{1,t}\)
由性质可以得到 \(a_{i+1}<(a'_{i+k})_{1,t}\leq a'_{i+k}\leq a'_{i+1}< a_{i+1}\),矛盾。
-
证毕。
- 若字符串 \(v\) 和字符 \(c\) 满足 \(vc\) 是某个 Lyndon 串的前缀,则对于字符 \(d>c,vd\in L\)。
- 证明:
- 设这个 Lyndon 串为 \(vct\),则 \(\forall i\in[2,len_v],v_{i,len_v}ct>vct\),即 \(v_{i,len_v}c\geq v\),所以 \(v_{i,len_v}d>v_{i,len_v}+c\geq v\),同时因为 \(c\geq v_1\),所以 \(d>c\geq v_1\)。所以 \(vd\in L\)
- 证毕。
1.4 Duval算法
这个算法可以在 \(O(n)\) 时间复杂度,\(O(1)\) 的空间复杂度求出一个串的 Lyndon 分解。
我们只需要维护一个循环不变式。
- \(s_{1,i-1}=s_1s_2...s_g\) 是已经固定下来的分解。
- \(s_{i,k-1}=t^h+v(h\geq1)\) 是没有固定下来的分解,满足 \(t\) 是 Lyndon 串,且 \(v\) 是 \(t\) 的可为空的不等于 \(t\) 的前缀,且有 \(s_g>s_{i,k-1}\)
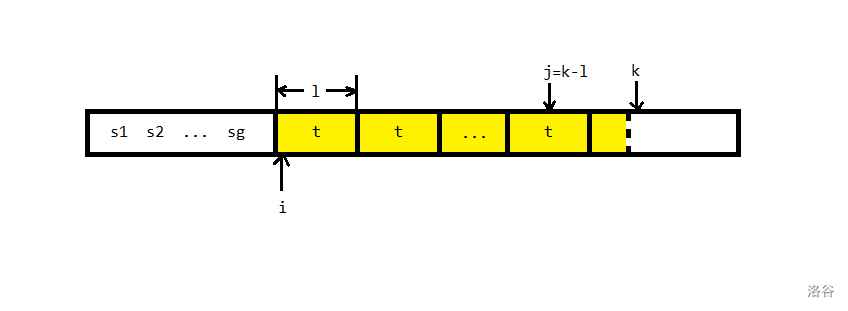
如图片所示。
分三种情况:
- \(s_k=s_j\) 直接往后推。
- 如果 \(s_k>s_j\) ,那么由定理 \(2\) 可以知道 \(v+s_k\) 是 Lyndon 串,由于 Lyndon 分解需要满足的性质,我们需要不断向前合并,让 \(t^h+v+s_k\) 代替 \(t\) ,
- 如果 \(s_j<s_j\) 那么就固定 \(t_h\) 算法从 \(v\) 的开头处开始。
1.5 代码:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ld long double
#define ll long long
#define ull unsigned long long
#define N 5000010
#define M number
using namespace std;
const int INF=0x3f3f3f3f;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
char s[N];
int ans;
int main(){
scanf("%s",s+1);
int len=strlen(s+1);
for(int i=1;i<=len;){
int j=i,k=i+1;
while(k<=len&&s[j]<=s[k]){
if(s[j]<s[k]) j=i;
else j++;
k++;
}
while(i<=j){
ans^=i+k-j-1;
i+=k-j;
}
}
printf("%d\n",ans);
return 0;
}
2 Lyndon分解求解最小表示法
设长度为 \(n\) 的字符串 \(s\),我们对字符串 \(ss\) 求解 Lyndon 分解,我们取左端点在 \(n\) 左边,右端点在 \(n\) 右边的字符串 \(t\),则 \(t\) 的左端点就应该是最小表示法的起点。证明是显然的,只需要想一想 Lyndon 分解的性质即可。
代码要稍微注意一个地方,即如果 \(s\) 是一个循环串,由于题目要求是最前面,所以我们不能再 while 中更新 ans,而应该在循环开头。
2.1代码:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ld long double
#define ll long long
#define ull unsigned long long
#define N 5000010
#define M number
using namespace std;
const int INF=0x3f3f3f3f;
inline int Min(int a,int b){
return a<b?a:b;
}
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n;
char s[N];
int main(){
scanf("%d",&n);
while(n--){
scanf("%s",s);
int len=strlen(s),ans=0;
for(int i=len;i<len*2;i++) s[i]=s[i-len];
len*=2;
for(int i=0;i<len/2;){
ans=i;
int j=i,k=i+1;
while(k<len&&s[j]<=s[k]){
if(s[j]<s[k]) j=i;
else j++;
k++;
}
while(i<=j){
// if(i<len/2&&i+k-j>=len/2) ans=i;
i+=k-j;
}
}
printf("%d\n",ans+1);
}
return 0;
}

