0/1分数规划
1 0/1分数规划
01分数规划是指的下面这个问题。
给定数组a和数组b。要求找到一个x数组,使得:
\[\dfrac{\sum\limits_{i=1}^{n}a_i\times x_i}{\sum\limits_{i=1}^{n}b_i\times x_i}
\]
最大,且\(x_i=0\)或\(1\) \(i\in [1,n]\)。
对 \(1\) 的个数有限制。
2如何求解
设:
\[r=\dfrac{\sum\limits_{i=1}^{n}a_i\times x_i}{\sum\limits_{i=1}^{n}b_i\times x_i}
\]
则有:
\[\sum\limits_{i=1}^{n}a_i\times x_i-r\times\sum\limits_{i=1}^{n}b_i\times x_i=0
\]
我们把这个式子看成一个一次函数,有:
\[f(k)=\sum\limits_{i=1}^{n}a_i\times x_i-k\times\sum\limits_{i=1}^{n}b_i\times x_i
\]
则r为该函数的一个零点。
因为数组a和数组b是给定的。所以x数组控制着这个函数的参数,即不同的x数组会产生不同的函数。
我们知道,该函数的零点,为我们0/1分数规划的一个候选答案。则我们要求的答案就是在这些不同的一次函数中,与x轴截距最大的那个函数的零点。
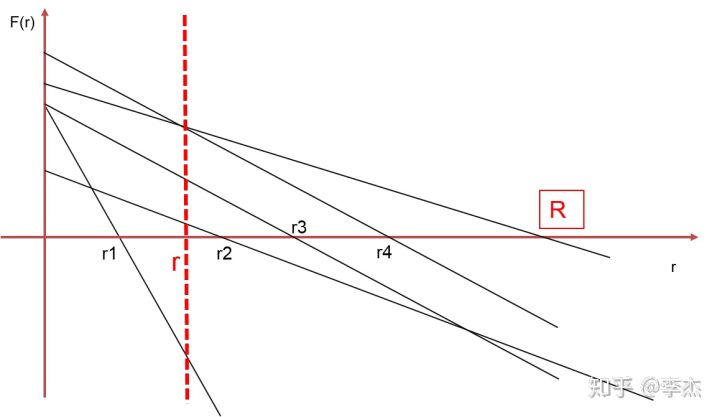
如图。我们要求解的实际上是这个R。
2.1二分
这个显然是可以二分的。具体流程如下:
对于一个mid,求出\(f(mid)_{max}\)来,即在所有的函数与x=mid这条直线的最上方的交点。判断其正负。如果为正,则它右边还有更优的值。如果为负,那最大值应该在左边。
由此二分出结果即可。最大交点函数值对应的x数组明显可以贪心求出。
在有些题目中,可能会限定x中1的个数,设1的个数为q,这个时候我们可以先处理一下所有\(b_i-a_i*mid\),然后选最大的q个即可。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ld long double
#define ll long long
#define ull unsigned long long
#define N 100010
#define M number
using namespace std;
const ld eps=1e-6;
inline ll read(){
ll x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline ll Max(ll a,ll b){
return a>b?a:b;
}
struct rode{
int a,b;
};
rode a[N];
ld b[N];
ll n,m,suma;
struct cmp{
inline bool operator () (ld a,ld b){
return a<b;
}
};
priority_queue<ld,vector<ld>,cmp> q;
inline bool check(ld mid){
ld num=0;
for(int i=1;i<=n;i++) b[i]=(ld)a[i].a-(ld)a[i].b*mid;
nth_element(b+1,b+n-m+1,b+n+1);
for(int i=n;i>=n-m+1;i--) num+=b[i];
if(num>=eps) return 1;
return 0;
}
int main(){
n=read();m=read();
ld l=0,r=0;
for(int i=1;i<=n;i++) a[i].a=read(),suma+=a[i].a;
for(int i=1;i<=n;i++) a[i].b=read();
r=suma;
while(r-l>eps){
ld mid=(r+l)/2;
if(check(mid)) l=mid;
else r=mid;
}
printf("%0.4Lf",l);
return 0;
}
2.2 Dinkelbach算法
本质上是一种迭代法
我们发现,其实二分这种算法对函数值的利用很低。
我们考虑利用函数值。
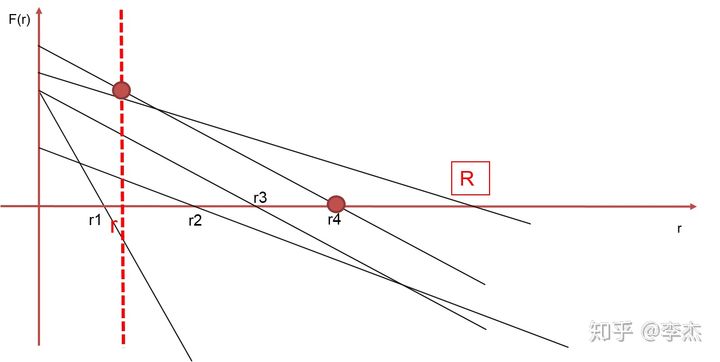
如果我们目前的r非最优,我们把它调整到该函数与x轴的截距上,如图。
一般来说,r的初始值为0。
代码比二分好写一些,LOJ上这个题的数据范围让我头疼于右边界。
代码:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ld long double
#define ll long long
#define ull unsigned long long
#define N 100010
#define M number
using namespace std;
const ld eps=1e-6;
inline ll read(){
ll x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct rode{
int a,b;
ld cha;
inline bool operator < (rode c){
return cha<c.cha;
}
};
rode a[N];
ll n,m,suma;
inline bool solve(ld r,ld &now){
for(int i=1;i<=n;i++) a[i].cha=(ld)a[i].a-(ld)a[i].b*r;
nth_element(a+1,a+n-m+1,a+n+1);
ll suma=0,sumb=0;ld num=0;
for(int i=n;i>=n-m+1;i--){
num+=a[i].cha;
suma+=a[i].a;
sumb+=a[i].b;
}
now=(ld)suma/(ld)sumb;
if(num>eps) return 1;
return 0;
}
int main(){
n=read();m=read();
for(int i=1;i<=n;i++) a[i].a=read(),suma+=a[i].a;
for(int i=1;i<=n;i++) a[i].b=read();
ld r=0,now;
while(solve(r,now)) r=now;
printf("%0.4Lf\n",now);
return 0;
}


