极大子矩阵问题
1悬线法
1.1用途
悬线法是一种求解给定矩阵中的极大矩阵的算法。
所谓“给定矩阵中的极大矩阵”是指一个矩形中有一些障碍点,求内部不包含任何障碍点且边界与坐标轴平行的子矩形。
1.2相关定义 & 定理
我们定义有效子矩形为内部不包含任何障碍点且边界与坐标轴平行的子矩形。
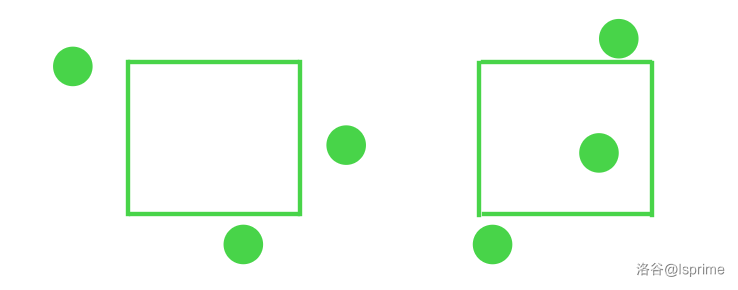
显然图中第一个矩形是有效子矩形而第二个矩形不是。
对于一个有效子矩形,如果不存在包含它且比它大的有效子矩形则称它为极大有效子矩形,而最大有效子矩形为极大有效子矩形中最大的一个(或多个)。
由此我们可以得到定理:一个极大有效子矩形的四条边一定不能向外扩展。也就是说,一个极大有效子矩形的一条边,要么与矩形边界重合,要么往外一格就是障碍点,这个定理的证明很显然,如果有边可以向外扩展,我们要求最大有效子矩形,一定会向外扩展以扩大面积。
1.3悬线法讲解
对于此类问题,我们显然需要一种快速的方法求解(暴力效率极低)。
我们求一个最大有效子矩形,一定是极大有效子矩形中的一个,也就是说,我们可以求所有极大有效子矩形,然后扫描它们,求出面积最大值。
所以现在问题就转变为了求所有的极大有效子矩形。
我们引入悬线的概念。我们称除两个端点外不覆盖任何障碍点的竖直线段为有效竖线,上端点覆盖了一个障碍点或达到整个矩形上端的有效竖线为悬线。
我们可以发现,每一个极大有效子矩形都可以由一条悬线向左右尽可能的移动得到,也就是说,我们只要处理出每条悬线的极大有效子矩形就可以求出所有的极大有效子矩形。
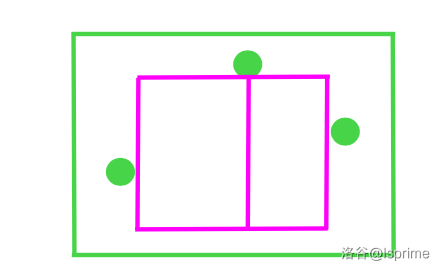
图为将一条悬线左右尽可能移动得到的极大子矩形。
所以,当前问题转化成了处理所有悬线。
容易发现,悬线所有的点都是由其最下面的点决定的,所以我们只要确定了下面的点,整个悬线的长度也就随之确定。我们利用递推来处理。设\(up_{ij}\)表示底部点为(i,j)的悬线长度,初始化是如果这个格子不是障碍,那么其悬线的长度为1,容易写出递推式,如果格子(i,j)和格子(i-1,j)都不是障碍的话,可以知道\(up_{i,j}=up_{i-1,j}+1\)。
代码:
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(!a[i][j]&&!a[i-1][j]) up[i][j]=up[i-1][j]+1;
接下来我们要做的就是处理出所有悬线能左右延伸的最长长度。如果我们知道每个点能左右延伸的最长长度,那么,这个长度的最小值就是悬线能左右延伸的长度。所有我们优先处理每个点所能延伸的最长长度。
我们设\(l_{i,j}\)为点(i,j)能往左延伸的列号,即能向左延伸的最长长度的那一列,或是向左最多能扩展到第几列,容易发现这也是可以递推来完成的。如果格子(i,j)和(i-1,j)都不是障碍,那么就有\(l_{i,j}=l_{i-1,j}\),处理向右延伸的最长长度同理,设\(r_{i,j}\)为该点能向右延伸最多到哪一列,则有\(r_{i,j}=r_{i,j+1}\),同样格子(i,j)(i,j+1)也不是障碍。l、r数组的初始化都是如果该点不是障碍,则值为该点的列号,尤其注意的是,l为从左到有更新,从第2列开始更新,否则第一列数据会被覆盖。r为从右到左更新,从倒数第二列开始更新,否则最后一列数据会被覆盖。
代码:
for(int i=1;i<=n;i++)
for(int j=2;j<=m;j++)
if(!a[i][j]&&!a[i][j-1]) l[i][j]=l[i][j-1];
for(int i=1;i<=n;i++)
for(int j=m-1;j>=1;j--)
if(!a[i][j]&&!a[i][j+1]) r[i][j]=r[i][j+1];
处理完这些之后,我们开始下一步。
在这一步中,我们要同时完成两件事情,1.对l、r数组的合并,统计答案。
枚举顺序是从上到下,从左到右。
在这一步,l和r的定义发生变化,它们不再是表示该点向左(右)最多扩展到哪一列,而是表示以该点为最下面的点的悬线向左(右)最多扩展到哪一列。同样,还可以用递推来实现。因为是最低点,所以只要与上面的点进行合并即可。
代码:
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(i>=2&&!a[i][j]&&!a[i-1][j]){
l[i][j]=Max(l[i][j],l[i-1][j]);
r[i][j]=Min(r[i][j],r[i-1][j]);
}
ans=Max(ans,up[i][j]*(r[i][j]-l[i][j]+1));
}
在递推的同时,要注意i为1是不能更新l和r,否则在没有对第0行初始化的前提下会覆盖答案。如果存在障碍也不能更新。
值得注意的是,虽然第一行不参与递推,但参与统计答案。答案更新的方式就是用悬线的长度乘上它左右能够扩展的最大长度。
1.4代码实现
例题:https://www.luogu.com.cn/problem/P4147
这就是个裸的最大子矩阵面积,选线法完全可以做。代码:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ll long long
#define ld long double
#define ull unsigned long long
#define N 1010
#define M number
using namespace std;
bool a[N][N];
int up[N][N],l[N][N],r[N][N];
int n,m,ans=-1;
inline int Max(int a,int b){
return a>b?a:b;
}
inline int Min(int a,int b){
return a>b?b:a;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
char x;x=getchar();
while(x!='R'&&x!='F') x=getchar();
if(x=='R') a[i][j]=1;
else a[i][j]=0,up[i][j]=1,l[i][j]=r[i][j]=j;
}
for(int i=1;i<=n;i++)
for(int j=2;j<=m;j++)
if(!a[i][j]&&!a[i][j-1]) l[i][j]=l[i][j-1];
for(int i=1;i<=n;i++)
for(int j=m-1;j>=1;j--)
if(!a[i][j]&&!a[i][j+1]) r[i][j]=r[i][j+1];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(!a[i][j]&&!a[i-1][j]) up[i][j]=up[i-1][j]+1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(i>=2&&!a[i][j]&&!a[i-1][j]){
l[i][j]=Max(l[i][j],l[i-1][j]);
r[i][j]=Min(r[i][j],r[i-1][j]);
}
ans=Max(ans,up[i][j]*(r[i][j]-l[i][j]+1));
}
}
printf("%d\n",ans*3);
return 0;
}
根据上面的代码,不难得出悬线法的时间复杂度:O(nm)。
新增加一道例题,这是一种只能用悬线法做的最大子矩阵问题,因为它的障碍点是“不固定的”,对于不同的点来说,障碍点不同,但还是可以在稍稍变形的基础上,用悬线法过掉:
例题:https://www.luogu.com.cn/problem/P1169
代码:(后面有提示)
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ll long long
#define ld long double
#define ull unsigned long long
#define N 2010
#define M number
using namespace std;
int n,m,a[N][N],ans1,ans2;//1: zheng 2.ju
int up[N][N],l[N][N],r[N][N];
inline int Max(int a,int b){
return a>b?a:b;
}
inline int Min(int a,int b){
return a>b?b:a;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
scanf("%d",&a[i][j]);
up[i][j]=1;l[i][j]=r[i][j]=j;
}
for(int i=2;i<=n;i++)
for(int j=1;j<=m;j++)
if(a[i][j]^a[i-1][j]) up[i][j]=up[i-1][j]+1;
for(int i=1;i<=n;i++)
for(int j=2;j<=m;j++)
if(a[i][j]^a[i][j-1]) l[i][j]=l[i][j-1];
for(int i=1;i<=n;i++)
for(int j=m-1;j>=1;j--)
if(a[i][j]^a[i][j+1]) r[i][j]=r[i][j+1];
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
// printf("i:%d j:%d l:%d r:%d\n",i,j,l[i][j],r[i][j]);
if(i!=1&&a[i][j]^a[i-1][j]){
l[i][j]=Max(l[i][j],l[i-1][j]);
r[i][j]=Min(r[i][j],r[i-1][j]);
}
int juli=r[i][j]-l[i][j]+1;
int minn=Min(juli,up[i][j]);
ans1=Max(ans1,minn*minn);
ans2=Max(ans2,juli*up[i][j]);
}
printf("%d\n%d",ans1,ans2);
return 0;
}
这里利用了异或"^"的一个性质,相同则为0,不相同则为1,异或是不进位的加法。
但是,如果n和m很大,但障碍数又很小的情况下,其实我们统计了许多对答案没有贡献的情况。这个答案还不够优。
据说可以用离散化对悬线法进行优化,但是1来我不会用离散化,2来加上离散化后的悬线法(据某些博客上说)还不如用下一种方法:
2扫描法
昨天(2月4号)写的悬线法,今日去找了洛谷上一个题打了一下扫描法,发现这么多Hack数据直接把我吓蒙了。。。据说洛谷加了hack数据后直接卡掉了80%的代码
2.1扫描法讲解
话归正题。因为没有找到写扫描法的好博客(能上日报的那种),所以只能自己敲。(但是图还是可以借一下的)
一下引用一大段文字,看不懂的一些的地方(我认为的)后面会有一些讲解。
算法的思路是这样的,先枚举极大子矩形的左边界,然后从左到右依次扫描每一个障碍点,并不断修改可行的上下边界,从而枚举出所有以这个定点为左边界的极大子矩形。考虑如图2中的三个点,现在我们要确定所有以1号点为左边界的极大矩形。先将1号点右边的点按横坐标排序。然后按从左到右的顺序依次扫描1号点右边的点,同时记录下当前的可行的上下边界。

开始时令当前的上下边界分别为整个矩形的上下边界。然后开始扫描。第一次遇到2号点,以2号点作为右边界,结合当前的上下边界,就得到一个极大子矩形(如图3)。
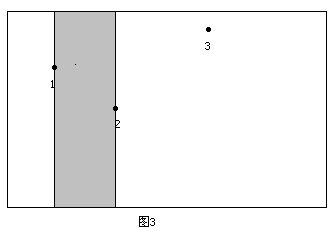
同时,由于所求矩形不能包含2号点,且2号点在1号点的下方,所以需要修改当前的下边界,即以2号点的纵坐标作为新的下边界。第二次遇到3号点,这时以3号点的横坐标作为右边界又可以得到一个满足性质1的矩形(如图4)。4.png类似的,需要相应地修改上边界。以此类推,如果这个点是在当前点(确定左边界的点)上方,则修改上边界;如果在下方,则修改下边界;如果处在同一行,则可中止搜索(因为后面的矩形面积都是0了)。由于已经在障碍点集合中增加了整个矩形右上角和右下角的两个点,所以不会遗漏右边界与整个矩形的右边重合的极大子矩形(如图5)
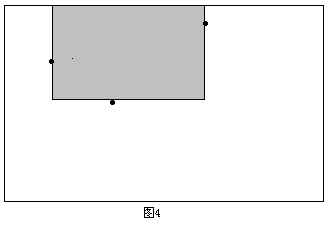
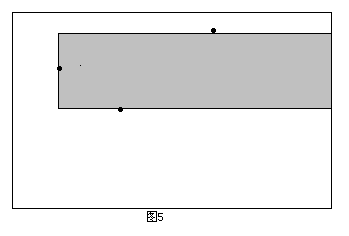
需要注意的是,如果扫描到的点不在当前的上下边界内,那么就不需要对这个点进行处理。
这样做是否将所有的极大子矩形都枚举过了呢?可以发现,这样做只考虑到了左边界覆盖一个点的矩形,因此我们还需要枚举左边界与整个矩形的左边界重合的情况。这还可以分为两类情况。一种是左边界与整个举行的左边界重合,而右边界覆盖了一个障碍点的情况,对于这种情况,可以用类似的方法从右到左扫描每一个点作为右边界的情况。另一种是左右边界均与整个矩形的左右边界重合的情况,对于这类情况我们可以在预处理中完成:先将所有点按纵坐标排序,然后可以得到以相邻两个点的纵坐标为上下边界,左右边界与整个矩形的左右边界重合的矩形,显然这样的矩形也是极大子矩形,因此也需要被枚举到。
通过前面两步,可以枚举出所有的极大子矩形。算法1的时间复杂度是O(S2)。这样,可以解决大多数最大子矩形和相关问题了。
以上文字均引用于:王知昆《浅谈用极大化思想解决最大子矩形问题》
网站:https://www.cnblogs.com/lxyyyy/p/11376224.html
想看论文原版的可以去百度文库上搜,能搜到。值得一提的是,王知昆dalao的代码有锅。
这并不是我的一家之言,洛谷的例题好多人推翻了王知昆大佬的代码。不过这并不重要。
接下来我简单说一说这个代码要注意到的地方。
1.要扫两遍,从左到右一遍,从右到左一遍。
2.值得注意的是,我们枚举的左边这个边界(假设我们现在正在从左往右扫),根据上面的算法讲解,一定是根据,某个障碍点枚举的,这个障碍点一定要在这个边界上,堵住这个边界向左延伸,这也是为什么王知昆同志说道“,如果这个点是在当前点(确定左边界的点)上方,则修改上边界;如果在下方,则修改下边界;”,有可能修改另一个边界更优,但是因为如果你枚举另一条边界,你的左边界上定然没有障碍点来阻碍。所以它可以向左延伸,直到它遇到了另一个障碍点或是碰到了矩形的左边界,但是无论是哪种情况,都会被我们已经枚举到的,或是将要枚举到的,跟现在我们枚举的情况,没有关系。
3.可能有些同学不是很理解,为什么说“如果处在同一行,则可中止搜索(因为后面的矩形面积都是0了)”,其实我也没有理解括号里王知昆的意思,但是这种方法是正确的,我们不妨设想有这样一个在同一行的点,无论我们提下边界,还是更新上边界,我们的左边界在上下边界更新完后,一定不包括障碍点,即使这个障碍点在这个我们枚举的矩阵的左上角或右下角,这个矩阵仍然可以向左继续延伸,从而会被其它情况所枚举。
事实上,个人觉得悬线法比扫描法要简单,而且扫描法细节更多。
2.2代码实现:(后面会有提示)
例题:https://www.luogu.com.cn/problem/P1578
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ll long long
#define ld long double
#define ull unsigned long long
#define N 5010
#define M number
using namespace std;
struct point{
int x,y;
};
point a[N];
int n,m,q,ans;
inline int Min(int a,int b){
return a>b?b:a;
}
inline int Max(int a,int b){
return a>b?a:b;
}
inline bool cmp1(point a,point b){
if(a.x!=b.x) return a.x<b.x;
else return a.y<b.y;
}
inline bool cmp2(point a,point b){
if(a.y!=b.y) return a.y<b.y;
else return a.x<b.x;
}
inline void t_left(int k){
int maxup=0,maxdown=n;
for(int i=k-1;i>=0;i--){
if(a[i].y==a[k].y) continue;
if((a[i].x<=maxup||a[i].x>=maxdown)&&i!=0) continue;
ans=Max(ans,(a[k].y-a[i].y)*(maxdown-maxup));
if(a[i].x==a[k].x) break;
if(a[i].x<a[k].x) maxup=Max(maxup,a[i].x);
else maxdown=Min(maxdown,a[i].x);
}
}
inline void t_right(int k){
int maxup=0,maxdown=n;
for(int i=k+1;i<=q+1;i++){
if(a[i].y==a[k].y) continue;
if((a[i].x<=maxup||a[i].x>=maxdown)&&i!=q+1) continue;
ans=Max(ans,(a[i].y-a[k].y)*(maxdown-maxup));
if(a[i].x==a[k].x) break;
if(a[i].x<a[k].x) maxup=Max(maxup,a[i].x);
else maxdown=Min(maxdown,a[i].x);
}
}
int main(){
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=q;i++) scanf("%d%d",&a[i].x,&a[i].y);
sort(a+1,a+q+1,cmp1);
int maxx=0;
a[0].y=0;a[0].x=0;a[q+1].y=m;a[q+1].x=n;
for(int i=1;i<=q+1;i++) maxx=Max(maxx,a[i].x-a[i-1].x);
ans=maxx*m;
sort(a+1,a+q+1,cmp2);
for(int i=1;i<=q;i++){
t_left(i);
t_right(i);
}
printf("%d\n",ans);
return 0;
}
注意1.要加上两个障碍点:最左上角和最右下角。
原因就是我们枚举每一个点最终都是到了左边界或右边界,所以加上了这两个点,至于这两个点在不在我们极大子矩阵的周围到是无关紧要,在扫描时我们只用到他们的y值,而又给他们加上x值得原因是我们预处理一遍左右边都在左右边界上的最大子矩阵。在排除上下边界以外的点时,一定要注意排除我们新加上去的两个障碍点,毕竟这两个点代表的是边界。


