中国剩余定理（CRT）与扩展中国剩余定理（EXCRT）

以上两种算法都是用于解决现行同余方程组问题，只不过中国剩余定理是扩展中国剩余定理的一个特殊化解法。

1.中国剩余定理

中国剩余定理给出了以下的一元线性同余方程组：

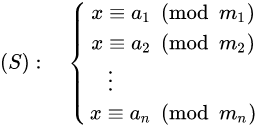
有解的判定条件，并用构造法给出了在有解情况下解的具体形式。
中国剩余定理说明：假设整数\(m_1,m_2, ... ,m_n\)两两互质，则对任意的整数：\(a_1,a_2, ... ,a_n\)，方程组 有解，并且通解可以用如下方式构造得到：
设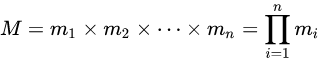是整数\(m_1,m_2, ... ,m_n\)的乘积，并设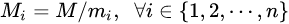是除了mi以外的n- 1个整数的乘积。
设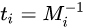则有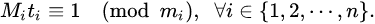
则方程组 的通解形式为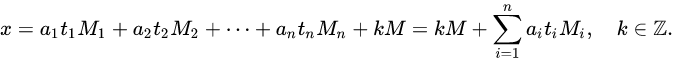
该解在模M的意义下唯一。
如果把该解带入原方程，则发现正确性显然。
代码实现其实是模拟上面的过程，其中求逆元的过程可以用费马小定理和扩展欧几里得，这里博主选用的是扩展欧几里得。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ll long long
#define ull unsigned long long
#define N 11
#define M number
using namespace std;

int n;
ll a[N],b[N],x[N],all=1,ans;

inline ll exgcd(ll a,ll b,ll &x,ll &y){
	if(b==0){
		x=1;
		y=0;
		return a;
	}
	ll gcd=exgcd(b,a%b,x,y);
	ll tmp=x;
	x=y;
	y=tmp-a/b*y;
	return gcd;
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d%d",&a[i],&b[i]),all*=a[i];
	for(int i=1;i<=n;i++){
		ll now=all/a[i];
		ll y;
		ll gcd=exgcd(now,a[i],x[i],y);
		x[i]=(x[i]%a[i]+a[i])%a[i];
//		printf("%d\n",x[i]);
	}
	for(int i=1;i<=n;i++){
		ans+=((all/a[i]*b[i])%all*x[i])%all;
		ans%=all;
	}
	printf("%lld\n",ans);
	return 0;
}

扩展中国剩余定理

运用中国剩余定理的条件是模数两两互素，那么扩展中国剩余定理的使用条件是任意模数。这里给出证明。
对于一个方程组来说，第一个方程的通解很明显能用扩展欧几里得算法得出。
把该解写成通解的形式，带入第二个式子。例如该通解为\(x_0+t*m\)，再带入第二个方程式后，我么要做的是找到一个t使该通解同样满足第二个式子。以此类推。
注意，无论任何时候，该通解在模已经解决的方程的模数的最小公倍数下唯一。代码：（因为long long乘long long可能会溢出，这里用快速乘）

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ll long long
#define ld long double
#define ull unsigned long long
#define N 100100
#define M number
using namespace std;

inline ll exgcd(ll a,ll b,ll &x,ll &y){
	if(b==0){
		x=1;
		y=0;
		return a;
	}
	ll gcd=exgcd(b,a%b,x,y);
	ll tmp=x;
	x=y;
	y=tmp-a/b*y;
	return gcd;
}

ll n;
ll a[N],b[N];

inline ll ksc(ll x,ll y,ll mod){
	ll z=(ld)x/mod*y;
	ll res=(ull)x*y-(ull)mod*z;
	return (res%mod+mod)%mod;
}

int main(){
	scanf("%lld",&n);
	for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i],&b[i]);
	ll m=a[1],x0=b[1];
	for(int i=2;i<=n;i++){
		ll t,q;
		ll g=exgcd(m,a[i],t,q);
		ll now_m=m/g*a[i];
		t=ksc(t,((b[i]-x0)/g+a[i])%a[i],a[i]);
		x0=(x0%now_m+ksc(t,m,now_m))%now_m;
		m=now_m;
	}
	printf("%lld",x0);
	return 0;
}