使用OpenMP与AVX优化矩阵乘法
使用OpenMP与AVX优化矩阵乘法
由于课设内容做的太过简（mo）单（yu），于是在去年12月初的时候就计划写三篇博客随笔作为实验报告，前两篇简单介绍了OpenMP和SIMD指令进行铺垫，本篇将会介绍他的应用场景——优化矩阵乘法。
前两篇的传送门：
1.循环顺序调整
先来看看最基本的矩阵乘法。
void MatrixMul(int **A, int **B, int **C, int size)
{
for (int i = 0; i < size; i++)
for (int j = 0; j < size; j++)
for (int k = 0; k < size; k++)
C[i][j] += A[i][k] * B[k][j];
}
这是一个普通的方阵的乘法函数，用于计算矩阵C = A x B。
线性代数中的矩阵乘法原理告诉我们，只要遵循下面这个原则进行计算就能得到正确结果。
C[i][j] += A[i][k] * B[k][j]
所以，改变循环中ijk的遍历顺序并不会影响结果的正确性。又因为后续使用AVX时需要载入一段连续的内存空间，当前ijk的顺序下最内层循环改变的是k，这就导致B是逐行也就是非连续访问。这既不利于AVX载入数据，也不利于Cache访问。因此我们这里将循环顺序改为ikj，这样就能实现内存的连续访问。
void MatrixMul(int **A, int **B, int **C, int size)
{
// 改为ikj的循环顺序
for (int i = 0; i < size; i++)
for (int k = 0; k < size; k++)
for (int j = 0; j < size; j++)
C[i][j] += A[i][k] * B[k][j];
}
2.使用AVX指令优化
2.1分析
在开始之前，若是不熟悉AVX指令的用法的话，可以先回顾上一篇的内容SSE与AVX指令基础介绍与使用。
在上一步进行调整循环顺序之后，内部已经能够连续访问数据了。现在我们就需要分析，如何用AVX将多次循环合并以提升效率。
for (int j = 0; j < size; j++)
C[i][j] += A[i][k] * B[k][j];
我们可以看到，循环最内层的操作有两步。第一步，将A[i][k]乘上B[k][0]B[k][size-1]。第二部，将第一步乘法的结果加到C[i][0]C[i][size-1]中。
2.2乘法优化
由于最内层循环中A[i][k]并没有改变，所以只需要在循环开始的时候进行一次载入。并且每个数字B[k][j]都是与相同的A[i][k]相乘，所以每个单元都要写入相同的A[i][k]，这就需要使用_mm256_set1_epi32方法进行复制型的加载。
__m256i ra = _mm256_set1_epi32(A[i][k]);
A[i][k]加载完毕后就需要加载B矩阵的内容，这里使用上篇介绍的类型转换就能完成。
// 两种取址方法
__m256i rb = *(__m256i *)(B[k] + j);
__m256i rb = *(__m256i *)(&B[k][j]);
乘法方面注意要使用mullo才能得到每一位相乘的结果。mullo是保存每一个结果的低位，mulhi是保存高位，而mul则是用双倍的空间同时保存低位和高位，这样会导致只能保存一半的乘法结果。
rb = _mm256_mullo_epi32(ra, rb);
2.3加法优化
加法和乘法同理，读取C矩阵的内容。
// 两种取址方法
__m256i rc = *(__m256i *)(C[i] + j);
__m256i rc = *(__m256i *)(&C[i][j]);
和乘法的结果相加。
rc = _mm256_add_epi32(rb, rc);
最后用类型转换的方式写回。
*(__m256i *)(C[i] + j) = rc;
2.4最终结果
AVX一次处理256位数据，也就是8个int，因此循环的步进也需要改为8。另外为了防止越界访问，还需要判断剩余的数据是否大于8个，当内容不足8个时则使用普通的逐个相乘计算。
综上所属，初步的优化结果如下。别忘了32位内存对齐！
void MatrixMul(int **A, int **B, int **C, int size)
{
for (int i = 0; i < size; i++)
for (int k = 0; k < size; k++)
{
int j = 0;
// AVX优化
__m256i ra = _mm256_set1_epi32(A[i][k]);
for (; j <= size - 8; j += 8)
{
// 乘法
__m256i rb = *(__m256i *)(B[k] + j);
rb = _mm256_mullo_epi32(ra, rb);
// 加法
__m256i rc = *(__m256i *)(C[i] + j);
rc = _mm256_add_epi32(rb, rc);
// 写回
*(__m256i *)(C[i] + j) = rc;
}
// 处理余下内容
for(;j<size;j++)
C[i][j] += A[i][k] * B[k][j];
}
}
上面的代码为了表述思路用了很多不必要的中间步骤和变量，为了提高运行效率还能进一步压行简化。
void MatrixMul(int **A, int **B, int **C, int size)
{
for (int i = 0; i < size; i++)
for (int k = 0; k < size; k++)
{
int j = 0;
// AVX优化
__m256i ra = _mm256_set1_epi32(A[i][k]);
for (; j <= size - 8; j += 8)
{
// 简化版
*(__m256i *)(C[i] + j) = _mm256_add_epi32(*(__m256i *)(C[i] + j), _mm256_mullo_epi32(*(__m256i *)(B[k] + j), ra));
}
// 处理余下内容
for (; j < size; j++)
C[i][j] += A[i][k] * B[k][j];
}
}
接下来看看优化前后的性能差距。
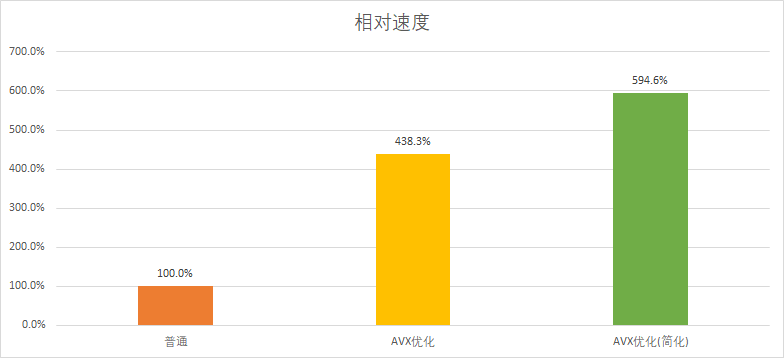
最后得到了近6倍的性能提升，提升幅度还是非常大的。这时候有读者可能会好奇，明明数据吞吐量是原来的8倍，为什么性能却只能提升6倍呢？这其实从简化前后的性能提升也可以看出原因，简化版减少了过程的中间变量，也就是减少了额外的读写开销，但这种开销并不能完全避免，CPU最终还是需要将数据先载入到256位寄存器中计算，然后再从中读取内容写回内存，这种的无法避免额外开销导致了程序始终无法达到8倍的性能提升。
3.使用OpenMP优化
相较于AVX，OpenMP在使用方面就简单了许多，第一篇中我们也对其进行了简单的介绍OpenMP优化for循环的基础运用。
在这里只需要在最外层循环上放加上一句#pragma omp parallel for 即可，当然也可以在末尾加上num_threads(N)设置使用的线程数为N。
void MatrixMul(int **A, int **B, int **C, int size)
{
#pragma omp parallel for num_threads(4) // 设置为4线程
for (int i = 0; i < size; i++)
for (int k = 0; k < size; k++)
for (int j = 0; j < size; j++)
C[i][j] += A[i][k] * B[k][j];
}
接下来我们来测试一下OpenMP在不同线程下的性能变化，测试平台使用的是4C/8T的CPU。
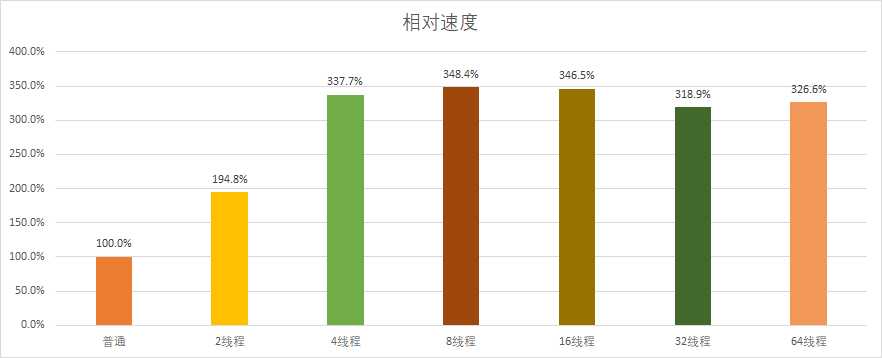
可以看到，OpenMP在2和4线程时性能提升最大，8线程达到顶峰，后续开始出现下降。其中2线程时最接近理论性能提升，到4线程时则开始和理论性能差距拉大。这是由于多线程任务需要系统进行调度，线程调度和开关的损耗会随着则线程数增加而增长，并且当线程数超过物理CPU规模时也无法达到实际的并行效果，从而使提升速度放缓乃至出现下降。
4.综合OpenMP与AVX
在前面分别使用了OpenMP和AVX之后，现在我们来将二者同时运用起来，只需要在AVX的基础上在最外层循环上方加上OpenMP指令即可。
void MatrixMul(int **A, int **B, int **C, int size)
{
#pragma omp parallel for num_threads(4) // OpenMP优化(4线程)
for (int i = 0; i < size; i++)
for (int k = 0; k < size; k++)
{
int j = 0;
// AVX优化
__m256i ra = _mm256_set1_epi32(A[i][k]);
for (; j <= size - 8; j += 8)
{
// 简化版
*(__m256i *)(C[i] + j) = _mm256_add_epi32(*(__m256i *)(C[i] + j), _mm256_mullo_epi32(*(__m256i *)(B[k] + j), ra));
}
// 处理余下内容
for (; j < size; j++)
C[i][j] += A[i][k] * B[k][j];
}
}
然后来看看同时运用上OpenMP和AVX后的性能变化。
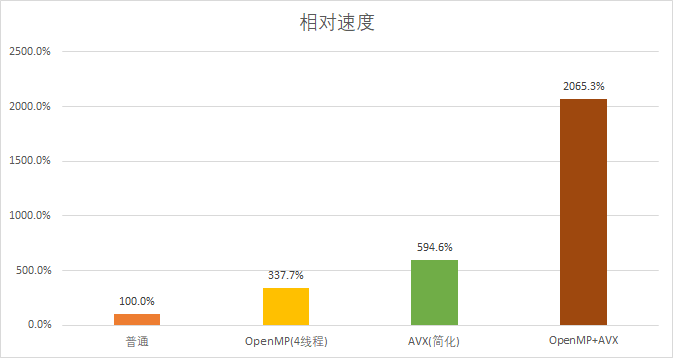
最后的提升基本就是二者实际提升的结果相乘，还是挺理想的。
5.实际应用(图像翻转程序)
最后来看一个实际应用，这里使用的是一个图像翻转程序，实现原理就是先读取图像的rgb值并用矩阵保存，之后再将图像矩阵乘一个转置矩阵实现翻转效果。而本次实验的内容，就是通过加速矩阵乘法的方式加速图像翻转程序。
图像的rgb值分别用3个char矩阵保存，但是由于Intel的SIMD指令集中并没有epi8的乘法指令，所以最低只能使用16位的short数组进行AVX加速，所以本次的AVX优化的for循环步进提升到了一次16个数据。
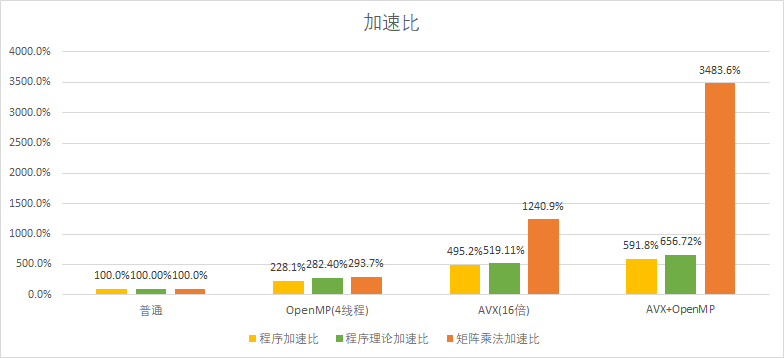
本文发布于2023年1月4日
最后修改于2023年1月4日
