平衡树-Treap
粗谈平衡树(Treap)
平衡树,其实就是对二叉搜索树进行一个优化,防止其退化成链的(优秀)算法。
Treap ?
Treap=Tree+Heap ,顾名思义便是用堆来维护二叉搜索树
我们给二插搜索树上的每个节点随机赋予一个优先级,以此来维护堆,而又因为堆总是一棵完全二叉树,所以防止了二叉搜索树退化成链。
那有没有可能你随机赋予的值正好也使它退化成链呢?有!不过概率特别特别小,如果你脸都这么黑,那你还是退奥信组吧。所以这种情况可以认为是不存在的(相信自己的rp)。
BB
博主认为下面代码注释已经打得很详细了,这里就不啰嗦,但还是得简单的图解一下维护平衡树中左旋和右旋的基本操作。
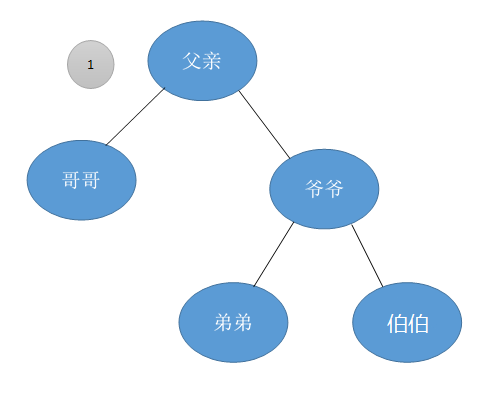
如上图,由于某种不知名的原因,某家族发生了乱伦事件(优先值),作为正义使者,我们要将其进行左旋操作,维护正义!如下:
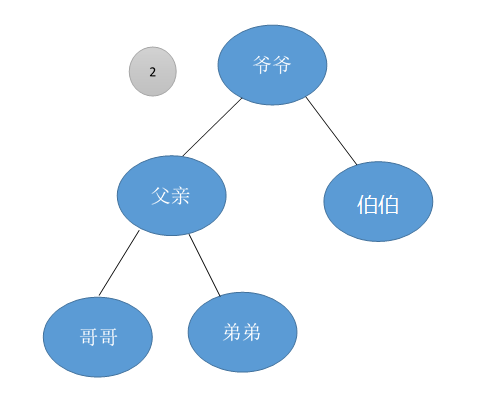
是不是一下就和谐啦!
从中我们可以得出,所谓的左旋操作就是把原本的根节点变为现在根的左节点,然后原本根的右节点变为现在的根,并且把原本根的右节点的左节点作为现在根的左节点的右节点。
后句话很绕,不过很有意思,可以思考一下。后半句换成上图就是将爷爷的左儿子(弟弟)变成成为爷爷新的左儿子(父亲)的新右儿子(乱啊)。
至于右旋操作,就是将上两图,交换一下顺序,原理同理可得。
Code
已经良心打注释了,希望大家食用愉快,不要噎着。
/*Treap-平衡树 by thm date 2019.8.3*/ /*大根堆*/ #include<stdio.h> #include<algorithm> #define INF 2e9 #define MAXN 100010 using namespace std; int n,opt,x; int tot,root/*根*/; struct TREE { int val; //权值 int dat; //优先级 int son[2]; //tree[i].son[0]表示编号为i的节点的左儿子的编号,tree[i].son[1]表示编号为i的节点的右儿子的编号 int size; //子树的大小 int cnt; //与该节点权值相同的副本节点数量 }tree[MAXN]; int New(int v) //创建新结点 { tree[++tot].val=v; tree[tot].dat=rand(); //随机一个优先值 tree[tot].size=1; //新建叶子节点,子树大小为1 tree[tot].cnt=1; //新建节点副本数为1 return tot; //返回新建节点的编号 } void Pushup(int x) { tree[x].size=tree[tree[x].son[0]].size+tree[tree[x].son[1]].size+tree[x].cnt; //同线段树,子树大小=左子树大小+右子树大小+该节点的副本数量 } void Build() //初始化,新建一个最小值和一个最大值 { root=New(-INF); //以极小值为根 tree[root].son[1]=New(INF); Pushup(root); } void Rotate(int &id,int d) //此函数将左旋和右旋并在了一起,d=0表示左旋,d=1表示右旋(注意:此处&id意为引用,很关键) { int temp=tree[id].son[d^1]; tree[id].son[d^1]=tree[temp].son[d]; tree[temp].son[d]=id; id=temp; Pushup(tree[id].son[d]); //更新节点信息 Pushup(id); //同上 }/*此处旋转比较绕,请结合图分析*/ void Insert(int &id,int v) //&id再引用 { if(!id) //如果该处节点为空,则在此处建立新节点 { id=New(v); return; } if(tree[id].val==v) //如果该处节点的权值和插入的权值相同,则将该节点的副本数加一 tree[id].cnt++; else { int d=v>tree[id].val ? 1 : 0; Insert(tree[id].son[d],v); //如果比该节点大则去右区间处理,反之去左区间(与二叉搜索树相同) if(tree[id].dat<tree[tree[id].son[d]].dat) //处理优先值的问题,防止二叉搜索树退化成链 Rotate(id,d^1); //此处因为是维护大根堆,所以如果儿子节点的优先值大于父亲节点,那么就进行旋转操作 } Pushup(id); //更新节点信息 } void Delete(int &id,int v) //&id再再引用 { if(!id) //如果不存在,则直接返回 return; if(tree[id].val==v) //找到 { if(tree[id].cnt>1) //如果副本数量大于1,则副本数量减一 { tree[id].cnt--; Pushup(id); return; } if(tree[id].son[0] || tree[id].son[1]) //如果不大于一,则判断儿子节点的情况 { if(!tree[id].son[0] || tree[tree[id].son[0]].dat<tree[tree[id].son[1]].dat) //如果左儿子为空或者左儿子的优先值小于右儿子的优先值,那么便进行左旋操作 { Rotate(id,0); //左旋 Delete(tree[id].son[0],v); //所要删的节点此时在它父亲节点的左节点上,将其删去就行 } else //没有儿子节点的情况也包含在else里面 { Rotate(id,1); //右旋 Delete(tree[id].son[1],v); //同上,所要删的节点此时在它父亲节点的右节点上,将其删去 } Pushup(id); //更新节点信息 } else id=0; //清除 return; } if(v>tree[id].val) //二叉搜索树的查找操作 Delete(tree[id].son[1],v); else Delete(tree[id].son[0],v); Pushup(id); } int Get_rank(int id,int v) //根据权值找排名 此处不需更改节点,无需引用 { if(!id) //如果不存在,则直接返回 return 0; if(tree[id].val==v) //如果该节点的权值和所查找的权值相同,则排名为左子树的大小加一 return tree[tree[id].son[0]].size+1; if(tree[id].val>v) //如果该节点的权值大于所查找的权值,则去左区间查找 return Get_rank(tree[id].son[0],v); else return tree[tree[id].son[0]].size+tree[id].cnt+Get_rank(tree[id].son[1],v); //如果该节点的权值小于所查找的权值,则排名为左子树的大小加上该节点的副本数量再加上该值在右子树的排名 } int Get_val(int id,int rank) //由排名找值(与Get_rank函数相似) { if(!id) //如果没找到,则返回 return INF; if(rank<=tree[tree[id].son[0]].size) //如果所寻找的排名小于该节点左子树的大小,则该值一定在左区间 return Get_val(tree[id].son[0],rank); if(rank<=tree[tree[id].son[0]].size+tree[id].cnt) //当该排名对应的为该节点或其副本时 return tree[id].val; else return Get_val(tree[id].son[1],rank-tree[tree[id].son[0]].size-tree[id].cnt); //当该排名所对应的值大于该节点的权值时,则去右区间寻找 } int Get_pre(int id,int x) //无更改,不需引用 { int zhi; while(id) //直接通过循环的方式寻找 { if(tree[id].val<x) //如果该节点的值小于所找前驱的值,那么便是要希望所找值越大越好,去右区间区间寻找 zhi=tree[id].val,id=tree[id].son[1]; else //否则去左区间 id=tree[id].son[0]; } return zhi; } int Get_suc(int id,int x) //同Get_pre函数的原理 { int zhi; while(id) { if(tree[id].val>x) zhi=tree[id].val,id=tree[id].son[0]; else id=tree[id].son[1]; } return zhi; } int main() { scanf("%d",&n); Build(); //记得初始化 for(int i=1;i<=n;i++) { scanf("%d%d",&opt,&x); if(opt==1) //插入操作 Insert(root,x); if(opt==2) //删除操作 Delete(root,x); if(opt==3) //查询排名操作 printf("%d\n",Get_rank(root,x)-1); //由于我们初始化插入了一个最大值,so我们查的对应排名应该减一 if(opt==4) //查询对应排名x的数的操作 printf("%d\n",Get_val(root,x+1)); //由于我们初始化插入了一个最小值,so我们查的对应排名的树的真实排名应该为(x+1) if(opt==5) //查询x的对应前驱 printf("%d\n",Get_pre(root,x)); if(opt==6) //查询x的对应后继 printf("%d\n",Get_suc(root,x)); } return 0; }
没错没错以上就是Treap算法180行的代码,怎么?嫌代码长? 那我们来压行一下(嘿嘿)。
压(巨)行(丑)
#include<stdio.h> #include<algorithm> #define INF 2e9 #define MAXN 100010 using namespace std; int n,opt,x,tot,root; struct TREE<%int val,dat,son[2],size,cnt;%>tree[MAXN]; int New(int v) { tree[++tot].val=v; tree[tot].dat=rand(); tree[tot].size=1; tree[tot].cnt=1; return tot; } void Pushup(int x) <%tree[x].size=tree[tree[x].son[0]].size+tree[tree[x].son[1]].size+tree[x].cnt;%> void Build() <%root=New(-INF);tree[root].son[1]=New(INF);Pushup(root);%> void Rotate(int &id,int d) { int temp=tree[id].son[d^1]; tree[id].son[d^1]=tree[temp].son[d],tree[temp].son[d]=id,id=temp; Pushup(tree[id].son[d]);Pushup(id); } void Insert(int &id,int v) { if(!id) <%id=New(v);return;%> if(tree[id].val==v) tree[id].cnt++; else { int d=v>tree[id].val ? 1 : 0; Insert(tree[id].son[d],v); if(tree[id].dat<tree[tree[id].son[d]].dat) Rotate(id,d^1); } Pushup(id); } void Delete(int &id,int v) { if(!id) return; if(tree[id].val==v) { if(tree[id].cnt-->1) <%Pushup(id);return;%> if(tree[id].son[0] || tree[id].son[1]) { if(!tree[id].son[0] || tree[tree[id].son[0]].dat<tree[tree[id].son[1]].dat) <%Rotate(id,0);Delete(tree[id].son[0],v);%> else <%Rotate(id,1);Delete(tree[id].son[1],v);%> Pushup(id); } else id=0; return; } if(v>tree[id].val) Delete(tree[id].son[1],v); else Delete(tree[id].son[0],v); Pushup(id); } int Get_rank(int id,int v) { if(!id) return 0; if(tree[id].val==v) return tree[tree[id].son[0]].size+1; if(tree[id].val>v) return Get_rank(tree[id].son[0],v); else return tree[tree[id].son[0]].size+tree[id].cnt+Get_rank(tree[id].son[1],v); } int Get_val(int id,int rank) { if(!id) return INF; if(rank<=tree[tree[id].son[0]].size) return Get_val(tree[id].son[0],rank); if(rank<=tree[tree[id].son[0]].size+tree[id].cnt) return tree[id].val; else return Get_val(tree[id].son[1],rank-tree[tree[id].son[0]].size-tree[id].cnt); } int Get_pre(int id,int x) { int zhi; while(id) if(tree[id].val<x) zhi=tree[id].val,id=tree[id].son[1]; else id=tree[id].son[0]; return zhi; } int Get_suc(int id,int x) { int zhi; while(id) if(tree[id].val>x) zhi=tree[id].val,id=tree[id].son[0]; else id=tree[id].son[1]; return zhi; } int main() { scanf("%d",&n);Build(); for(int i=1;i<=n;i++) { scanf("%d%d",&opt,&x); if(opt==1) Insert(root,x); if(opt==2) Delete(root,x); if(opt==3) printf("%d\n",Get_rank(root,x)-1); if(opt==4) printf("%d\n",Get_val(root,x+1)); if(opt==5) printf("%d\n",Get_pre(root,x)); if(opt==6) printf("%d\n",Get_suc(root,x)); } return 0; }
这样,我们的平衡树就只有100行啦。
PS:建议初学者手打模板几遍,不要压行!


