[Accumulation Degree]题解

换根dp板子题，首先，我们要想想如果根为1时，1的答案

我们设\(dp[i]\)表示以\(i\)为根子树的中，若\(i\)有无限流量，i点能往下流的最大流量。

我们不难推出式子\(dp[i]=\sum_{v\in son(i)}min(dp[v],w(u->v))\)

意义就是，我们知道一个儿子v可以向下流的最大流量是\(dp[v]\),我们最多可以向儿子v流\(w(u->v)\)的流量，所以我们最多向该儿子流\(min(dp[v],w(u->v))\)的流量，所有儿子的这个值的和就是\(dp[i]\)了

特别的,若i是叶子的话，则\(dp[i]=+oo\)

现在，考虑换根dp

现在，根据换根dp的套路，假设我们要把根\(x\)换成\(x\)的一个儿子\(y\)

那么，我们画一个图：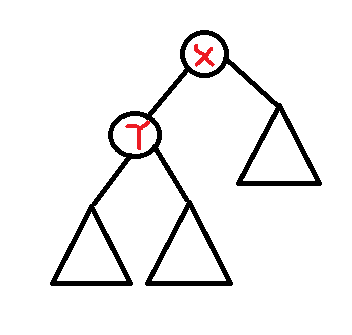

现在我们要把根\(x\)换成\(y\)，图就变成了

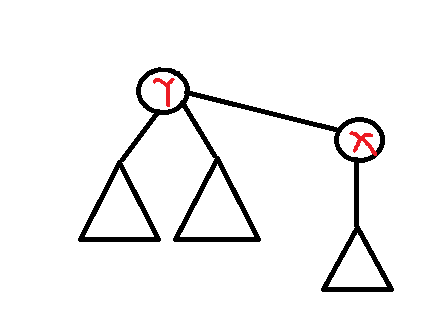
注意到，我们设的dp是，关于\(i\)的子树的，而在换根的过程中，只有\(x\)和\(y\)的子树分别减少和增加了一个儿子，所以，我们只需要将x和y的dp值分别减少和增加变化的值即可将所有的dp值改成以y为根的dp值，即:

\(dp[x]-=min(dp[y],w(x->y))[减去y对x的贡献],dp[y]+=min(dp[x],w(y->x))[加上x对y的贡献]\)【注意，顺序不能反】

同样，我们再考虑下特殊的\(y\)为叶子节点的情况

如果\(y\)是叶子节点，那么图一定是这样：

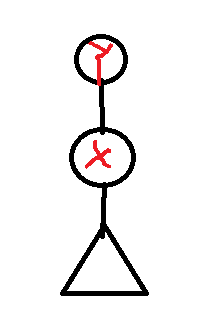
我们发现，这个时候，\(y\)的流量只能流向\(x\)，所以\(y\)对答案的贡献是\(min(dp[x],w(y->x))\),所以，我们只要把这个值和ans取max即可~【因为我们一开始\(dp[y]=+oo\),如果直接算的话会出错】

当然，我们注意到\(dp[x]\)一定会将流量\(w(x->y)\)流向y，所以一定满足此时\(dp[x]>=w(y->x)\)，所以我们直接把\(w(y->x)\)和ans取max即可

至此，我们就成功用\(O(1)\)将根x换成了它的一个儿子y，我们如果直接dfs一遍的话就可以\(O(n)\)求出以任意点为根(源点)时，整个树能流的最大流量，我们直接将答案和这些值取max即可

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+1;
#define int long long
struct node{
    int v,w,nex;
}t[N<<1];
int las[N],len;
int dp[N],ans;
bool flag[N];
inline void add(int u,int v,int w){
    t[++len]=(node){v,w,las[u]},las[u]=len;
}
inline void dfs1(int now,int fa){
    flag[now]=0;
    for(int i=las[now];i;i=t[i].nex){
        int v=t[i].v,w=t[i].w;
        if(v!=fa){
            flag[now]=1;
            dfs1(v,now);
            dp[now]+=min(dp[v],w);
        }
    }
    if(!flag[now]){
        dp[now]=2e9;
    }
}
inline void dfs2(int now,int fa){
    ans=max(ans,dp[now]);
    for(int i=las[now];i;i=t[i].nex){
        int v=t[i].v,w=t[i].w;
        if(v!=fa){
            int pas1=dp[now],pas2=dp[v];//偷懒，直接将原来的值存下来，dfs回来后直接改回去即可
            if(!flag[v]){
                ans=max(ans,w);
                continue;
            }
            dp[now]-=min(dp[v],w);dp[v]+=min(dp[now],w);
            dfs2(v,now);
            dp[now]=pas1,dp[v]=pas2;
        }
    }
}
signed main(){
    int T;
    scanf("%lld",&T);
    while(T--){
        memset(dp,0,sizeof(dp));
        memset(las,0,sizeof(las)),len=0;
        int n;ans=0;
        scanf("%lld",&n);
        for(int i=1;i<n;++i){
            int u,v,w;
            scanf("%lld%lld%lld",&u,&v,&w);
            add(u,v,w),add(v,u,w);
        }
        dfs1(1,1);dfs2(1,1);
        printf("%lld\n",ans);
    }
    return 0;
}