leetcode教程系列——Binary Tree
tree是一种常用的数据结构用来模拟真实物理世界里树的层级结构。每个tree有一个根(root)节点和指向其他节点的叶子(leaf)节点。从graph的角度看,tree也可以看作是有N个节点和N-1个边的有向无环图。
Binary tree是一个最典型的树结构。顾名思义,二分数的每个节点最多有两个children,分别叫左叶子节点与右叶子节点。下面的内容可以让你学习到:
- 理解tree的概念以及binary tree
- 熟悉不同的遍历方法
- 使用递归来解决二分树相关的问题
A. 遍历一棵树
- Pre-order Traversal
- In-order Traversal
- Post-order Traversal
- Recursive or Iterative
1. Pre-order Traversal(前序遍历): 也就是先访问根节点,然后访问左叶子节点与右叶子节点
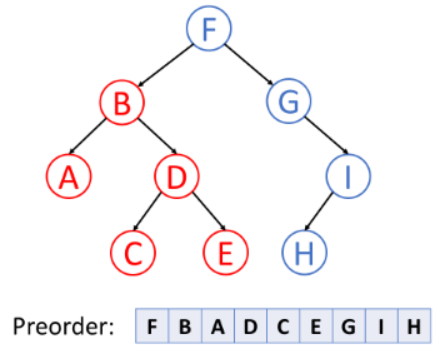
2. In-order Traversal(中序遍历):先访问左叶子节点,接着访问根节点,最后访问右叶子节点
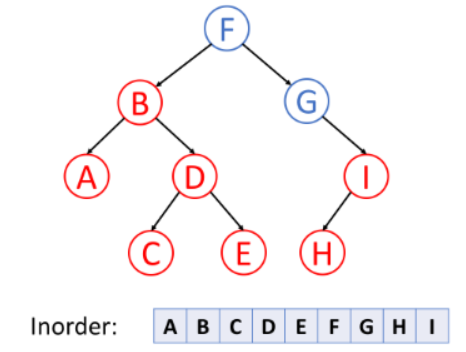
3. Post-order Traversal (后序遍历):先访问左叶子节点,再访问右叶子节点,最后访问根节点
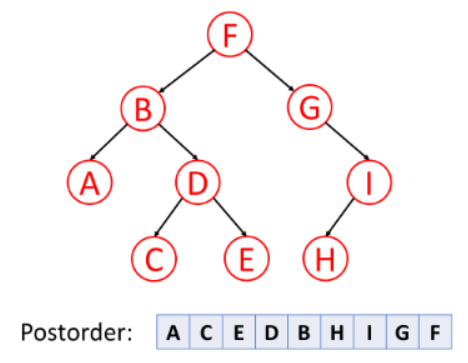
值得注意的是当你删除树的某一个节点时,删除流程应该是post-order(后序)的。也就是说删除一个节点前应该先删除左节点再删除右节点,最后再删除节点本身。
post-order被广泛使用再数学表达式上。比较容易来写程序来解析post-order的表达式,就像下面这种:

使用in-order遍历能够很容易搞清楚原始表达但是不容易处理表达式,因为需要解决运算优先级的问题。
如果使用post-order的话就很容易使用堆栈来解决这个表达。 每个碰到一个运算符的时候就pop两个元素出来计算结果然后再压入栈。
下面来做几个题目:
1.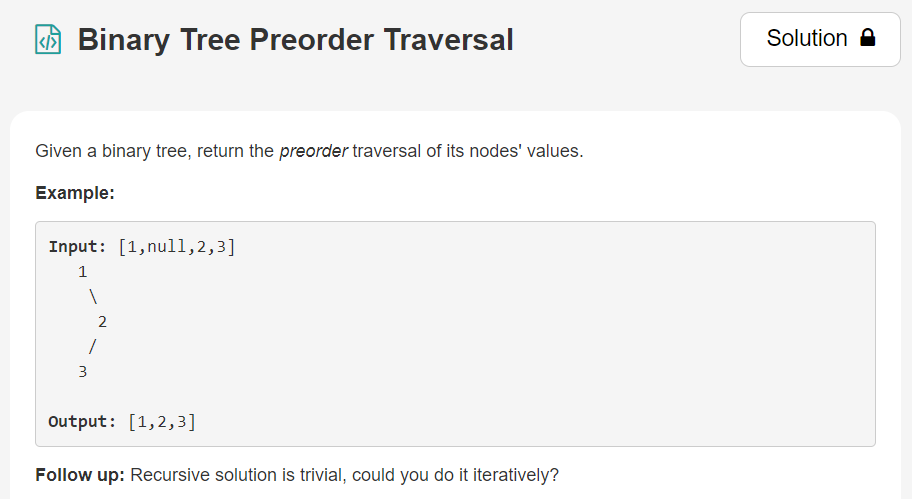
link:[https://leetcode.com/explore/learn/card/data-structure-tree/134/traverse-a-tree/928/]
递归解法:
# Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution(object): def solve(self,root): if root is not None: self.result.append(root.val) self.solve(root.left) self.solve(root.right) return self.result def preorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ self.result=[] self.solve(root) return self.result
循环解法:
# Definition for a binary tree node. # class TreeNode(object): # def __init__(self, x): # self.val = x # self.left = None # self.right = None """ 利用堆栈先进后出的特点 """ class Solution(object): def preorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ result = [] slack = [] if root is not None: slack.append(root) while len(slack)!=0: element = slack.pop() result.append(element.val) if element.right is not None: slack.append(element.right) if element.left is not None: slack.append(element.left) return result
2.
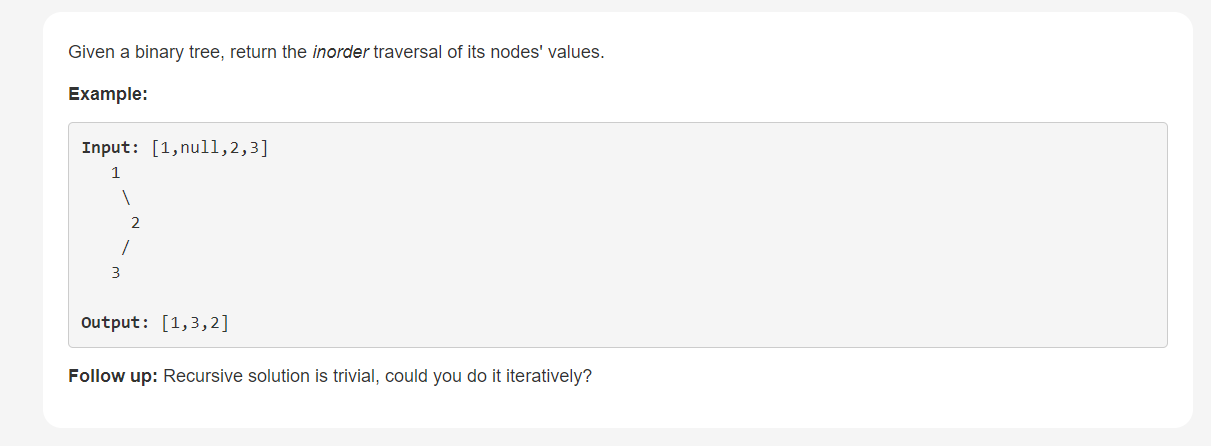
[link]:https://leetcode.com/explore/learn/card/data-structure-tree/134/traverse-a-tree/929/
解题思路:先按照深度遍历左叶子节点压入堆栈,直到没有左叶子节点,就pop该节点将值写入列表,并压入右子节点
class Solution(object): def inorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ slack = [] result = [] cur = None if root is not None: slack.append(root) cur = root.left while(len(slack)>0 or cur is not None): while (cur is not None): slack.append(cur) cur=cur.left element = slack.pop() result.append(element.val) cur = element.right return result
3.

[link]:https://leetcode.com/explore/learn/card/data-structure-tree/134/traverse-a-tree/930/
class Solution(object): def postorderTraversal(self, root): """ :type root: TreeNode :rtype: List[int] """ slack = [] result = [] if root == None: return result pre = None slack.append(root) while (len(slack) != 0): crr = slack.pop() slack.append(crr) if (crr.left == None and crr.right == None) or (pre != None and (pre == crr.left or pre == crr.right)): result.append(crr.val) pre = crr slack.pop() else: if crr.right is not None: slack.append(crr.right) if crr.left is not None: slack.append(crr.left) return result
二分树深度优先搜索:
深度优先搜索顾名思义就是按照树的深度关系一层一层地访问各个节点,如下图所示,一般使用队列先进先出的特点来解决节点的访问顺序问题。
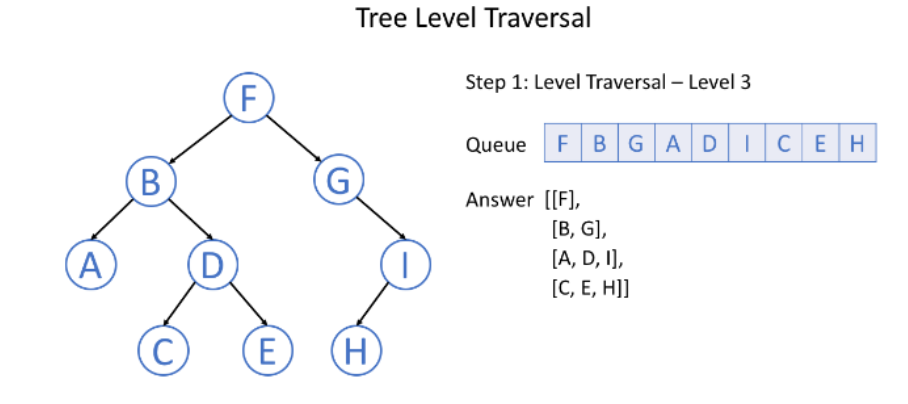
下面来编程实现一个深度遍历问题:
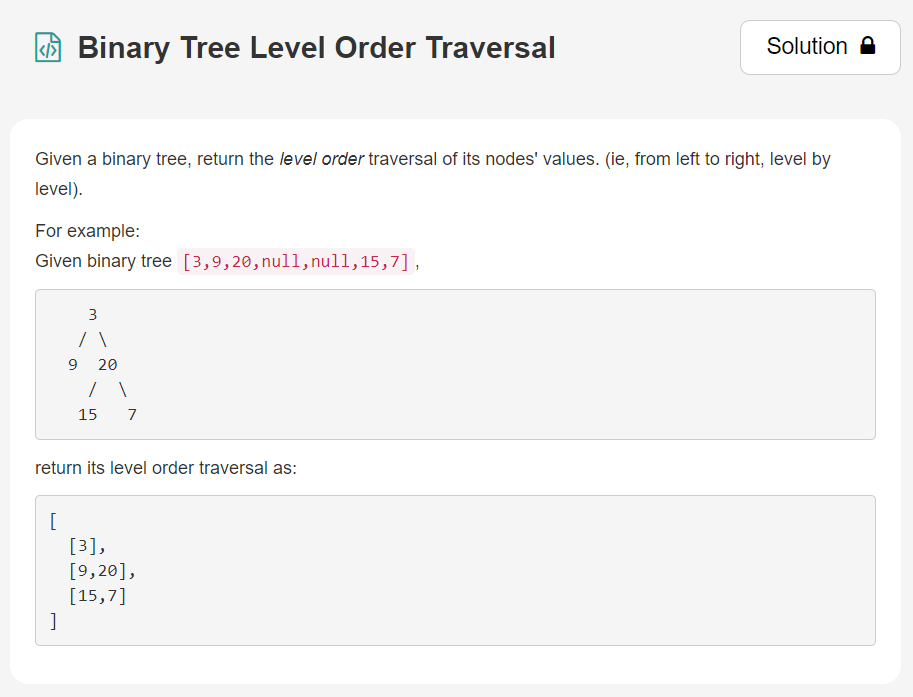
[link]:https://leetcode.com/explore/learn/card/data-structure-tree/134/traverse-a-tree/931/
from queue import Queue class Solution: def levelOrder(self, root: TreeNode) -> List[List[int]]: result = [] q = Queue() if root is None: return result else: q.put([root]) while(q.qsize()!=0): qres = [] vres = [] crrs = q.get() for crr in crrs: vres.append(crr.val) if crr.left!=None: qres.append(crr.left) if crr.right!=None: qres.append(crr.right) result.append(vres) if len(qres)!=0: q.put(qres) return result
下面是一个耗时更少的方法,原理是利用list的pop(0)来实现队列。每次遍历下一级的时候先把当前队列的值都访问完,也就是内循环的工作。
class Solution: def levelOrder(self, root: TreeNode) -> List[List[int]]: result = [] q = [] if root is None: return result else: q.append(root) while(len(q)!=0): res = [] for _ in range(len(q)): crr = q.pop(0) res.append(crr.val) if crr.left != None: q.append(crr.left) if crr.right != None: q.append(crr.right) result.append(res) return result
用递归方法解决Tree问题:
- "Top-down" Solution
- "Bottom-up" Solution
- Conclusion
递归是解决Tree问题时最常见的技术手段。Tree可以被递归定义为一个包含value的根节点加上children节点的引用,所以递归是Tree结构的天然特性,许多关于Tree的问题可以用递归解决。每次调用递归函数时,我们只关注当前节点的问题并递归地解决children。
通常我们可以使用top-down或者bottom方法解决Tree问题。
1. “Top-down”解法:
“Top-down”代表在每个递归调用时,我们首先访问节点获得一些值然后在递归调用时将这些值传递给children。所以“Top-down”解法可以被认为是一种preorder(先序)遍历。具体而言,递归函数top_down(root,params)的工作方式如下所示:
1. return specific value for null node 2. update the answer if needed // answer <-- params 3. left_ans = top_down(root.left, left_params) // left_params <-- root.val, params 4. right_ans = top_down(root.right, right_params) // right_params <-- root.val, params 5. return the answer if needed // answer <-- left_ans, right_ans
例如,考虑下列问题:给顶一个二分树找出最大深度。
我们知道根节点的深度是1。对每个节点,如果我们知道它的深度,我们就知道了它children的深度。因此,如果我们将节点深度当作递归函数的一个参数,那么所有节点都能够知道它们的深度,下面是伪代码。
1. return if root is null 2. if root is a leaf node: 3. answer = max(answer, depth) // update the answer if needed 4. maximum_depth(root.left, depth + 1) // call the function recursively for left child 5. maximum_depth(root.right, depth + 1) // call the function recursively for right child
示意图如下: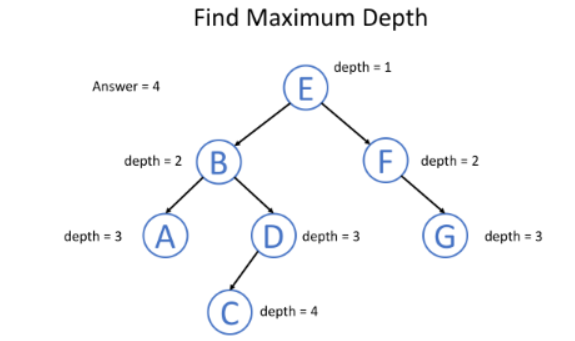
下面是java实现:
private int answer; // don't forget to initialize answer before call maximum_depth private void maximum_depth(TreeNode root, int depth) { if (root == null) { return; } if (root.left == null && root.right == null) { answer = Math.max(answer, depth); } maximum_depth(root.left, depth + 1); maximum_depth(root.right, depth + 1); }
2. "Bottom-up"解法:
“Bottom-up”是另一种递归解法。在每个递归调用时,我们首先对所有的children节点进行递归调用,然后根据该节点本身的值以及返回的值获得结果。这种处理流程可被当作是一种postorder(前序)调用。通常,一个“bottom-up”函数bottom_up(root)如下所示:
1. return specific value for null node 2. left_ans = bottom_up(root.left) // call function recursively for left child 3. right_ans = bottom_up(root.right) // call function recursively for right child 4. return answers // answer <-- left_ans, right_ans, root.val
现在我们用另外一个角度去思考最大深度的问题:对于tree的一个节点,子树在自身处的最大深度x是多少?
如果我们知道它左子树的最大深度$l$与右子树的最大深度$r$,我们是否能解决上述问题?答案是肯定的,我们能够在它们之间选择子树深度的最大值然后加1得到当前节点的深度,也就是$x=max(l,r)+1$。
这表示对于每个节点,我们能够在解决了它的子问题之后得到答案。因此,我们能够使用“bottom-up”解法来解决这个问题。下面是使用“bottom-up”来解决Tree最大深度的伪代码maximum_depth(root):
1. return 0 if root is null // return 0 for null node 2. left_depth = maximum_depth(root.left) 3. right_depth = maximum_depth(root.right) 4. return max(left_depth, right_depth) + 1 // return depth of the subtree rooted at root
下图有一个直观的图例:
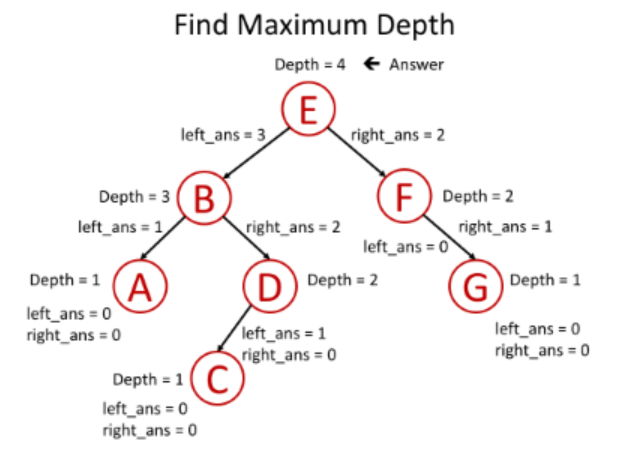
java实现如下:
public int maximum_depth(TreeNode root) { if (root == null) { return 0; // return 0 for null node } int left_depth = maximum_depth(root.left); int right_depth = maximum_depth(root.right); return Math.max(left_depth, right_depth) + 1; // return depth of the subtree rooted at root }
3. Conclusion
理解递归和找出问题的递归解法并不简单,这需要练习。
当你遇到一个tree问题时,问自己两个问题:你能否定义一些参数来帮助节点获得它自身的答案?能否使用这些参数和节点本身的值来决定应该传递什么给它的children。如果这两个问题的答案都是肯定的,使用“top-down”来解决这个问题。
或者你换种方式思考:对于一个树的节点,如果你知道它children的答案,那么是否就能获得这个节点本身的答案?如果答案是肯定的,使用bottom up的方法来解决问题是一个很好的想法。
在下面的章节中,我们提供了几个经典问题来帮助你更好地理解tree结构和递归。
1.最大深度问题
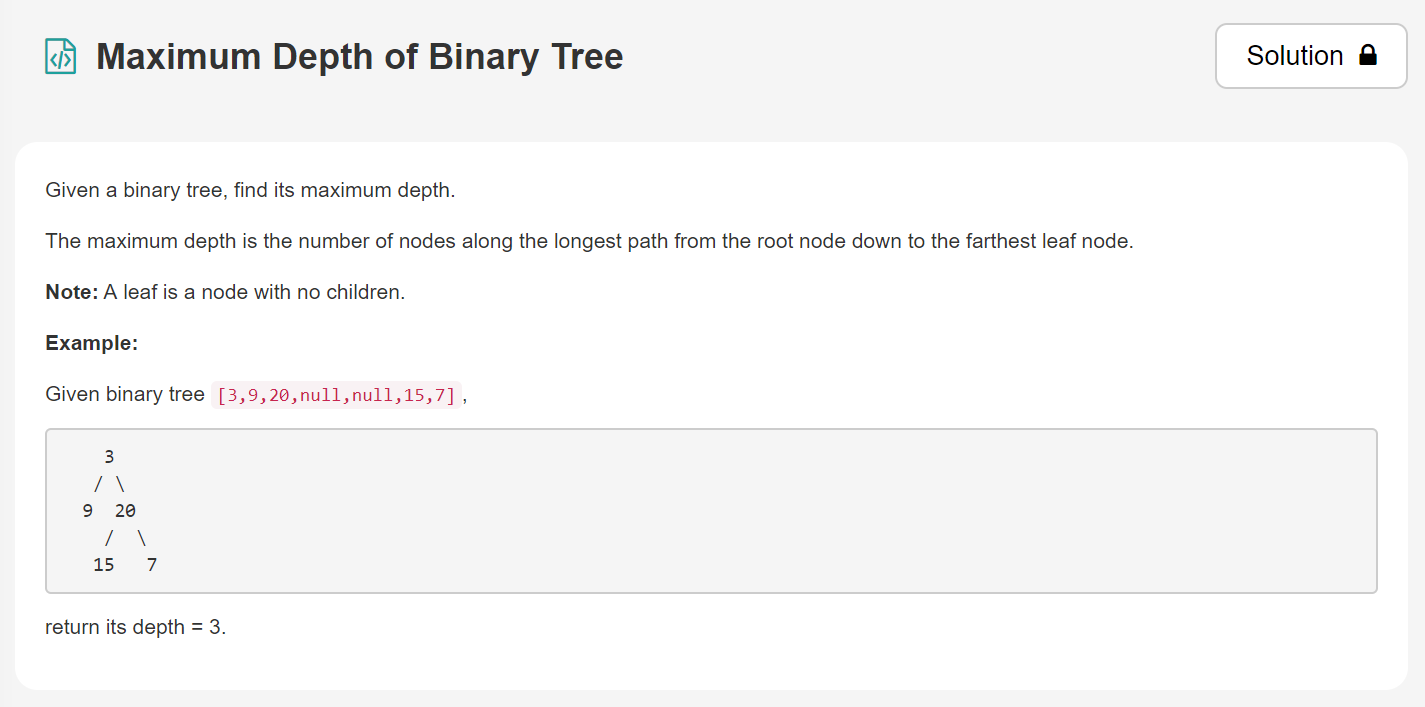
[link]:https://leetcode.com/explore/learn/card/data-structure-tree/17/solve-problems-recursively/535/
class Solution: def maxDepth(self, root: TreeNode) -> int: self.answer = 0 if root is None: return 0 self.maxDepthHelper(root,1) return self.answer def maxDepthHelper(self,node,depth): if node.left is None and node.right is None: self.answer = max(self.answer,depth) if node.left is not None: self.maxDepthHelper(node.left,depth+1) if node.right is not None: self.maxDepthHelper(node.right,depth+1)
2.对称树
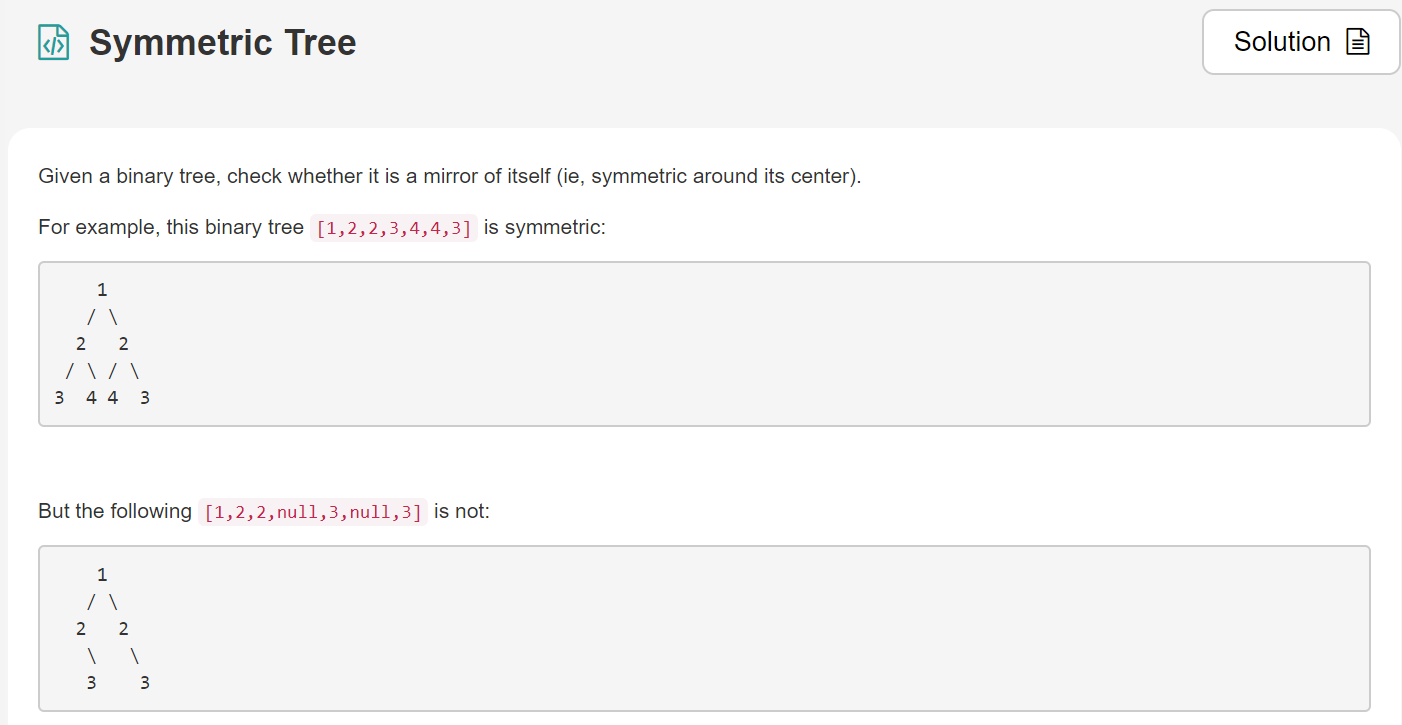
[link]:https://leetcode.com/explore/learn/card/data-structure-tree/17/solve-problems-recursively/536/
递归解法,分成左右子树,如果中途出现了值不相等的情况就立刻返回False,思路如下所示:
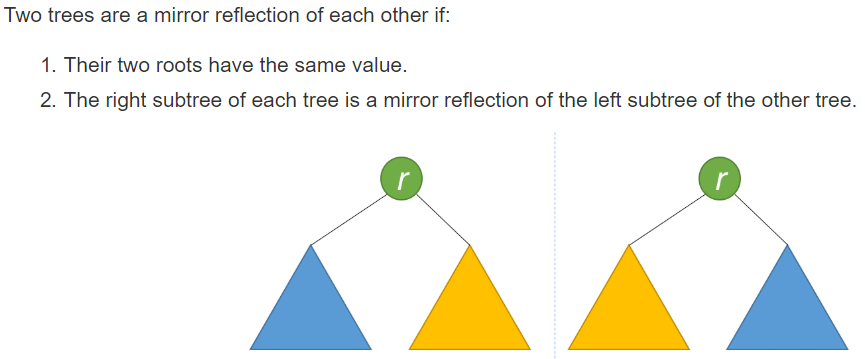
class Solution: def isSymmetric(self, root: TreeNode) -> bool: if root is None: return True return self.helper(root.left,root.right) def helper(self,p,q): if p is None or q is None: return p==q if p.val != q.val: return False return (self.helper(p.left,q.right) and self.helper(p.right,q.left))
循环解法:还是利用堆栈来完成节点访问,碰到不满足的就立刻返回False,否则直至访问完所有节点则返回True
class Solution: def isSymmetric(self, root: TreeNode) -> bool: slack = [] if root is None: return True if root.left is None and root.right is None: return True if root.left is None or root.right is None: return False slack.append(root.left) slack.append(root.right) while(len(slack)>0): left_crr = slack.pop() right_crr = slack.pop() if left_crr is None and right_crr is None: continue if left_crr is None or right_crr is None: return False if left_crr.val != right_crr.val: return False slack.append(left_crr.left) slack.append(right_crr.right) slack.append(left_crr.right) slack.append(right_crr.left) return True
3.路径和

[link]:https://leetcode.com/explore/learn/card/data-structure-tree/17/solve-problems-recursively/537/
解题思路:利用递归思想,如果存在此路径,则当前节点的子树应该存在一条路径等于sum减去目前节点值
class Solution: def hasPathSum(self, root: TreeNode, sum: int) -> bool: if root is None: return False return self.helper(root,sum) is not None def helper(self,node,value): if node is not None: if node.left is None and node.right is None and node.val==value: return True return self.helper(node.left,value-node.val) or self.helper(node.right,value-node.val)
4.由中序遍历和后序遍历构建二叉树
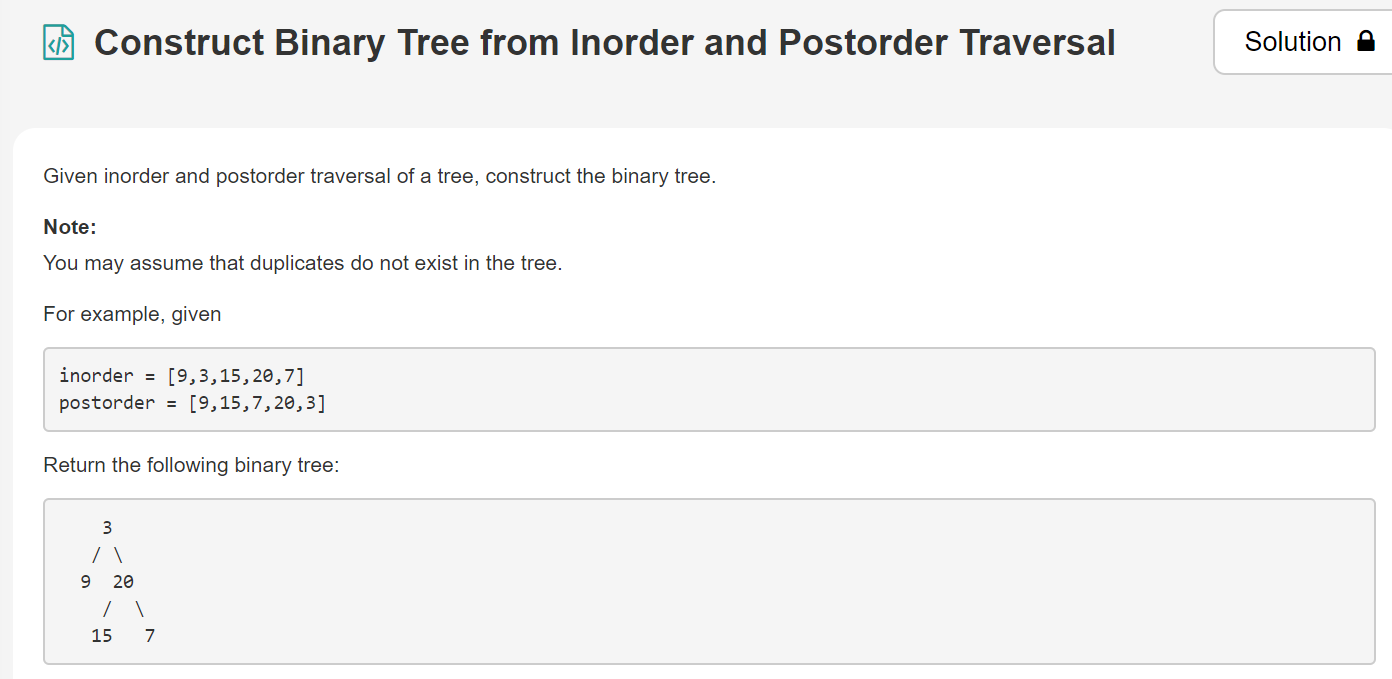
[link]:https://leetcode.com/explore/learn/card/data-structure-tree/133/conclusion/942/
解题思路:后序遍历的最后一个元素一定是根节点,按照这个特性就可以在中序遍历中找出根节点的索引,中序列表中索引左右两边也就是左子树和右子树元素。同理后序列表中索引左边的一定是左子树对应的后序列表,右边是右子树对应的后序列表(以上索引其实代表的是左子树元素的个数,所以后序列表中按照这一个数即可切片分为左子树和右子树)。
class Solution: def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode: if len(inorder)==0 or len(postorder)==0: return None root_val = postorder[-1] root = TreeNode(root_val) index = inorder.index(root_val) root.left = self.buildTree(inorder[:index],postorder[:index]) root.right = self.buildTree(inorder[index+1:],postorder[index:-1]) return root
5.由先序遍历和中序遍历构建二叉树
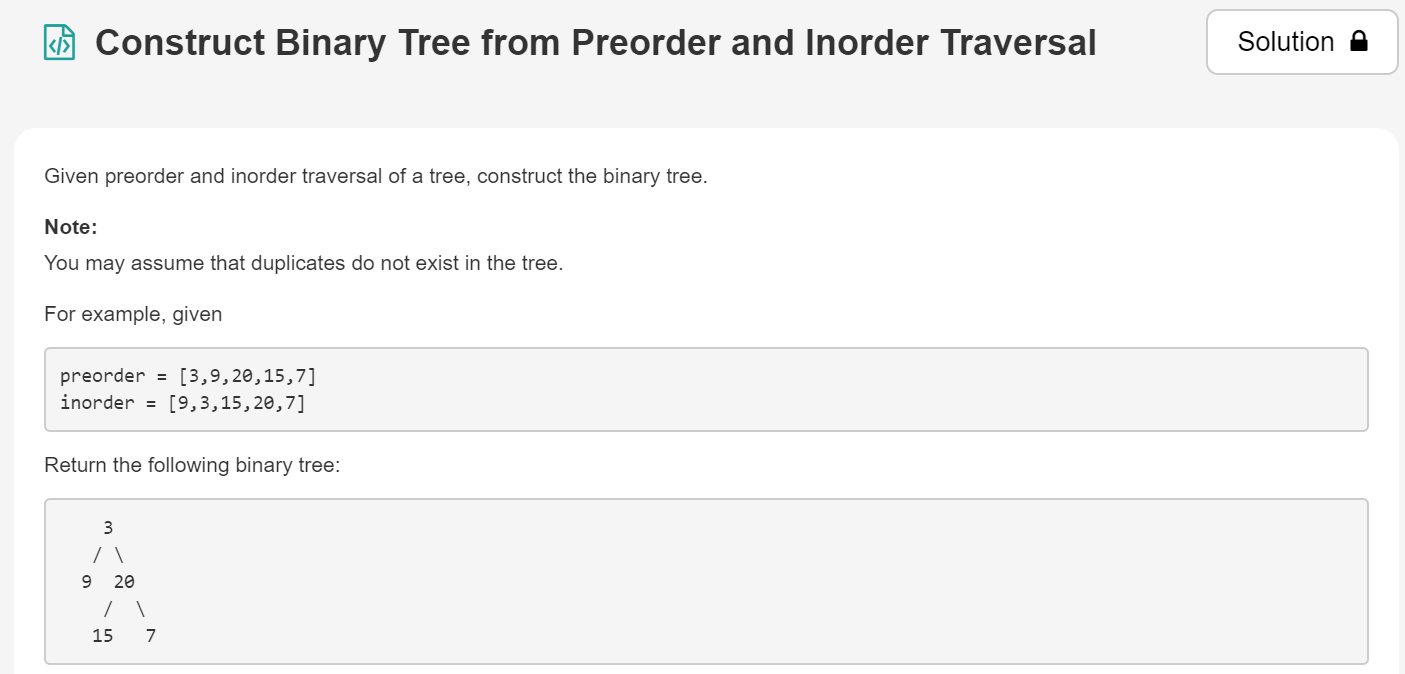
[link]: https://leetcode.com/explore/learn/card/data-structure-tree/133/conclusion/943/
解题思路:先序遍历的第一个元素一定是根节点,然后按照根元素在中序遍历中的索引位置可以获得根元素的左右子树元素数目,然后递归地构造树
class Solution: def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode: if len(preorder)==0 or len(inorder)==0: return None root_val = preorder[0] root = TreeNode(root_val) index = inorder.index(root_val) root.left = self.buildTree(preorder[1:index+1],inorder[:index]) root.right = self.buildTree(preorder[index+1:],inorder[index+1:]) return root
6.在每个节点中填充下一个右指针
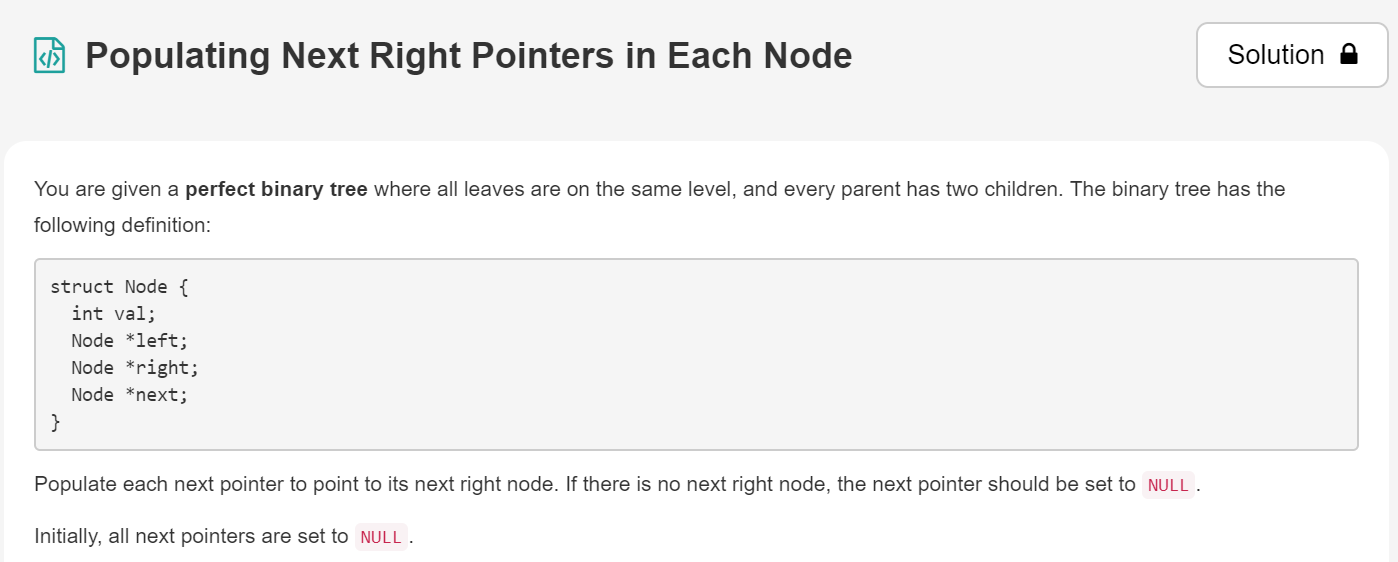

[link]:https://leetcode.com/explore/learn/card/data-structure-tree/133/conclusion/994/
class Solution: def connect(self, root: 'Node') -> 'Node': if root is None: return self.helper(root.left,root.right) return root def helper(self,l_node,r_node): if l_node is None or r_node is None: return l_node.next = r_node self.helper(l_node.left,l_node.right) self.helper(l_node.right,r_node.left) self.helper(r_node.left,r_node.right)
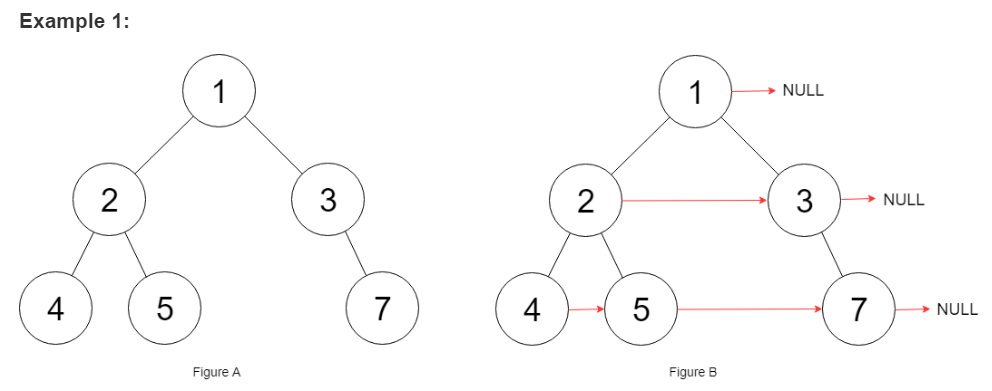
7.在每个节点中填充下一个右指针II
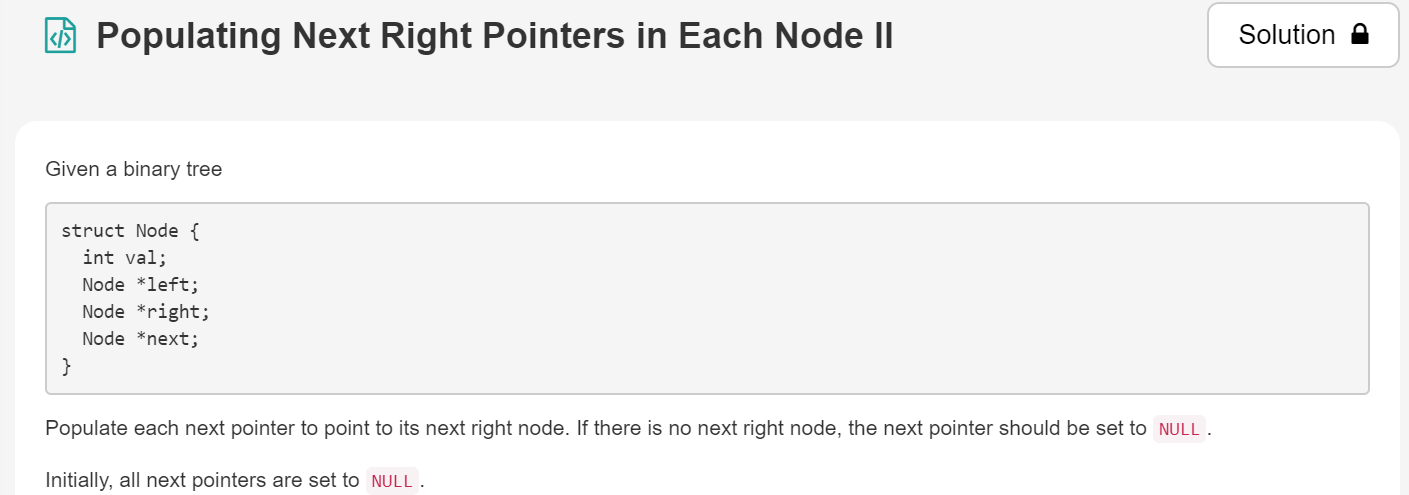
[link]:https://leetcode.com/explore/learn/card/data-structure-tree/133/conclusion/1016/
解题思路:对该树进行广度优先搜索,把访问后的同一级元素按照访问顺序存储在一个队列中,并且设定一个值len来表示同一级元素个数,然后做同级的元素相连操作并且递减len,当len为0时,表示当前层元素处理完了,把len置为当前队列长度,也就是下一级元素个数。
class Solution: def connect(self, root: 'Node') -> 'Node': if root is None: return q = [] q.append(root) length = 1 while(len(q)!= 0): length -= 1 node = q[0] del q[0] if node.left is not None: q.append(node.left) if node.right is not None: q.append(node.right) if length > 0: node.next = q[0] else: length = len(q) return root
8. 最近祖先

[link]: https://leetcode.com/explore/learn/card/data-structure-tree/133/conclusion/932/
解题思路:可以为访问的每个节点增加一个父节点指针,然后根据这一指针找出p和q的父亲节点,依次往上得到父亲节点列表,两个列表的首个共同元素即为p和q的最低祖先。
class Solution: def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode': ls = [] result = [] ls.append(root) root.father=None ready0 = False ready1 = False answer = {} while (len(ls) != 0 and not(ready0 and ready1)): node = ls[0] del ls[0] result.append(node.val) if node.left is not None: ls.append(node.left) node.left.father = node if node.left.val == p.val: ready0 = True p.father = node if node.left.val == q.val: ready1 = True q.father = node if node.right is not None: ls.append(node.right) node.right.father = node if node.right.val == p.val: ready0 = True p.father = node if node.right.val == q.val: ready1 = True q.father = node list1=[p.val] while(p.father): list1.append(p.father.val) p=p.father list2=[q.val] while(q.father): list2.append(q.father.val) q = q.father c = [x for x in list1 if x in list2] return TreeNode(c[0])
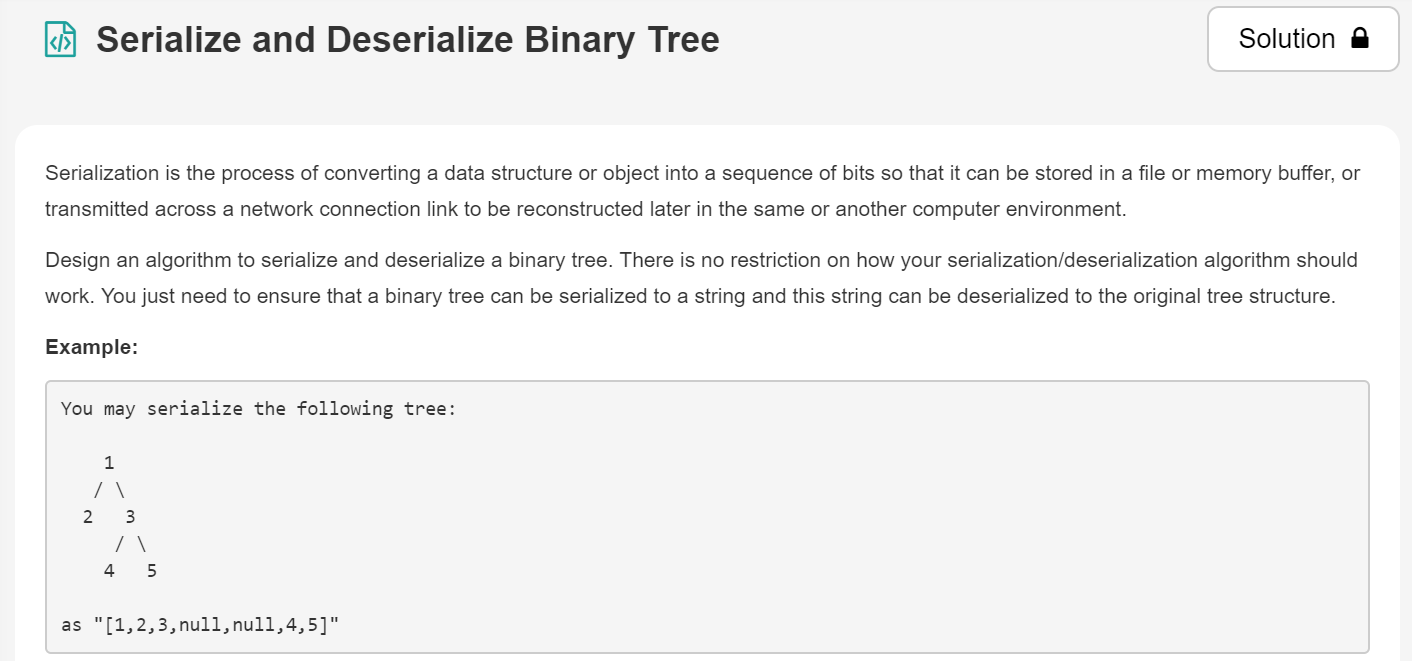
9.二叉树的序列化与反序列化
[link]:https://leetcode.com/explore/learn/card/data-structure-tree/133/conclusion/995/
解题思路:这题比较自由,因为他不要求序列化的具体格式,所以每个人可能都可以按照自己规定的格式编写代码。我的序列化方法比较直白,就是使用逐行扫描添加元素到列表,以上图为例,序列化结果为:[1,2,3,null,null,4,5,null,null,null,null]。反序列化就是提取出一个根节点,其后面两个就分别是左子树与右子树。其实如果你对前面内容比较熟悉,就知道还可以使用先序遍历+中序遍历,后者后序遍历+中序遍历来反序列化。
class Codec: def serialize(self, root): """Encodes a tree to a single string. :type root: TreeNode :rtype: str """ if root is None: return None q = [root] result = [root.val] while(len(q) != 0): node = q[0] del q[0] if node.left is not None: result.append(node.left.val) q.append(node.left) else: result.append("null") if node.right is not None: result.append(node.right.val) q.append(node.right) else: result.append("null") print(result) return result def deserialize(self, data): """Decodes your encoded data to tree. :type data: str :rtype: TreeNode """ if data is None: return None is_Frist = True q = [TreeNode(data[0])] del data[0] while(len(q)!=0): node = q[0] del q[0] if is_Frist: root = node is_Frist = False if data[0] is not "null": left = TreeNode(data[0]) q.append(left) else: left = None if data[1] is not "null": right = TreeNode(data[1]) q.append(right) else: right = None node.left = left node.right = right del data[0] del data[0] return root
恭喜!!到这里leetcode官方教程的所有内容完结,希望你和我一样有所收获!休息一下,我们进入到下一节吧。



