《Domain Agnostic Learning with Disentangled Representations》ICML 2019

　　这篇文章是ICML 2019上一篇做域适应的文章，无监督域适应研究的问题是如何把源域上训练的模型结合无lable的目标域数据使得该模型在目标域上有良好的表现。之前的研究都有个假设，就是数据来自哪个域是有着域标签的，其实这不太现实，就拿手写字识别打比方，不同的人使用不同的笔如纸张，那写出来的字会是不同的域的，识别的时候不可能模型还得需要知道待识别的字来自哪个域。这篇文章研究的内容是如何把有标注的源域信息迁移到无标注的任意目标域数据上。相当于是从1个源域到N个目标域的迁移，而一些之前的论文的假设是目标域数据都是从同一个分布采样的，所以它们的设定为1个源域到1个目标域，与这篇文章考虑的场景不同。

　　这个问题存在两个难点：1)目标数据来自混合的目标域，所以目前主流的特征对齐方法不太适用，2）类无关信息会导致负迁移，特别是当目标域高度异构的时候。为了解决这个问题，作者设计了一个深层对抗解耦自编码器（DADA）来从类标识中解耦出类特定的特征。作者的想法是一个域无关模型的学习不仅仅应该学习源域和目标域之间的不变性内容，它还应该从图像的剩余信息中分离出特定类的特征。

　　目前也有一些通过对抗训练从自编码器的隐空间进行特征解耦的工作，但是将他们用在这种1->N的场景下还是有点问题的。一是这些模型仅仅将隐藏层嵌入解耦为域不变特征和域特定特征(比如天气等)，然后将后者丢掉，没有显示的考虑分离类相关特征和类无关特征(比如背景等)。其次就是这些方法不能保证域不变特征和域特定特征的完全分离。下面来看看作者的解决方案。

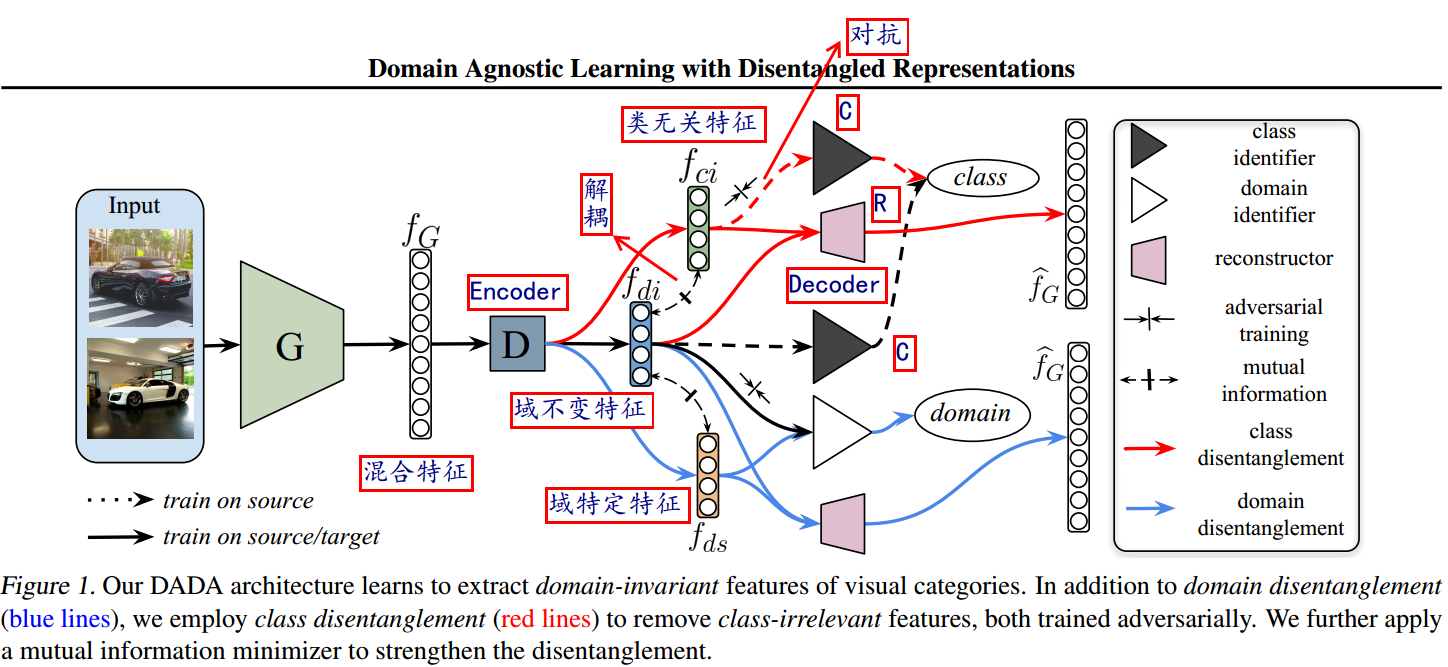
 　　如上图所示，特征生成器$G$将输入图片映射到特征向量$f_{G}$，这个$f_{G}$是一个高度耦合的特征，所以后面编码器$D$的目的是将这个特征解耦为域不变特征$f_{di}$,域特定特征$f_{ds}$和类无关特征$f_{ci}$。特征重建器$R$的目的是接受($f_{di}$,$f_{ci}$)或($f_{di}$,$f_{ds}$)作为输入，然后重建出$f_{G}$。$D$和$R$使用VAE中的编码器与解码器实现。为了强调解耦，在($f_{di}$,$f_{ci}$)以及($f_{di}$,$f_{ds}$)上进行互信息最小化约束。在域判别器支路（白三角）通过对抗训练学习出域不变特征$f_{di}$。类判别器$C$（黑三角）通过在有标注的源域数据上预测类分布$f_{C}$训练得到，类无关特征$f_{ci}$是通过结合$C$以对抗的方式提取到的。

　　下面就来看看每个部件的具体实现：

　　1)Variational Autoencoders：VAE是一种同时训练概率编码器与解码器的深度生成模型。编码器会生成符合高斯分布的隐藏向量。在这篇文章里就是通过使用VAE来获得每个部分的解耦表示，损失函数设计如下：

$\mathcal{L}_{v a e}=\left\|\widehat{f}_{G}-f_{G}\right\|_{F}^{2}+K L\left(q\left(z | f_{G}\right) \| p(z)\right)$

这个式子前一项的目的是重建$G$提取的原始特征，后面一项是惩罚隐藏特征分布与先验分布$p(z_{c})$($z \sim \mathcal{N}(0, I)$)的偏差。这个约束仅仅是将隐藏特征映射到一个标准分布，并没有保证特征解耦。

 

　　2)Class Disentanglement：为了解决上面的问题，这里通过对抗的方式实现类别信息解耦来移除一些类别无关的特征，比如背景等。

首先通过源域数据进行有监督训练得到类判别器$C$：

$\mathcal{L}_{c e}=-\mathbb{E}_{\left(x_{s}, y_{s}\right) \sim \widehat{\mathcal{D}}_{s}} \sum_{k=1}^{K} \mathbb{1}\left[k=y_{s}\right] \log \left(C\left(f_{D}\right)\right)$

这里的$f_{D} \in\left\{f_{d i}, f_{c i}\right\}$。

然后我们固定住类判别器$C$来训练解耦器$D$来生成类无关特征$f_{c_i}$来欺骗$C$。这可以通过最小化预测类分布的负交叉熵来实现：

$\mathcal{L}_{e n t}=-\frac{1}{n_{s}} \sum_{j=1}^{n_{s}} \log C\left(f_{c i}^{j}\right)-\frac{1}{n_{t}} \sum_{j=1}^{n_{t}} \log C\left(f_{c i}^{j}\right)$

这里的第一项与第二项分别指的是在源域上和目标域上的交叉熵最小。

 

　　3)Domain Disentanglement：为了处理域不变性的任务，解耦出类无关特征还不够，因为它还没有让源域和目标域对齐。为了实现更好的对齐，我们进一步提出把学到的特征解耦为域特定特征和域不变特征，然后在域不变隐空间实现源域和目标域的对齐。这通过在得到的隐空间里进行对抗性域判别得到。这里的域判别器叫做$DI$，它接收解耦的特征（$f_{di}$或$f_{ds}$）作为输入，输出域标签$l_f$(源域或者目标域)。这一块的损失函数为：

$\mathcal{L}_{D I}=-\mathbb{E}\left[l_{f} \log P\left(l_{f}\right)\right]+\mathbb{E}\left(1-l_{f}\right)\left[\log P\left(1-l_{f}\right)\right]$

之后就训练解耦器$D$来欺骗域判别器$DI$来提取域不变特征。

 

 　　4) Mutual Information Minimization：为了更好地解耦特征，我们最小化域不变特征$f_{di}$和域无关特征$f_{ds}$之间的互信息，以及域不变特征$f_{di}$和类无关特征$f_{ci}$之间的互信息：

$I\left(\mathcal{D}_{x} ; \mathcal{D}_{f_{d i}}\right)=\int_{\mathbb{X} \times \mathcal{Z}} \log \frac{d \mathbb{P}_{X Z}}{d \mathbb{P}_{X} \otimes \mathbb{P}_{Z}} d \mathbb{P}_{X Z}$

上式子就是互信息的定义，具体可以查看百度百科。这里的$x \in\left\{f_{d s}, f_{c i}\right\}$，$\mathbb{P}_{X Z}$是$\left(\mathcal{D}_{x}, \mathcal{D}_{f_{d i}}\right)$的联合分布，$\mathbb{P}_{X}=\int_{Z} d \mathbb{P}_{X Z}$和$\mathbb{P}_{Z}=\int_{X} d \mathbb{P}_{X Z}$是边缘分布。尽管互信息是跨领域的关键度量，但它只适用于离散变量或有限的概率分布未知的问题。而且计算复杂度为$O\left(n^{2}\right)$，不适合深层的CNN。因此这篇文章采用的是互信息神经估计器(MINE):

$\widehat{I(X ; Z)_{n}}=\sup _{\theta \in \Theta} \mathbb{E}_{\mathbb{P}_{X Z}^{(n)}}\left[T_{\theta}\right]-\log \left(\mathbb{E}_{\mathbb{P}_{X}^{(n)} \otimes \widehat{\mathbb{P}}_{Z}^{(n)}}\left[e^{T_{\theta}}\right]\right)$

 

　　5) Ring-style Normalization:传统的Batch Normalization通过减去批均值并除以批标准差来减小内部协变量偏移。尽管在领域自适应方面取得了很好的结果，但是单靠BN还不足以保证嵌入的特征在不同域的场景中得到很好的标准化。因为我们的目标域数据来自多个域的采样，并且它们的嵌入特征不规则地分散在隐空间中。18年郑等(2018)提出了一种环形规范约束，以保持多个类的角分类边界之间的平衡，如下：

$\mathcal{L}_{r i n g}=\frac{1}{2 n} \sum_{i=1}^{n}\left(\left\|T\left(x_{i}\right)\right\|_{2}-R\right)^{2}$

这里的R是学习到的norm值。但是$ring loss$是不鲁棒的，如果学习的R很小，可能会导致模式崩溃(mode collapse)。我们把ring loss整合到一个$Geman-McClure$模型并最小化下面的损失函数：

$\mathcal{L}_{\text {ring}}^{G M}=\frac{\sum_{i=1}^{n}\left(\left\|T\left(x_{i}\right)\right\|_{2}-R\right)^{2}}{2 n \beta+\sum_{i=1}^{n}\left(\left\|T\left(x_{i}\right)\right\|_{2}-R\right)^{2}}$

这里$\beta$是$Geman-McClure$模型的比例因子。

 

Optimization：我们的模型是以端到端的方式训练的。我们使用随机梯度下降或Adam优化器迭代地训练类和域解耦组件、MINE和重构组件。我们使用流行的神经网络(如LeNet、AlexNet或ResNet)作为我们的特征生成器$G$。