Unsupervised Person Re-identification by Soft Multilabel Learning
简介:
这是一篇19年CVPR的跨域无监督Re-ID论文,在Market1501和DukeMTMC-reID上分别达到了67.7%和67.1%的rank-1精度,算是一篇将准确度刷得比较高的论文了,在这篇论文中主要是偏重了loss函数的设计而非网络结构,所以理解起来还是有一定难度的,下面就来一探它的奥秘。
主要工作:
- 在对无标注的目标域数据打伪标签时不适用onehot这样的硬值,而是将目标域无标签人物身份表示为与一组额外数据集中已知标签人物的相似度(软多标签),这篇论文将额外数据集(类似源域的概念)的有标签行人叫做参考人物
- 利用外观特征与软多标签之间的一致性进行困难负样本挖掘
- 因为行人重识别的一个setting是跨摄像头匹配,所以引入了约束来保持软多标签在不同视角相机下保持一致性
- 引入参考代理学习来将每一个代理人在联合嵌入中表示为一个参考代理
方法:
下面就来看看作者是怎么来实现他说的这几点
1.问题定义
我们有目标数据集$\mathcal{X}=\left\{x_{i}\right\}_{i=1}^{N_{u}}$,还有一个辅助数据集$\mathcal{Z}=\left\{z_{i}, w_{i}\right\}_{i=1}^{N_{a}}$,这里的$z_{i}$代表每一个人物图片,$w_{i}$是对应的标签,$N_{a}$是辅助数据集的大小。注意这里的目标域数据集和辅助数据集的人物是完全不重叠的。
2.软多标签
软多标签其实就是学习一个映射函数$l(\cdot)$,对于所有的参考人物有$y=l(x, \mathcal{Z}) \in(0,1)^{N_{p}}$,所有维度的总和加起来等于1.同时在软多标签的指导下,我们还希望学习到一个有区分力的嵌入$f(\cdot)$,同时要求$\|f(\cdot)\|_{2}=1$。作者还引入了一个参考代理的概念即$\left\{a_{i}\right\}_{i=1}^{N_{p}}$。(这个会放到后面说,暂时可以就认为它是辅助数据集中一个参考人(这个人有多张图片)的特征表达),同时有$\|a_i\|_{2}=1$.(不得不吐槽,作者对于公式的定义真是一团糟,下标不一致,解释也不清晰,比如$l(\cdot)$里面一会的参数是样本,一会又是特征,上标一会是$N_{a}$,一会又成了$N_{p}$,其实$N_{a}$是图片张数,$N_{p}$是行人个数)。
因为对于软多标签y来说,它的所有维度之和为1,所以可以使用如下定义:
$y^{(k)}=l\left(f(x),\left\{a_{i}\right\}_{i=1}^{N_{p}}\right)^{(k)}=\frac{\exp \left(a_{k}^{\mathrm{T}} f(x)\right)}{\sum_{i} \exp \left(a_{i}^{\mathrm{T}} f(x)\right)}$
这里的$a_i$就是参考代理了。
3.困难负样本挖掘
困难负样本挖掘对于学习到有区分力的特征是很有效的。在无标注的目标域上面因为缺少ID所以困难负样本的判断成了一个问题。作者做了一个这样的假设:如果一对样本$x_i,x_j$拥有很高的特征相似度$f(x_i)^{T}f(x_j)$,那么我们就认为这是一对相似样本,如果相似样本的其他特性也相似,那么它很可能是一个正样本,反之就是一个负样本。这里就把软多标签当作是其他特性。接着提出如下的相似度定义,使用的是逐元素的交运算,最后可以简化成使用L1距离进行表示。
$A\left(y_{i}, y_{j}\right)=y_{i} \wedge y_{j}=\Sigma_{k} \min \left(y_{i}^{(k)}, y_{j}^{(k)}\right)=1-\frac{\left\|y_{i}-y_{j}\right\|_{1}}{2}$
其实这里的物理意义相当于每个代理人在进行投票,对这一对图像是否属于同一个人进行表决。作者做了如下的公式化:
$\begin{aligned} \mathcal{P} &=\left\{(i, j) | f\left(x_{i}\right)^{\mathrm{T}} f\left(x_{j}\right) \geq S, A\left(y_{i}, y_{j}\right) \geq T\right\} \\ \mathcal{N} &=\left\{(k, l) | f\left(x_{k}\right)^{\mathrm{T}} f\left(x_{l}\right) \geq S, A\left(y_{k}, y_{l}\right)<T\right\} \end{aligned}$
上式中的$p$是一个代表比例的参数,对于未标注的目标域来说将有$M=N_u*(N_u-1)/2$个图像对,我们认为其中$pM$个是有着最高的特征相似度的,同理有$pM$个是有着最高的软标签相似度的。这里的$S,T$就是$pM$的位置处对应的阈值了。多标签引导的有区分力嵌入学习(MDL)就被定义为:
$L_{M D L}=-\log \frac{\overline{P}}{\overline{P}+\overline{N}}$
其中:
$\begin{aligned} \overline{P} &=\frac{1}{|\mathcal{P}|} \Sigma_{(i, j) \in \mathcal{P}} \exp \left(-\left\|f\left(z_{i}\right)-f\left(z_{j}\right)\right\|_{2}^{2}\right) \\ \overline{N} &=\frac{1}{|\mathcal{N}|} \Sigma_{(k, l) \in \mathcal{N}} \exp \left(-\left\|f\left(z_{k}\right)-f\left(z_{l}\right)\right\|_{2}^{2}\right) \end{aligned}$
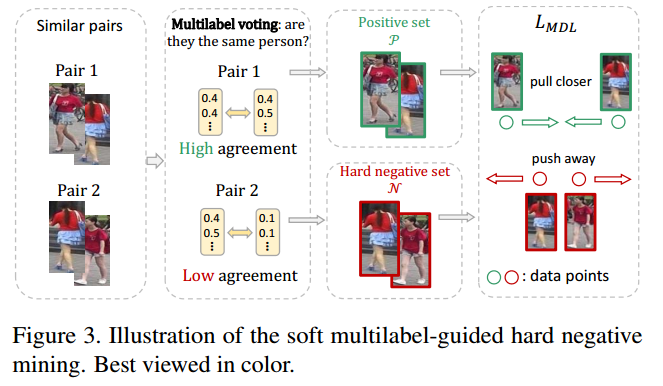
通过最小化$L_{M D L}$来学习有区分力的嵌入(这个公式的物理意义是什么?)。这里的$P,N$在模型训练中是动态的,应该使用每一轮更新后的特征嵌入来构造。因为这个原因,作者将$M$替换成了$M_{batch}=N_{batch}*(N_{batch}-1)/2$,$N_{batch}$指的就是每一小批中无标注图像的个数。(因为样本中正样本对远远多于负样本这样一来每一小批中真的会存在正例吗?)
4.跨视角一致的软多标签学习
因为行人重识别要求识别不同相机视角下的行人,所以在进行跨视角匹配时,软多标签需要保持良好的一致性。从数据分布的视角来看,比较特性的分布应该只取决于目标域人物外观的分布而与相机视角无关。举个例子来说,如果目标域是一个寒冷的开放市场,顾客往往都是穿着深色衣服,那么软标签中有着高相似度的元素对应的参考人物也应该是穿着深色衣服,而不管是哪个目标相机视角拍摄的。换句话来说,就是每个相机视角下的软多标签分布应该与目标域的分布一致。通过以上分析,作者引入了跨视角一致的软多标签学习损失:
$L_{C M L}=\Sigma_{v} d\left(\mathbb{P}_{v}(y), \mathbb{P}(y)\right)^{2}$
$\mathbb{P}_(y)$是数据集$X$的软标签分布,$\mathbb{P}_{v}(y)$是$X$中第$v$个相机视角的软标签分布,$d(\cdot,\cdot)$是两个分布之间的距离。因为作者通过经验观察发现软多标签大致符合一个$log-normal$分布,所以使用简化的$2-Wasserstein$距离作为度量标准。
$L_{C M L}=\Sigma_{v}\left\|\mu_{v}-\mu\right\|_{2}^{2}+\left\|\sigma_{v}-\sigma\right\|_{2}^{2}$
$\mu/\sigma$分别代表log软多标签的均值与方差向量,$\mu_v/\sigma_v$就代表第v个相机视角下log软多标签的均值与方差向量。
5.参考代理学习
参考代理是在特征嵌入中表示一个唯一的参考人,起到紧凑的特征摘要器的概念。因此,参考代理之间应该相互区分同时每一个参考代理都应该能够代表所有对应的行人图像。(作者原文表达佶屈聱牙,真让人怀疑这不是CVPR定稿)
$L_{A L}=\Sigma_{k}-\log l\left(f\left(z_{k}\right),\left\{a_{i}\right\}\right)^{\left(w_{k}\right)}=\Sigma_{k}-\log \frac{\exp \left(a_{w_{k}}^{\mathrm{T}} f\left(z_{k}\right)\right)}{\Sigma_{j} \exp \left(a_{j}^{\mathrm{T}} f\left(z_{k}\right)\right)}$
$z_k$是辅助数据集的第$k$个行人图像,它的标签为$w_k$.对于这个公式我的理解是通过最小化$L_{A L}$,我们能够为每个参考人学习到一个混合的特征表达,$a_{w_k}$表示的就是标签为$w_k$的这个行人的特征表达,$L_{A L}$中后一项的交叉熵强调了每个行人表达的区分力。参考代理学习的另一个的隐含重要作用是增强了软多标签函数$l(\cdot)$的有效性,对于辅助数据集的图片$z_k$,我们计算的$L_{A L}这个式子的后一项与软标签$\hat{y}_{k}=l\left(f\left(z_{k}\right),\left\{a_{i}\right\}_{i=1}^{N_{p}}\right)$完全相同,,$L_{A L}$的目的是希望软标签能够与真实的标签$\hat{w}_{k}=[0, \cdots, 0,1,0, \cdots, 0]$足够接近。当$z_i,z_j$属于同一个人时$A\left(\hat{w}_{i}, \hat{w}_{j}\right)=1$,否则为0.(相当于这一块属于有监督学习,能够保证学习到的$l(\cdot)$函数是有效的).但是$L_{A L}$其实只在辅助数据集做最小化,为了提高软多标签函数在目标数据集上的有效性,接着提出学习如下的联合嵌入。
要使得软多标签函数在目标域上还能用,就得解决域偏移。作者提出使用挖掘跨域的困难负样本(也就是包含无标注人物$f(x)$和额外参考人$a_i$的一对,因为他们肯定不是一对正例)来修正跨域分布不对齐。做法就是针对每个$a_i$,找出与它接近的无标注人物f(x),他们之间不管外观多相近,都需要有很强的特征区分度。
$L_{R J}=\Sigma_{i} \Sigma_{j \in \mathcal{M}_{i}} \Sigma_{k : w_{k}=i}\left[m-\left\|a_{i}-f\left(x_{j}\right)\right\|_{2}^{2}\right]_{+}+\left\|a_{i}-f\left(z_{k}\right)\right\|_{2}^{2}$
$\mathcal{M}_{i}=\left\{j\left\|a_{i}-f\left(x_{j}\right)\right\|_{2}^{2}<m\right\}$也就是代表数据与参考$a_i$的距离,$m=1$在理论上是合理的,$[\cdot]_+$是一个hinge函数,后面的center-pulling项$\left\|a_{i}-f\left(z_{k}\right)\right\|_{2}^{2}$增强了参考代理的表达性,因为$z_k$其实是辅助数据集标签为$w_k$的样本。总的来说$L_{R J}$的作用是利用辅助数据集和目标域的不重合来进行adaptation,同时要求辅助域中参考代理向量不能因为前一项而跑偏,继续保持良好的代表能力。
这里的$\mathcal{M}_{i}=\left\{j\left\|a_{i}-f\left(x_{j}\right)\right\|_{2}^{2}<m\right\}$。最终的参考代理学习为:
$L_{R A L}=L_{A L}+\beta L_{R J}$
6.模型训练与测试
本文提出的整体的损失函数如下:
$L_{M A R}=L_{M D L}+\lambda_{1} L_{C M L}+\lambda_{2} L_{R A L}$
在测试时计算查询与图库图片的特征余弦相似度,然后按照距离排序获得检索结果。

$L_{A L}


