《机器学习》上机实践（1）

《机器学习》上机实践（1）

代码有参考往年学长的博客orz：转这里麻了麻了，很认真的看了好久才懂咋实现的

题目

• Iris数据集已与常见的机器学习工具集成，请查阅资料找出MATLAB平台或Python平台加载内置Iris数据集方法，并简要描述该数据集结构。

核心代码如下：

from sklearn import datasets
import pandas as pd
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.stats import multivariate_normal as gaussian_cal
Iris = datasets.load_iris()

数据结构如下：

很明显是一个字典

{

​ data:...

​ target:...

​ target_names:...

​ ...

}

比较主要的就这三个关键字，data是每个数据的特征数组，target是每个数据的归类，target_names是每类数据的名字

• Iris数据集中有一个种类与另外两个类是线性可分的，其余两个类是线性不可分的。请你通过数据可视化的方法找出该线性可分类并给出判断依据。

​ orzPCA降维可以降一维画四张图挺不错的，但是我还是老实研究了一波三维图

​ 很明显setosa和另外两个是线性可分的，剩下两类是线性不可分的

核心代码

from sklearn import datasets
import pandas as pd
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.stats import multivariate_normal as gaussian_cal
def show_3D(data,iris_type):
    xx = [[0, 1, 2], [1, 2, 3], [0, 2, 3], [0, 1, 3]]
    fig = plt.figure(figsize=(20, 20))
    feature = ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
    for i in range(4):
        ax = fig.add_subplot(221 + i, projection="3d")
        ax.scatter(data[iris_type == 0, xx[i][0]], data[iris_type == 0, xx[i][1]], data[iris_type == 0, xx[i][2]],
                   c='r', marker='o', label='setosa')
        ax.scatter(data[iris_type == 1, xx[i][0]], data[iris_type == 1, xx[i][1]], data[iris_type == 1, xx[i][2]],
                   c='g', marker='x',
                   label='vesicolor')
        ax.scatter(data[iris_type == 2, xx[i][0]], data[iris_type == 2, xx[i][1]], data[iris_type == 2, xx[i][2]],
                   c='b', marker='^',
                   label='virginica')
        ax.set_zlabel(feature[xx[i][2]])
        ax.set_xlabel(feature[xx[i][0]])
        ax.set_ylabel(feature[xx[i][1]])
        plt.legend(loc=0)
    plt.show()

• 去除Iris数据集中线性不可分的类中最后一个，余下的两个线性可分的类构成的数据集命令为Iris_linear，请使用留出法将Iris_linear数据集按7:3分为训练集与测试集，并使用训练集训练一个MED分类器，在测试集上测试训练好的分类器的性能，给出《模式识别与机器学习-评估方法与性能指标》中所有量化指标并可视化分类结果。

留出法这边采用的是等比例每类里随机取数

def hold_out_partition(data_linear,iris_type_linear):
    import random

    train_data = []
    train_type = []
    test_data = []
    test_type = []
    first_cur = []
    second_cur = []
    for i in range(len(data_linear)):
        if iris_type_linear[i] == 0:
            first_cur.append(i)
        else:
            second_cur.append(i)
    k = len(first_cur)-1
    #七三开训练集和测试集
    train_size = int(len(first_cur) * 7 / 10)
    test_size = int(len(first_cur) * 3 / 10)
    for i in range(0,train_size):
        cur = random.randint(0,k)
        train_data.append(data_linear[first_cur[cur]])
        train_type.append(iris_type_linear[first_cur[cur]])
        k = k - 1
        first_cur.remove(first_cur[cur])
    for i in range(len(first_cur)):
        test_data.append(data_linear[first_cur[i]])
        test_type.append(iris_type_linear[first_cur[i]])

    k = len(second_cur)-1
    train_size = int(len(second_cur) * 7 / 10)
    test_size = int(len(second_cur) * 3 / 10)
    for i in range(0, train_size):
        cur = random.randint(0, k)
        train_data.append(data_linear[second_cur[cur]])
        train_type.append(iris_type_linear[second_cur[cur]])
        k = k - 1
        second_cur.remove(second_cur[cur])
    for i in range(len(second_cur)):
        test_data.append(data_linear[second_cur[i]])
        test_type.append(iris_type_linear[second_cur[i]])

    return np.asarray(train_data,dtype="float64"),np.asarray(train_type,dtype="int16"),np.asarray(test_data,dtype="float64"),np.asarray(test_type,dtype="int16")

由于是线性可分的，各项指标到达1.0

Recall= 1.000000

Specify= 1.000000

Precision= 1.000000

F1 Score= 1.000000

这边界平面真是给画去世了……得到均值两点后就有法向量和平面上一点，平面方程就有了

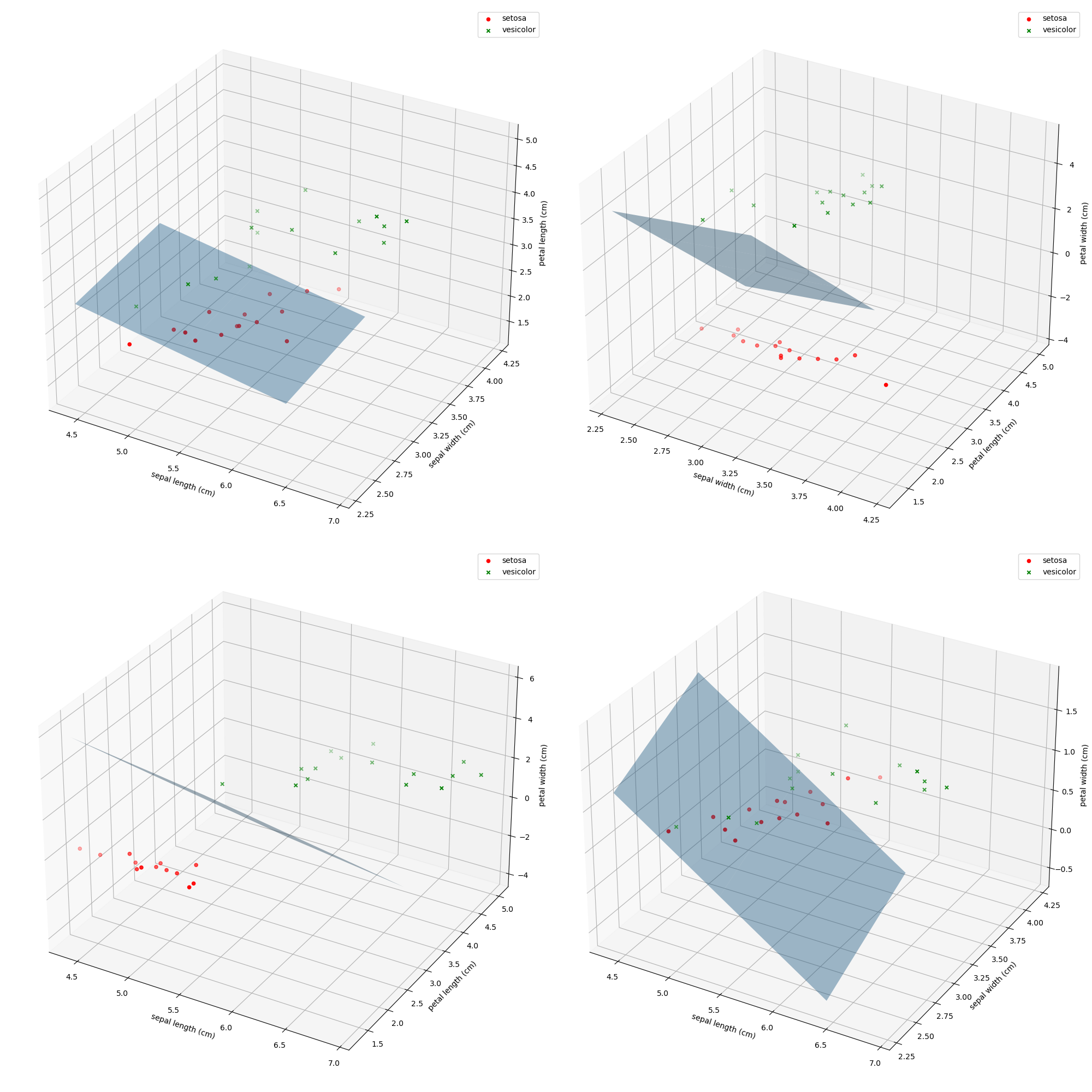
from sklearn import datasets
import pandas as pd
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.stats import multivariate_normal as gaussian_cal
def MED_linear_classification(data,iris_type,t,f,flag):
    data_linear,iris_type_linear=getIrisLinear(data,iris_type,flag)
    train_data,train_type,test_data,test_type = hold_out_partition(data_linear,iris_type_linear)
    c1 = []
    c2 = []
    n1=0
    n2=0
    #计算均值
    for i in range(len(train_data)):
        if train_type[i] == 1:
            n1+=1
            c1.append(train_data[i])
        else:
            n2+=1
            c2.append(train_data[i])
    c1 = np.asarray(c1)
    c2 = np.asarray(c2)
    z1 = c1.sum(axis=0)/n1
    z2 = c2.sum(axis=0)/n2
    test_result = []
    for i in range(len(test_data)):
        result = np.dot(z2-z1,test_data[i]-(z1+z2)/2)
        test_result.append(np.sign(result))
    test_result = np.array(test_result)
    TP = 0
    FN = 0
    TN = 0
    FP = 0
    for i in range(len(test_result)):
        if(test_result[i]>=0 and test_type[i]==t):
            TP+=1
        elif(test_result[i]>=0 and test_type[i]==f):
            FN+=1
        elif(test_result[i]<0 and test_type[i]==t):
            FP+=1
        elif(test_result[i]<0 and test_type[i]==f):
            TN+=1
    Recall = TP/(TP+FN)
    Precision = TP/(TP+FP)
    print("Recall= %f"% Recall)
    print("Specify= %f"% (TN/(TN+FP)))
    print("Precision= %f"% Precision)
    print("F1 Score= %f"% (2*Recall*Precision/(Recall+Precision)))
    #开始画图
    xx = [[0, 1, 2], [1, 2, 3], [0, 2, 3], [0, 1, 3]]
    iris_name =['setosa','vesicolor','virginica']
    iris_color = ['r','g','b']
    iris_icon = ['o','x','^']
    fig = plt.figure(figsize=(20, 20))
    feature = ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
    for i in range(4):
        ax = fig.add_subplot(221 + i, projection="3d")
        X = np.arange(test_data.min(axis=0)[xx[i][0]],test_data.max(axis=0)[xx[i][0]],1)
        Y = np.arange(test_data.min(axis=0)[xx[i][1]],test_data.max(axis=0)[xx[i][1]],1)
        X,Y = np.meshgrid(X,Y)
        m1 = [z1[xx[i][0]],z1[xx[i][1]],z1[xx[i][2]]]
        m2 = [z2[xx[i][0]], z2[xx[i][1]], z2[xx[i][2]]]
        m1 = np.array(m1)
        m2 = np.array(m2)
        m = m2-m1
        #公式化简可得
        Z = (np.dot(m,(m1+m2)/2)-m[0]*X-m[1]*Y)/m[2]
        ax.scatter(test_data[test_result >= 0, xx[i][0]], test_data[test_result>=0, xx[i][1]], test_data[test_result >= 0, xx[i][2]],
                   c=iris_color[t], marker=iris_icon[t], label=iris_name[t])
        ax.scatter(test_data[test_result < 0, xx[i][0]], test_data[test_result < 0, xx[i][1]],
                   test_data[test_result < 0, xx[i][2]],
                   c=iris_color[f], marker=iris_icon[f], label=iris_name[f])
        ax.set_zlabel(feature[xx[i][2]])
        ax.set_xlabel(feature[xx[i][0]])
        ax.set_ylabel(feature[xx[i][1]])
        ax.plot_surface(X,Y,Z,alpha=0.4)
        plt.legend(loc=0)
    plt.show()

• 将Iris数据集白化，可视化白化结果并于原始可视化结果比较，讨论白化的作用。

只能说numpy真的很香，能支持向量运算，白化后数据确实直观很多

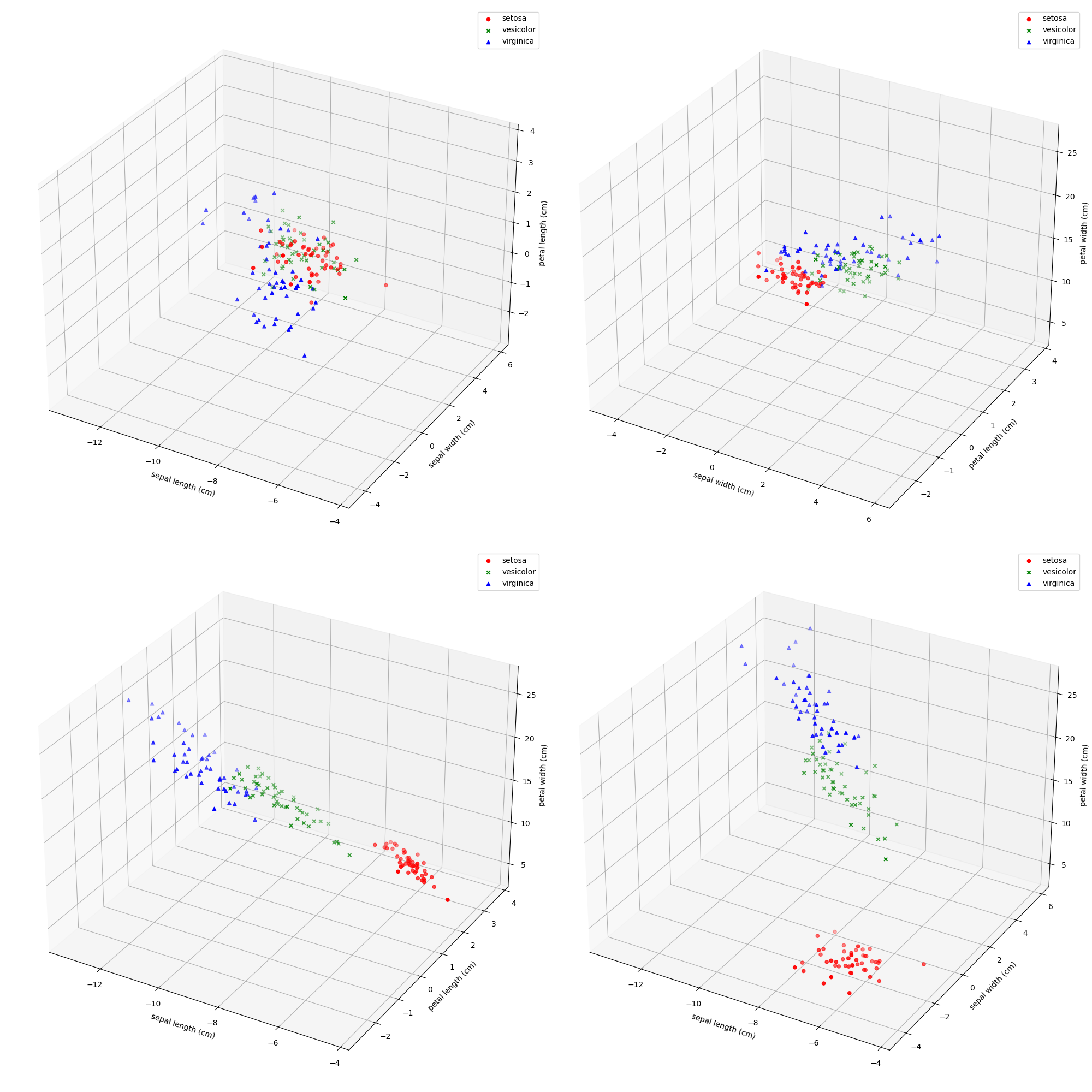
代码如下：

def whiten_feature(data):
    Ex = np.cov(data,rowvar=False)#这个一定要加……因为我们计算的是特征的协方差
    a,w1 = np.linalg.eig(Ex)
    w1 = np.real(w1)
    module = []
    for i in range(w1.shape[1]):
        sum = 0
        for j in range(w1.shape[0]):
            sum += w1[i][j]**2
        module.append(sum**0.5)
    module = np.asarray(module,dtype="float64")
    w1 = w1/module
    a = np.real(a)
    a=a**(-0.5)
    w2 = np.diag(a)
    w = np.dot(w2,w1.transpose())
    for i in range(w.shape[0]):
        for j in range(w.shape[1]):
            if np.isnan(w[i][j]):
                w[i][j]=0
    #print(w)
    return np.dot(data,w)

• 去除Iris数据集中线性可分的类，余下的两个线性不可分的类构成的数据集命令为Iris_nonlinear，请使用留出法将Iris_nonlinear数据集按7:3分为训练集与测试集，并使用训练集训练一个MED分类器，在测试集上测试训练好的分类器的性能，给出《模式识别与机器学习-评估方法与性能指标》中所有量化指标并可视化分类结果。讨论本题结果与3题结果的差异。

同样的代码不一样的数据集，由于随机性以及数据的线性不可分的原因，各项指标每次测量都不一样，有的时候会有除0风险orz，对边界的确定影响很大

Recall= 0.066667

Specify= 0.066667

Precision= 0.066667

F1 Score= 0.066667

• 请使用5折交叉验证为Iris数据集训练一个多分类的贝叶斯分类器。给出平均Accuracy，并可视化实验结果。与第3题和第5题结果做比较，讨论贝叶斯分类器的优劣。

只能说，做麻了，效果确实比MED好

Accuracy = 0.9733333333333334，基本在这个值上下浮动，因为k折验证也是随机取点

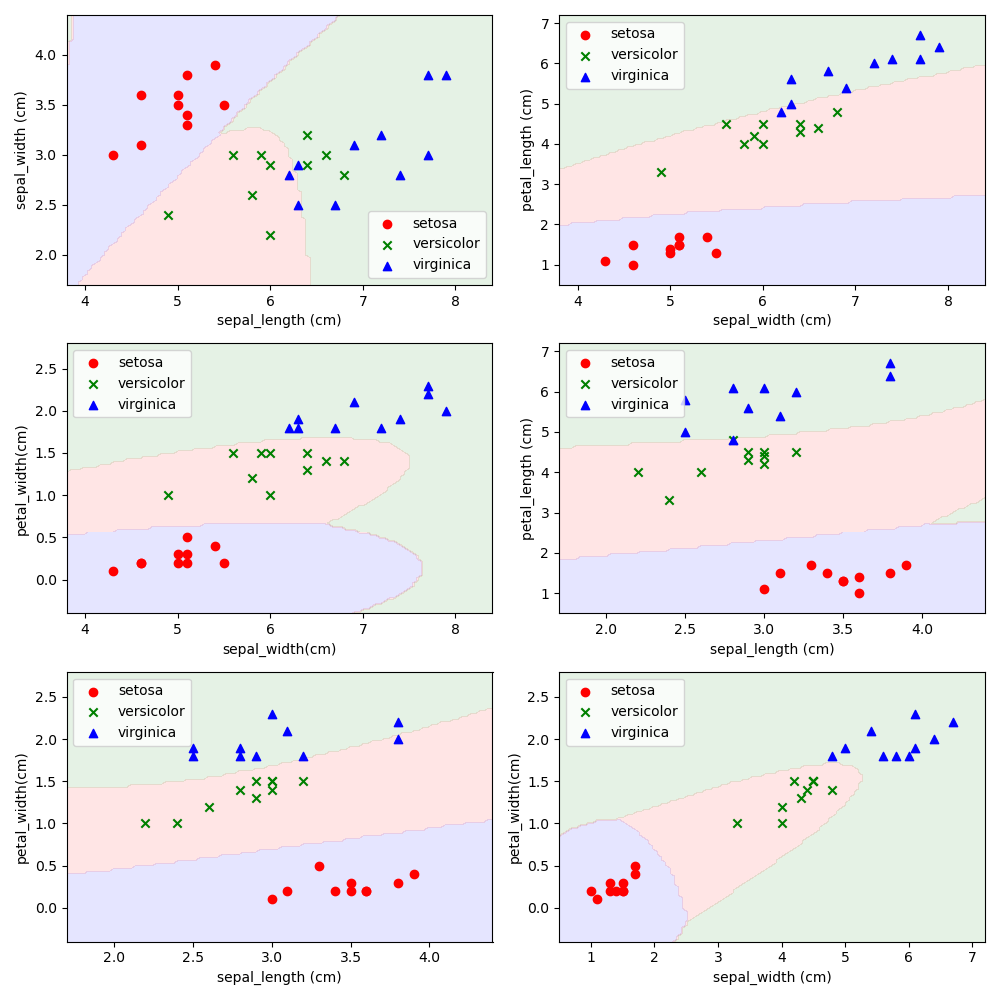
代码：

from sklearn import datasets
import pandas as pd
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.stats import multivariate_normal as gaussian_cal
def k_split(data,iris_type,num):
    import random
    testSet = []
    testType = []
    first_cur = []
    second_cur = []
    third_cur = []
    for i in range(len(iris_type)):
        if iris_type[i] == 0:
            first_cur.append(i)
        elif iris_type[i] == 1:
            second_cur.append(i)
        else:
            third_cur.append(i)
    match_size = int(len(first_cur)/num)
    size = len(first_cur)-1
    train_data = []
    train_type = []
    for i in range(num):
        k = match_size
        train_data = []
        train_type = []
        for j in range(match_size):
            cur = random.randint(0, size)
            train_data.append(data[first_cur[cur]])
            train_type.append(iris_type[first_cur[cur]])
            first_cur.remove(first_cur[cur])

            cur = random.randint(0, size)
            train_data.append(data[second_cur[cur]])
            train_type.append(iris_type[second_cur[cur]])
            second_cur.remove(second_cur[cur])

            cur = random.randint(0, size)
            train_data.append(data[third_cur[cur]])
            train_type.append(iris_type[third_cur[cur]])
            third_cur.remove(third_cur[cur])
            size = size-1
        testSet.append(train_data)
        testType.append(train_type)
    return np.asarray(testSet),np.asarray(testType)

class Bayes_Parameter():
    def __init__(self,mean,cov,type):
        self.mean = mean
        self.cov = cov
        self.type = type

class Bayes_Classifier():
    #必须存入k-1个训练集的每个高斯分布
    def __init__(self):
        self.parameters=[]
    def train(self,data,iris_type):
        for type in set(iris_type):
            selected = iris_type==type
            select_data = data[selected]
            mean = np.mean(select_data,axis=0)
            cov = np.cov(select_data.transpose())
            self.parameters.append(Bayes_Parameter(mean,cov,type))
    def predict(self,data):
        result = -1
        probability = 0
        for parameter in self.parameters:
            temp = gaussian_cal.pdf(data,parameter.mean,parameter.cov)
            if temp > probability:
                probability = temp
                result = parameter.type
        return result

def Bayes_Classification_K_split(data,iris_type,num):
    train_dataset,train_typeset = k_split(data,iris_type,num)
    accuracy = 0
    best_result = []
    best_train_data = []
    best_train_type = []
    best_test_data = []
    best_test_type = []
    max_accuracy = 0
    for i in range(num):
        data_num = 0
        type_num = 0
        train_data = []
        train_type = []
        for j in range(num):
            if i != j:
                if data_num*type_num == 0:
                    train_data = train_dataset[j]
                    train_type = train_typeset[j]
                    data_num+=1
                    type_num+=1
                else:
                    train_data = np.concatenate((train_data,train_dataset[j]),axis=0)
                    train_type = np.concatenate((train_type,train_typeset[j]),axis=0)
            Bayes_classifier = Bayes_Classifier()
            Bayes_classifier.train(train_data,train_type)
        predict_result = [Bayes_classifier.predict(x) for x in train_dataset[i]]
        right = 0
        all = 0
        for j in range(len(predict_result)):
            if predict_result[j] == train_typeset[i][j]:
                right+=1
            all+=1
        tempaccuracy = right/all
        if tempaccuracy > max_accuracy:
            max_accuracy = tempaccuracy
            best_train_data = train_data
            best_train_type = train_type
            best_test_data = train_dataset[i]
            best_test_type = train_typeset[i]
            best_result = np.asarray(predict_result,dtype="int")
        accuracy+=tempaccuracy
    show_2D(best_train_data,best_train_type,best_test_data,best_test_type,best_result)
    return accuracy/5

def show_2D(train_data,train_type,test_data,test_type,result):
    import math
    fig = plt.figure(figsize=(10,10))
    xx = [[0,1],[0,2],[0,3],[1,2],[1,3],[2,3]]
    yy = [["sepal_length (cm)", "sepal_width (cm)"],
          ["sepal_width (cm)", "petal_length (cm)"],
          ["sepal_width(cm)", "petal_width(cm)"],
          ["sepal_length (cm)", "petal_length (cm)"],
          ["sepal_length (cm)", "petal_width(cm)"],
          ["sepal_width (cm)", "petal_width(cm)"]]
    for i in range(6):
        ax = fig.add_subplot(321+i)
        x_max,x_min = test_data.max(axis=0)[xx[i][0]]+0.5,test_data.min(axis=0)[xx[i][0]]-0.5
        y_max,y_min = test_data.max(axis=0)[xx[i][1]]+0.5,test_data.min(axis=0)[xx[i][1]]-0.5
        xlist = np.linspace(x_min, x_max, 100)
        ylist = np.linspace(y_min, y_max, 100)
        X, Y = np.meshgrid(xlist,ylist)
        bc = Bayes_Classifier()
        bc.train(train_data[:,xx[i]],train_type)
        xy = [np.array([xx,yy]).reshape(1,-1 ) for xx,yy in zip(np.ravel(X),np.ravel(Y))]
        zz = np.array([bc.predict(x) for x in xy])
        Z = zz.reshape(X.shape)
        plt.contourf(X,Y,Z,2,alpha=.1,colors=('blue','red','green'))
        ax.scatter(test_data[result==0,xx[i][0]],test_data[result==0,xx[i][1]],c='r',marker='o',label='setosa')
        ax.scatter(test_data[result == 1, xx[i][0]], test_data[result == 1, xx[i][1]], c='g', marker='x',
                   label='versicolor')
        ax.scatter(test_data[result == 2, xx[i][0]], test_data[result == 2, xx[i][1]], c='b', marker='^', label='virginica')
        ax.set_xlabel(yy[i][0])
        ax.set_ylabel(yy[i][1])
        ax.legend(loc=0)
    plt.show()

感想

其实分类海星，就是作图实在是……代码实现很麻，主要是对numpy，sklearn，scipy，matplotlib这些库不是很熟吧，除了学长的博客也查了很多其他这些库的内容，包括如何用python画三维图，sklearn计算高斯分布概率啥的，对我个人来说锻炼还是很多的吧，很久没写代码了orz