个人项目
| 这个作业属于哪个课程 | 2020春北航计算机学院软件工程(罗杰 任健) |
| 这个作业的要求在哪里 | 个人项目作业 |
| 我在这个课程的目标是 | 增强软件开发能力,增强沟通表达能力 |
| 这个作业在哪个具体方面帮助我实现目标 | 完成个人项目,接触软件开发流程 |
| 教学班级 | 006 |
| github地址 | https://github.com/Therp-GY/IntersectProject |
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 100 | 180 |
| · Design Spec | · 生成设计文档 | 10 | 10 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 5 | 5 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 5 | 5 |
| · Design | · 具体设计 | 80 | 100 |
| · Coding | · 具体编码 | 120 | 300 |
| · Code Review | · 代码复审 | 30 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 40 | 60 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 60 | 100 |
| · Size Measurement | · 计算工作量 | 10 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 20 | 20 |
| 合计 | 490 | 830 |
实际耗时远远大于预估时间。1. 对语言不熟练,导致简单代码也花费了一些时间 2.第一次按照规范流程完成项目,在一个个环节上也不够熟练,问题颇多。
解题思路
直线表示方法:ax + by + c = 0
圆表示方式:(x-a)^2 + (y-b)^2 = r^2
直线与直线之间求交点直接联立方程求解,然而圆与直线、圆与圆方程求解实现并不简单,于是关于圆交点的求解用几何方法,只需要引入向量类(实际上就是交点类),进行向量加减法即可完成求解。
关于精度:我使用double类型,因此需要引入eps精度。
关于重复点:由于时间原因,我使用较为暴力的方法。建立一个交点容器和一个几何对象容器,在每次输入新的几何对象后,求它和几何对象容器中所有几何对象的交点,并将这些交点插入到交点容器中,若容器中已经存在这个交点则不插入。
设计实现过程
my_math.h头文件中定义了三个类,点类、线类、圆类
点类
class Point { double x_; double y_; public: Point(double x, double y); Point(); double get_x()const; double get_y()const; double distance(const Point& point)const; bool operator==(const Point& point) const; bool operator<(const Point& point) const; // 重载用于set容器 Point operator+(const Point& point) const; Point operator-(const Point& point) const; Point operator*(const double& d) const; Point operator/(const double& d) const; friend void operator<<(std::ostream &os, Point &point); }; typedef Point Vector; // 点类就是向量类
线类
class Line { double a; double b; double c; // ax + by + c = 0 public: Line(const Point& p1, const Point& p2); Line(const double& a_, const double& b_, const double& c_); Line(const double& a_, const double& b_, const Point &point); Point find_intersection(const Line &line); // 线和线的交点 double get_a()const; double get_b()const; double get_c()const; Vector get_directionVector()const; // 单位向量 bool operator==(const Line& line); friend void operator<<(std::ostream& os, Line& line); };
圆类
class Circle { Point o; double r; public: Circle(const Point& point, const double r_); Circle(); int find_intersection(const Line& line , Point *p); // 圆和线的交点 int find_intersection(const Circle& circle, Point* p); // 圆和圆的交点 double get_r()const; Point get_o()const; };
关键函数比较离散,并不复杂。线线、圆线都是独立求的,圆圆会转化为圆线相交,逻辑比较简单。
单元测试
对线线测试相交、平行、重合(即报错)情况。通过测试
对线圆测试相交、相切、相离情况。通过测试
对圆圆测试内切、外切、相交、无交点情况。通过测试
并使用GeoGebra进行测试多种几何对象相交情况(未写入单元测试)
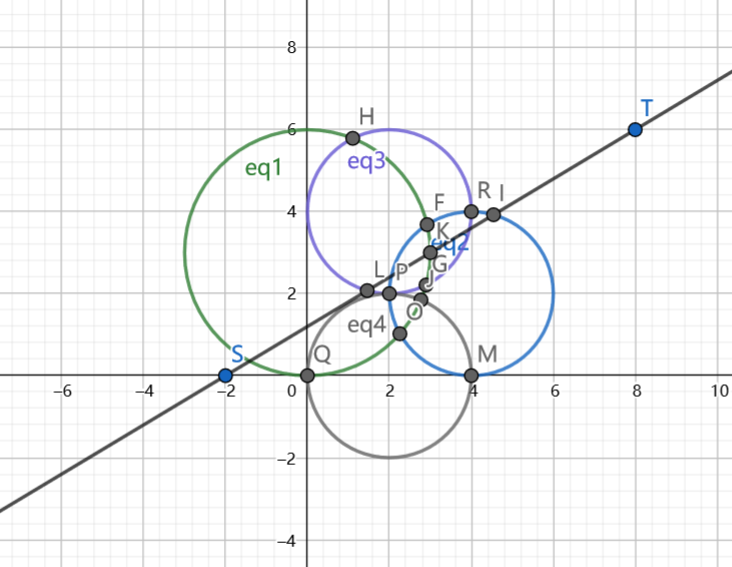
同时每一次版本改变就做回归测试。
性能改进
性能改进上花了约120min,由于对c++一些数据结构并没有清晰的概念,导致在改进上速度很慢。
我最开始选择存储点的容器未map,但是一开始对insert函数的误操作,在insert上又加find函数,导致在查找点时连续进行两次查找,耗时巨大。
在将find去除后,性能探查器得到如下结果。测试数据为5000组。
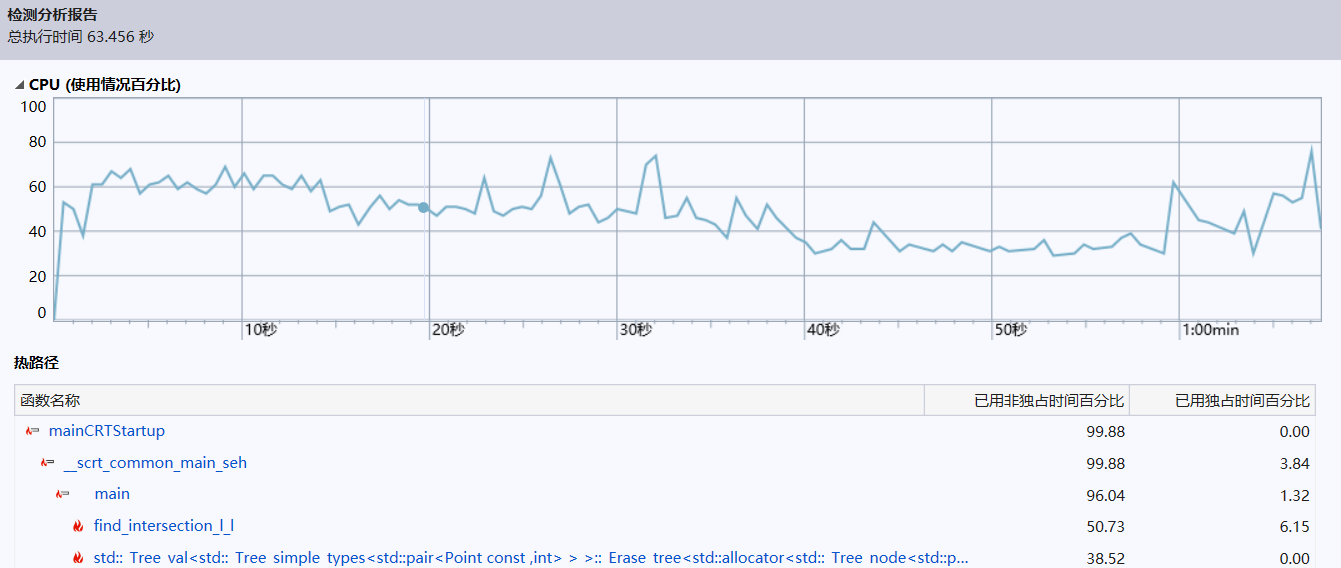
性能消耗最大的函数即find_intersection,因为要遍历所有已有点并完成插入工作。
void find_intersection_l_l(Line &l,vector<Line> &l_list, set<Point>&p_set) { for (unsigned int i = 0; i < l_list.size(); i++) { Point p; Point nopoint(INFINITY, INFINITY); p = l_list[i].find_intersection(l); if (p == nopoint)continue; p_set.insert(p); } }
map效果十分不理想,由此我又使用set存储点,只存储唯一键值。
以下是用set进行5000组测试。
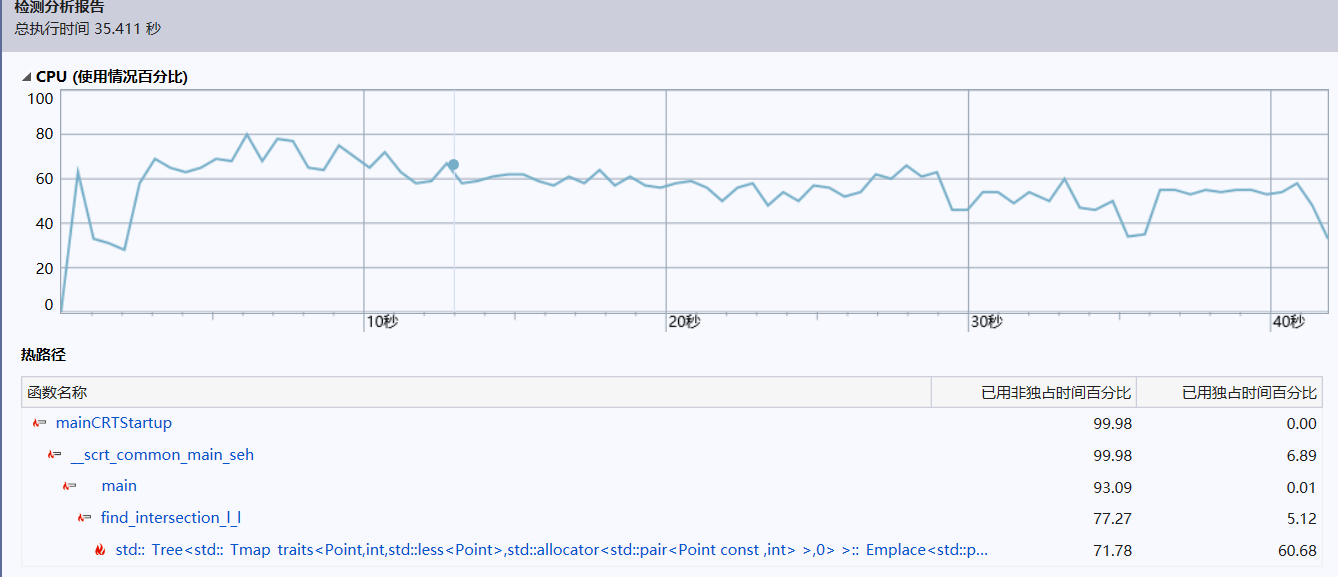
可以看出速度变快了许多,性能有很大改进。
但由于都是有序容器,因此我想尝试无序容器。因此我采用过unordered_set,因为无序查找速度更快。 但并没有很大的效果改进,甚至时间更长了,或许是我的hash函数并没有很好的分配索引,hash查找比起有序查找在性能上没有显著进步。
代码说明
线线求交点,直接联立直线方程求解。
Point Line::find_intersection(const Line& line) { if (*this == line) { std::cout << "两条线重合, 无数个交点" << std::endl; /*abort();*/ } else { if (b * line.a - a * line.b == 0) { return Point(); } else { double x; double y; y = (a * line.c - c * line.a) / (b * line.a - a * line.b); if (a != 0) { x = (- c - b * y) / a; } else { x = (-line.c - line.b * y) / line.a; } return Point(x, y); } } }
圆线求交点,算出圆心到直线的距离,再用勾股定理算出弦长并转化为向量,然后求解点。
int Circle::find_intersection(const Line& line, Point* p) { int n; // 交点个数 Vector line_vector = line.get_directionVector(); // line 的单位向量 Line line_h(-line.get_b(), line.get_a(), o); // 和 line 垂直且过圆心的垂线 line_h Point i1 = line_h.find_intersection(line); // l_h 和 line 的交点 i1 double d = i1.distance(o); // i1 到 圆心 o 的 距离 double l = sqrt(pow(r, 2) - pow(d, 2)); // sqrt(r^2 - d^2) Vector v = line_vector* l; *p = i1 + line_vector * l; *(p+1) = i1 - line_vector * l; if (d > r) { n = 0; return n; } else if (abs(d - r) <= eps) n = 1; else n = 2; return n; }
圆圆求交点,用几何做法比较麻烦,要分别判断是不相交、外切、内切、相交,然后依靠向量求解。
int Circle::find_intersection(const Circle& circle, Point* p) { if (o == circle.o && (r - circle.r) < eps) { std::cout << "两圆重合,无数个交点" << std::endl; /*abort();*/ return 0; } // 交点个数 int n; // 分大小圆 Circle big; Circle small; if (r >= circle.r) { big = *this; small = circle; } else { big = circle; small = *this; } // 判断交点个数 double d = big.o.distance(small.o); if (d > (big.r + small.r) || d < big.r - small.r) { n = 0; return n; } else if (abs(d - (big.r + small.r)) <= eps) { // 小圆外切 n = 1; Vector v1 = small.o - big.o; // 大圆圆心射向小圆圆心的向量 v1 = v1 * (big.r / (big.r + small.r)); *p = big.o + v1; return n; } else if (abs(d - (big.r - small.r)) <= eps) { // 小圆内切 n = 1; Vector v1 = small.o - big.o; // 大圆圆心射向小圆圆心的向量 v1 = v1 / big.o.distance(small.o) * big.r; *p = big.o + v1; return n; } else { // 2个交点 d ,r1,r2形成三角形 n = 2; Vector v1 = small.o - big.o; v1 = v1 / big.o.distance(small.o); // 单位向量 double x = (pow(big.r, 2) - pow(small.r, 2) + pow(d, 2)) / (2 * d); v1 = v1 * x; Point cross = big.o + v1; Line l(v1.get_x(), v1.get_y(), cross); big.find_intersection(l, p); return n; } return 0; }
是否有运行警告
无





