差分(Difference)
“前缀和”和“差分”是一对互逆运算,“差分”可以维护多次对序列的一个区间修改一个数。
一维差分(One-dimensional)
描述(Description)
C++ 标准库中实现了差分函数
std::adjacent_difference,定义于头文件<numeric>中
示例(Example)
原数列:\(\left[ 2,\ 3,\ 5,\ 7,\ 11,\ 13,\ 17,\ 19 \right]\)
差分处理之后:\(\left[ 2,\ 1,\ 2,\ 2,\ 4,\ 2,\ 4,\ 2 \right]\)
差分后的数列用前缀和处理后可以得到:\(\left[ 2,\ 3,\ 5,\ 7,\ 11,\ 13,\ 17,\ 19 \right]\)
即为原数列
代码(Code)
- 构建差分数组
void calc(int a[], int b[], int n) { for (int i = 1; i <= n; i ++ ) b[i] = a[i] - a[i -1]; }
- 原数组所有的元素都将加上 \(c\) :
void insert(int b[], int c) { b[1] += c; } - 将区间 \([l,r]\) 内的所有元素加上 \(c\) :
void insert(int b[], int l, int r, int c){ // l 在 r 的左边(或重合) b[l] += c; b[r + 1] -= c; // r + 1 位置开始 +c 和 -c 相互抵消 }
二维差分(Two-dimensional)
示例(Example)
- 原数组 \(a\) 中被选中的子矩阵为 以 \((x_1,y_1)\) 为左上角,以 \((x_2,y_2)\) 为右下角所围成的矩形区域
- \(a\) 数组是 \(b\) 数组的前缀和数组\(b\),对 数组的 \(b[i][j]\) 的修改,会影响到 \(a\) 数组中从 \(a[i][j]\) 后的每一个数。
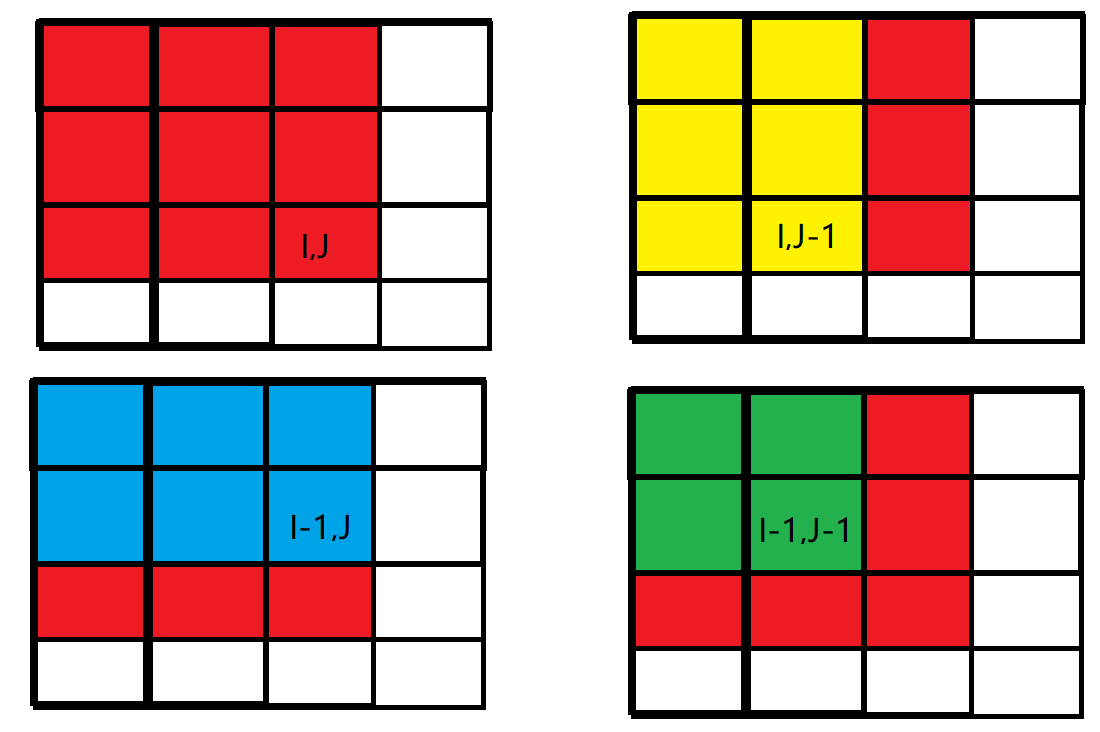
\(b[x_1][y_1] =\ b[x_1][y_1] + c\):蓝色矩形面积的元素都加上 \(c\)
\(b[x_1][y_2 + 1] = b[x_1][y_2 + 1] - c\):绿色矩形面积的元素再减去 \(c\),使其内元素不发生改变
\(b[x_2 + 1][y_1] = b[x_2 + 1][y_1] -c\):紫色矩形面积的元素再减去 \(c\) ,使其内元素不发生改变
\(b[x_2 + 1][y_2 + 1] = b[x_2 + 1][y_2 + 1] +c\):红色矩形面积的元素再加上 \(c\) ,红色部分被减了两次,加上一次 \(c\) ,保证数据准确性
- 最后得到递推公式为:
\[b[i][j] = b[i][j] + b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
\]
代码(Code)
- 构建差分数组
for (int i = 1; i <= n; i ++ ) for (int j = 1; j <= m; j ++ ) insert(i, j, i, j, a[i][j]);
- 插入函数
// 对 b 数组执行插入操作,等价于对a数组中的(x1, y1)到(x2, y2)之间的元素都加上了 c void insert(int x1, int y1, int x2, int y2, int c) { b[x1][y1] += c; b[x2 + 1][y1] -= c; b[x1][y2 + 1] -= c; b[x2 + 1][y2 + 1] += c; // c被减了两遍,加c保证数据准确性 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号