二分查找(Binary Search)
简介(Introduction)
二分查找也称折半查找( Binary Search),它是一种效率较高的查找方法。
折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
描述(Description)
- 二分查找的前提是目标已近排好序(或满足查找条件的序列)
- 二分查找每次对半查找保证其高效性
- 算法分析(以寻找上界为例):
- \(a[mid]\ =\ v\):已经找到了一个符合条件的值,但是它的左边可能还有合适的值,则向左二分:\(r = mid;\)
- \(a[mid]\ >\ v\):要求的位置一定不在当前位置的后面,但是当前位置可能是答案(数组中没有目标值,并且当前位置是第一个大于目标值的位置),则向左二分:\(r = mid;\)
- \(a[mid]\ <\ v\):要求的位置一定不在当前位置以及当前位置的前面,则向右二分:\(l = mid + 1;\)
时间复杂度:\(O(\log n)\)
示例(Example)
1. 二分查找下界
-
在目标数组中找 \(2\):
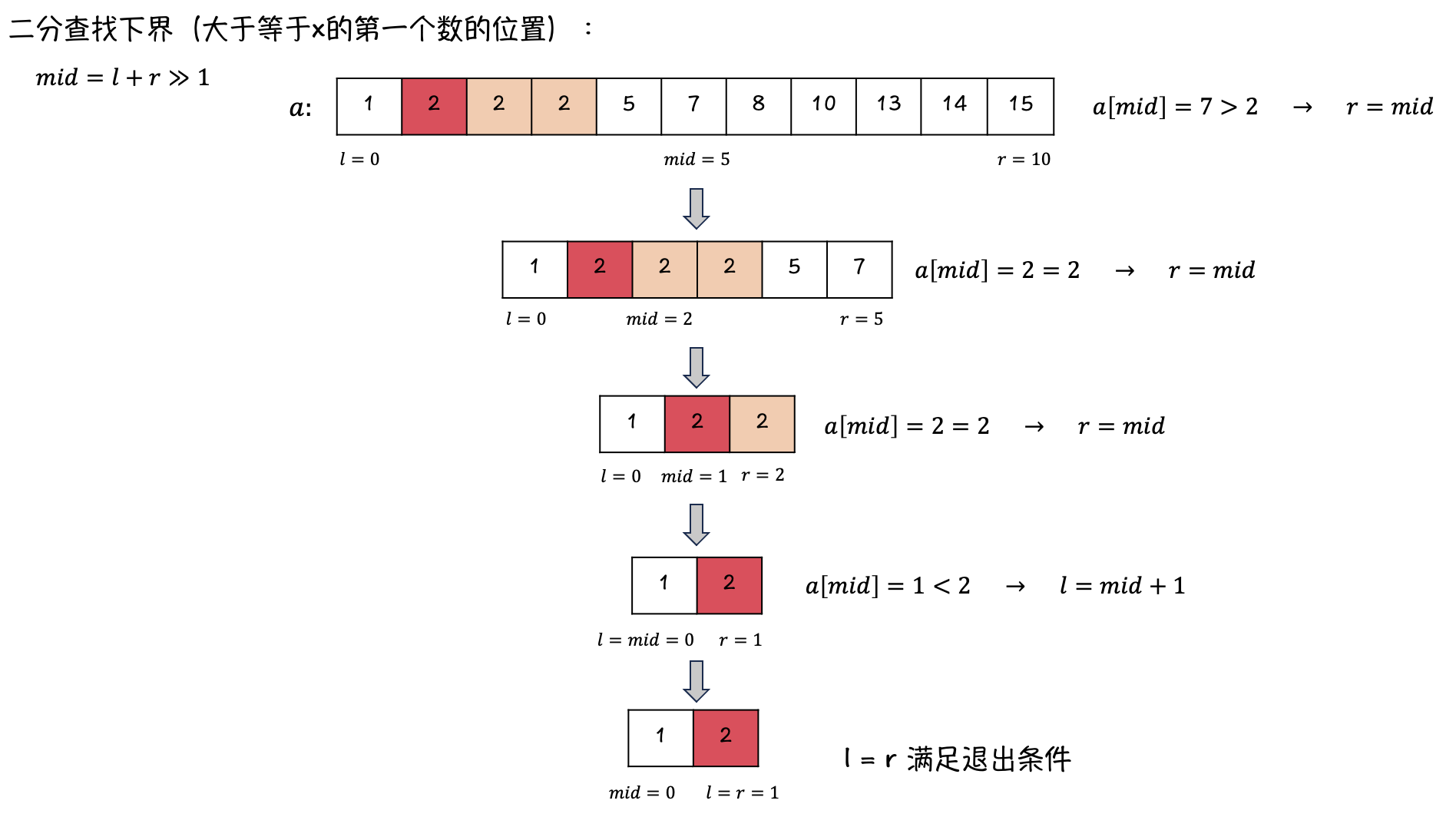
-
在目标数组中找 \(4\):
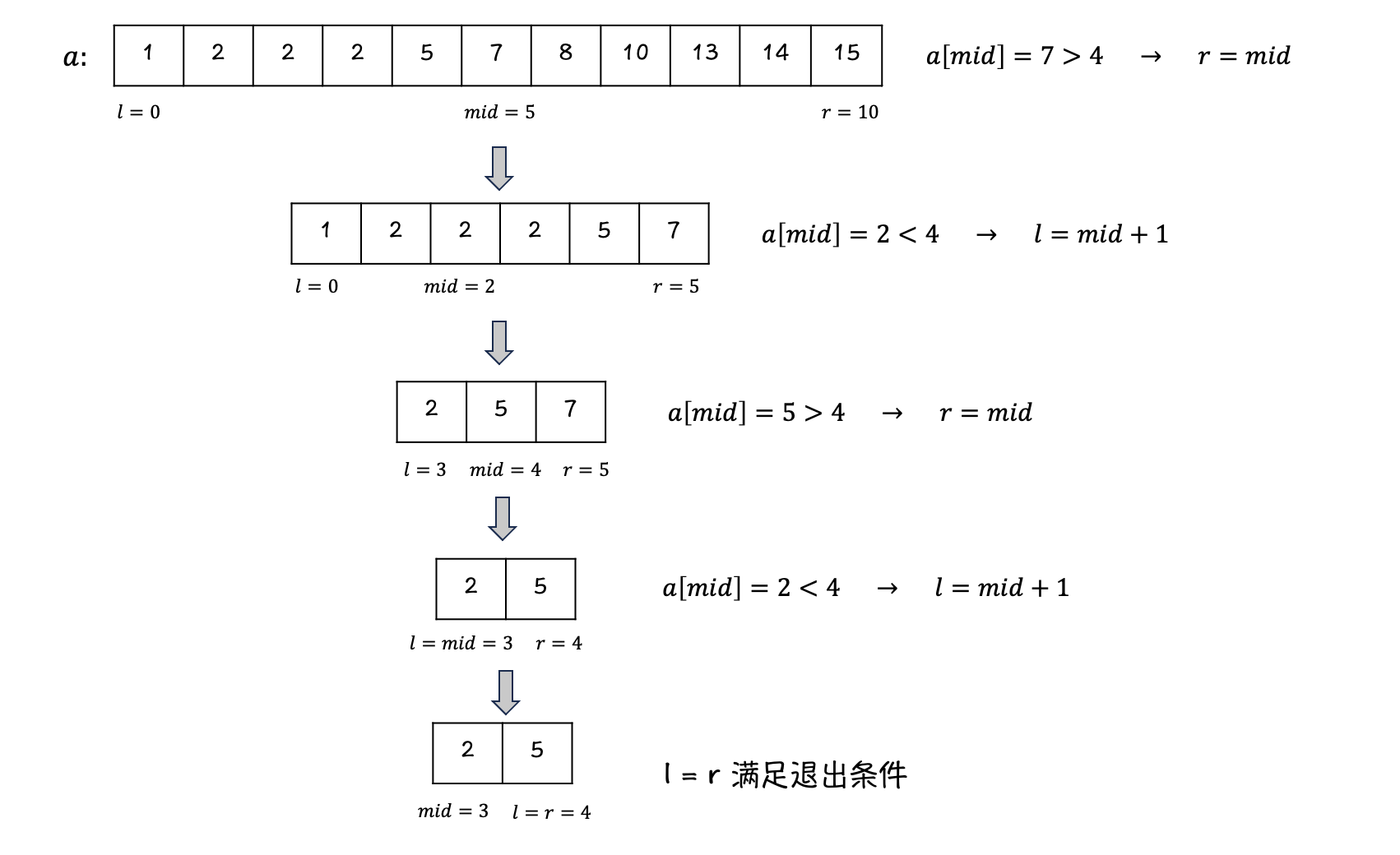
-
可见当找不到目标值时,会找到一个合适的,可以插入目标值的位置的下标
-
二分查找上界
-
在目标数组中找 \(3\):
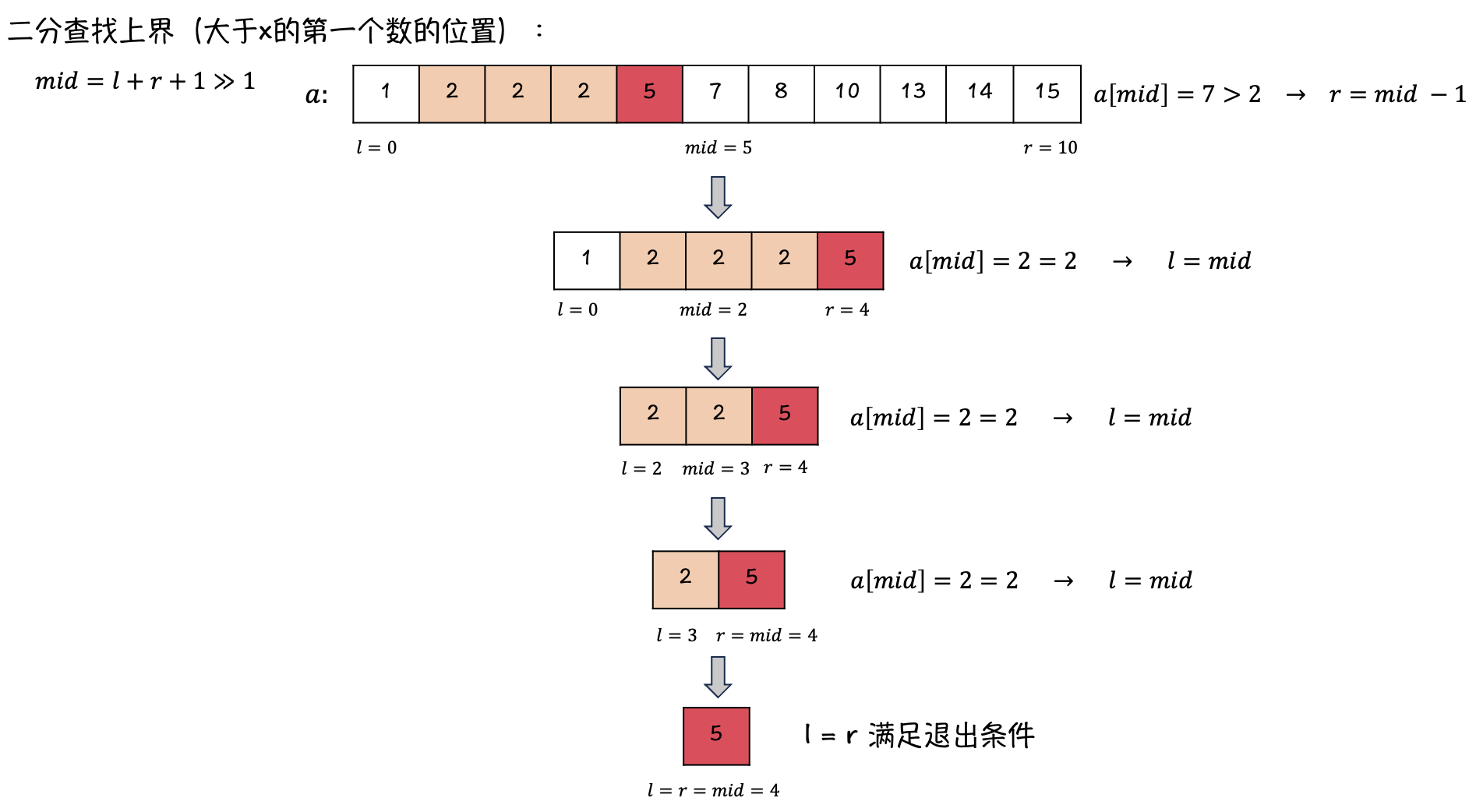
-
同理,如果找不到目标值,也会找到一个合适的、目标值可插入的位置。
-
Tips:
二分查找最终一定可以找到一个“答案”
函数返回上下界是受制于数组上下界的,如果目标值就在数组上界,那么也只会返回数组的上界,而不是目标值上界。
代码(Code)
-
区间分为 \([l,\ mid], [mid + 1,\ r]\):
//向左逼近:查找第一个大于等于给定值的元素 int bsearch_1(int l, int r) { while (l < r) { int mid = l + r >> 1; if (check(mid)) r = mid; else l = mid + 1; } return l; }
-
区间分为 \([l,\ mid - 1], [mid,\ r]\):
//向右逼近:查找最后一个小于等于给定值的元素 int bsearch_2(int l, int r) { while (l < r) { int mid = l + r + 1 >> 1; // 此时为了防止死循环,计算 mid 时需要加 1 if (check(mid)) l = mid; else r = mid - 1; } return l; }
-
浮点数二分:
double d_b_s(double l, double r) { double mid; while (r - l > 1e-(k + 2)) { // k 是题目要求的精确度 mid = (l + r) / 2; if(check()) l = mid; else r = mid; } return l; }
应用(Application)
分巧克力
题目描述
儿童节那天有 \(K\) 位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有 \(N\) 块巧克力,其中第 \(i\) 块是 \(H_i \times W_i\) 的方格组成的长方形。
为了公平起见,小明需要从这 \(N\) 块巧克力中切出 \(K\) 块巧克力分给小朋友们。切出的巧克力需要满足:
形状是正方形,边长是整数。
大小相同。
例如一块 \(6 \times 5\) 的巧克力可以切出 \(6\) 块 \(2 \times 2\) 的巧克力或者 \(2\) 块 \(3 \times 3\) 的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小 \(H_i\) 计算出最大的边长是多少么?
输入格式
第一行包含两个整数 \(N\) 和 \(K\)。\((1 \le N,K \le 10^5)\)。
以下 \(N\) 行每行包含两个整数 \(H_i\) 和 \(W_i\)。\((1 \le H_i,W_i \le 10^5)\)。
输入保证每位小朋友至少能获得一块 \(1 \times 1\) 的巧克力。
输出格式
输出切出的正方形巧克力最大可能的边长。
样例输入
2 10
6 5
5 6
样例输出
2
- 题解:
// C++ Version #include <iostream> #include <algorithm> using namespace std; const int N = 1000010; typedef pair<int, int> pii; int n, m; pii a[N]; bool check(int mid) { int sum = 0; for (int i = 1; i <= n; i ++ ) { auto t = a[i]; sum += t.first / mid * (t.second / mid); } return sum >= m; } int main() { cin >> n >> m; for (int i = 1; i <= n; i ++ ) { int x, y; scanf("%d%d", &x, &y); a[i] = {x, y}; } int l = 0, r = 1e5; while (l < r) { int mid = (l + r + 1) >> 1; if (check(mid)) l = mid; else r = mid - 1; } cout << l << endl; return 0; }
补充(Supplement)
差值查找:
- 将原本的中间值查找条件:\(int\ \ mid = \frac {right + left}{ 2};\)
- 改为:\(int\ \ mid = low + \frac{key - a[low] }{ a[high] - a[low] } * ( high - low );\)
- 即:将上述的比例参数 \(1 / 2\) 改进为 自适应
- 根据关键字在整个有序表中所处的位置,让 \(mid\) 的变化 更靠近 关键字 \(key\),这样也就间接地减少了比较次数


 浙公网安备 33010602011771号
浙公网安备 33010602011771号