可持久化线段树(Persistent Segments Tree)
简介(Introduction)
可持久化线段树(又称函数式线段树)是一种 可持久化数据结构(英语:Persistent data structure)。这种数据结构在普通线段的基础之上支持查询某个历史版本,同时时间复杂度与线段树是同级,空间复杂度相较而言更高。这种数据结构也可被称为***树或主席树。
描述(Description)
-
对序列进行 离散化 ,压缩空间
-
查询一颗区间 \([1, i]\) 的第 \(k\) 小元素,即查询的区间是从第 \(1\) 个元素到第 \(i\) 个元素,对于一个确定的 \(i\) ,
首先建立一颗包含区间 \([1, i]\) 内所有元素的线段树,然后在这棵树上查询第 \(k\) 小元素
-
以序列\(\{321, 123, 5432, 987\}\) 为例:
- 离散化,把序列离散化为 \(\{2, 1, 4, 3\}\),离散化后的元素值是 \(1\sim n\) ,第 \(k\) 小的查找结果
- 查询区间 \([1, i]\) 的第 \(k\) 小元素,线段树 \(R\) 减去线段树 \(L − 1\) ,就即为区间 \([ L , R ]\) 的线段树
- 更新,每次创建的可持久化线段树的绝大部分结点的值是一样的,只有新加入元素有关的部分不同,即:从根结点到叶子结点的一条路径,路径上共有 \(\log n\) 个结点,只需要存储这部分结点即刻。
- 最终 \(n\) 棵线段树的 空间复杂度 :\(O(n\log n)\)
时间复杂度:
- 建树: \(O(nlogn)\)
- \(m\) 次查询:\(O(m\log n)\)
示例(Example)
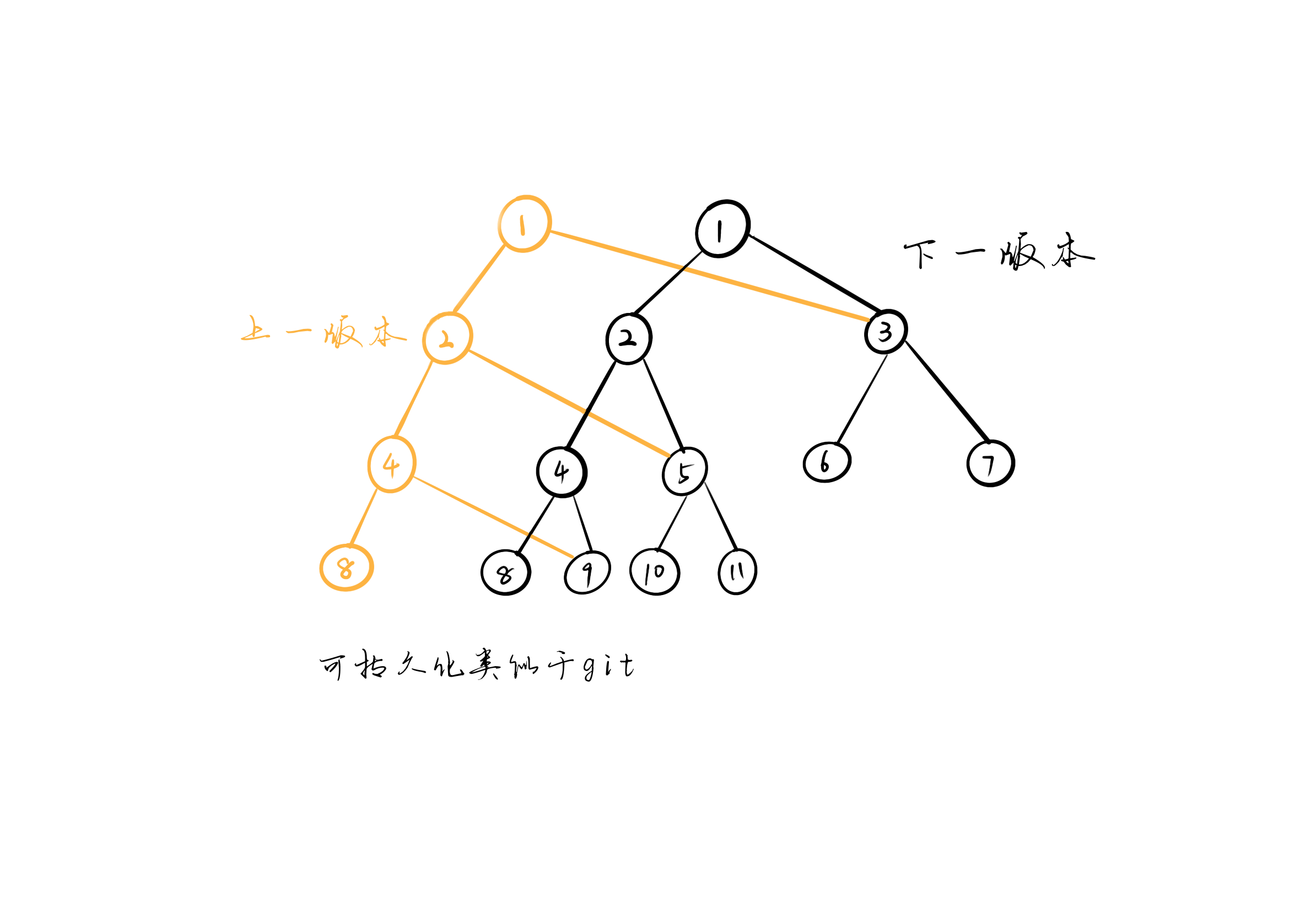
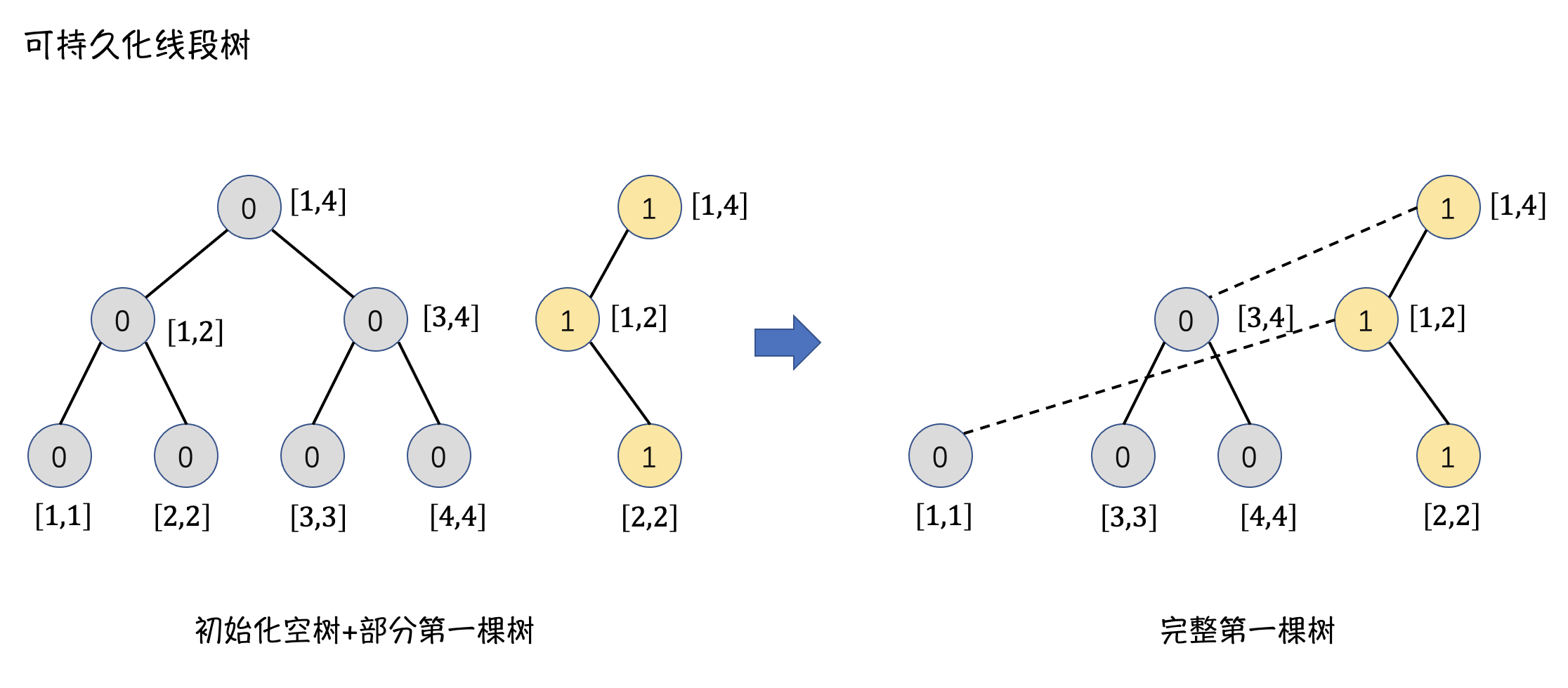
代码(Code)
-
定义结构体:
struct Node { // 定义结点 int L, R, sum; // L 左儿子, R 右儿子,sum[i] 是结点 i 的权值 } tr[MAXN << 5]; // << 4 是乘 16 倍,不够用 -
建树:
const int MAXN = 200010; int cnt = 0; // 用 cnt 标记可以使用的新结点 int a[MAXN], b[MAXN], root[MAXN]; //a[]是原数组,b[]是排序后数组,root[i]记录第i棵线段树的根节点编号 int build(int pl, int pr) { // 初始化一棵空树 int rt = ++ cnt; // cnt 为当前节点编号 tree[rt].sum = 0; int mid = (pl + pr) >> 1; if (pl < pr) { tree[rt].L = build(pl, mid); tree[rt].R = build(mid + 1, pr); } return rt; // 返回当前节点的编号 } -
更新:
int update(int pre, int pl, int pr, int x) { // 建一棵有 logn 个结点的新线段树 int rt = ++ cnt; // 新的结点,下面动态开点 tree[rt].L = tree[pre].L; // 该结点的左右儿子初始化为前一棵树相同位置结点的左右儿子 tree[rt].R = tree[pre].R; tree[rt].sum = tree[pre].sum + 1; // 插入1个数,在前一棵树的相同结点加 1 int mid = (pl + pr) >> 1; if (pl < pr){ // 从根结点往下建 logn 个结点 if (x <= mid) tree[rt].L = update(tree[pre].L, pl, mid, x); // x 出现在左子树,修改左子树 else tree[rt].R = update(tree[pre].R, mid + 1, pr, x); // x 出现在右子树,修改右子树 } return rt; // 返回当前分配使用的新结点的编号 } -
查询:
int query(int u, int v, int pl, int pr, int k) { // 查询区间 [u,v] 第 k 小 if (pl == pr) return pl; // 到达叶子结点,找到第 k 小,pl 是节点编号,答案是 b[pl] int x = tree[tree[v].L].sum - tree[tree[u].L].sum; // 线段树相减 int mid = (pl + pr) >> 1; if (x >= k) return query(tree[u].L, tree[v].L, pl, mid, k); //左儿子数字大于等于k时,说明第k小的数字在左子树 else return query(tree[u].R, tree[v].R, mid+1, pr, k-x); //否则在右子树找第k-x小的数字 }
应用(Application)
第K小数
给定长度为 \(N\) 的整数序列 \(A\),下标为 \(1 \sim N\)。
现在要执行 \(M\) 次操作,其中第 \(i\) 次操作为给出三个整数 \(l_i,r_i,k_i\),求 \(A[l_i],A[l_i+1],…,A[r_i]\) (即 \(A\) 的下标区间 \([l_i,r_i]\))中第 \(k_i\) 小的数是多少。
输入格式
第一行包含两个整数 \(N\) 和 \(M\)。
第二行包含 \(N\) 个整数,表示整数序列 \(A\)。
接下来 \(M\) 行,每行包含三个整数 \(l_i,r_i,k_i\),用以描述第 \(i\) 次操作。
输出格式
对于每次操作输出一个结果,表示在该次操作中,第 \(k\) 小的数的数值。
每个结果占一行。
数据范围
\(N \le 10^5, M \le 10^4,|A[i]| \le 10^9\)
输入样例:
7 3
1 5 2 6 3 7 4
2 5 3
4 4 1
1 7 3
输出样例:
5
6
3
-
题解:
// C++ Version #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #include <vector> using namespace std; const int N = 100010; int n, m; int a[N]; vector<int> nums; int root[N], idx; struct Node { int l, r; int cnt; // 区间内元素的个数 } tr[N << 5]; int find(int x) { return lower_bound(nums.begin(), nums.end(), x) - nums.begin(); } int build(int l, int r) { int p = ++ idx; if (l == r) return p; int mid = l + r >> 1; tr[p].l = build(l, mid); // 递归构建左右子树 tr[p].r = build(mid + 1, r); return p; } int insert(int p, int l, int r, int x) { int q = ++ idx; tr[q] = tr[p]; if (l == r) { tr[q].cnt ++; return q; } int mid = l + r >> 1; if (x <= mid) tr[q].l = insert(tr[p].l, l, mid, x); else tr[q].r = insert(tr[p].r, mid + 1, r, x); tr[q].cnt = tr[tr[q].l].cnt + tr[tr[q].r].cnt; // 当前点的 cnt = 左右子树的 cnt之和 return q; } int query(int q, int p, int l, int r, int k) { if (l == r) return r; int cnt = tr[tr[q].l].cnt - tr[tr[p].l].cnt; int mid = l + r >> 1; if (k <= cnt) return query(tr[q].l, tr[p].l, l, mid, k); else return query(tr[q].r, tr[p].r, mid + 1, r, k - cnt); } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i ++ ) { scanf("%d", &a[i]); nums.push_back(a[i]); } // 离散化 sort(nums.begin(), nums.end()); nums.erase(unique(nums.begin(), nums.end()), nums.end()); root[0] = build(0, nums.size() - 1); for (int i = 1; i <= n; i ++ ) root[i] = insert(root[i - 1], 0, nums.size() - 1, find(a[i])); while (m -- ) { int l, r, k; scanf("%d%d%d", &l, &r, &k); printf("%d\n", nums[query(root[r], root[l - 1], 0, nums.size() - 1, k)]); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号