线段树(Segment Tree)
简介(Introduction)
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数。实际应用时一般还要开
4N的数组以免越界,因此有时需要离散化让空间压缩。
描述(Description)
-
作用:
- 求和
- 修改值
-
五个基本操作:
- \(push\_up\)
- \(push\_down\)
- \(build\_tree\)
- \(query\)
- \(modify\)
-
建树:
-
线段树将每个长度不为 \(1\) 的区间划分成左右两个区间递归求解,把整个线段划分为一个树形结构,通过合并左右两区间信息来求得该区间的信息。这种数据结构可以方便的进行大部分的区间操作。
使用结构体存储节点:
// C++ Version struct Node { int l, r; // 其他属性值(sum,懒惰标记...) } tr[maxn * 4];
-
-
单点查询 / 修改:
- 递归(二分)找到当前区间再目标区间范围内的区间,并对其属性进行修改 / 查询
- 递归(二分)找到当前区间再目标区间范围内的区间,并对其属性进行修改 / 查询
-
区间修改 / 查询:
- 这里引入一个叫做 「懒惰标记」
懒惰标记,是通过延迟对节点信息的更改,从而减少可能不必要的操作次数。每次执行修改时,我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改,但不更新该节点的子节点的信息。实质性的修改则在下一次访问带有标记的节点时才进行。
- 当把区间修改为某个值时,开始只会把标记下传到我们要修改的区间上
- 当查询 / 修改 某个区间后,需要再把这个区间的标记下传到其左右子节点上,并进行对应操作。
- 递归到下面的区间
- 时间复杂度: \({O(\log{n})}\)
示例(Example)
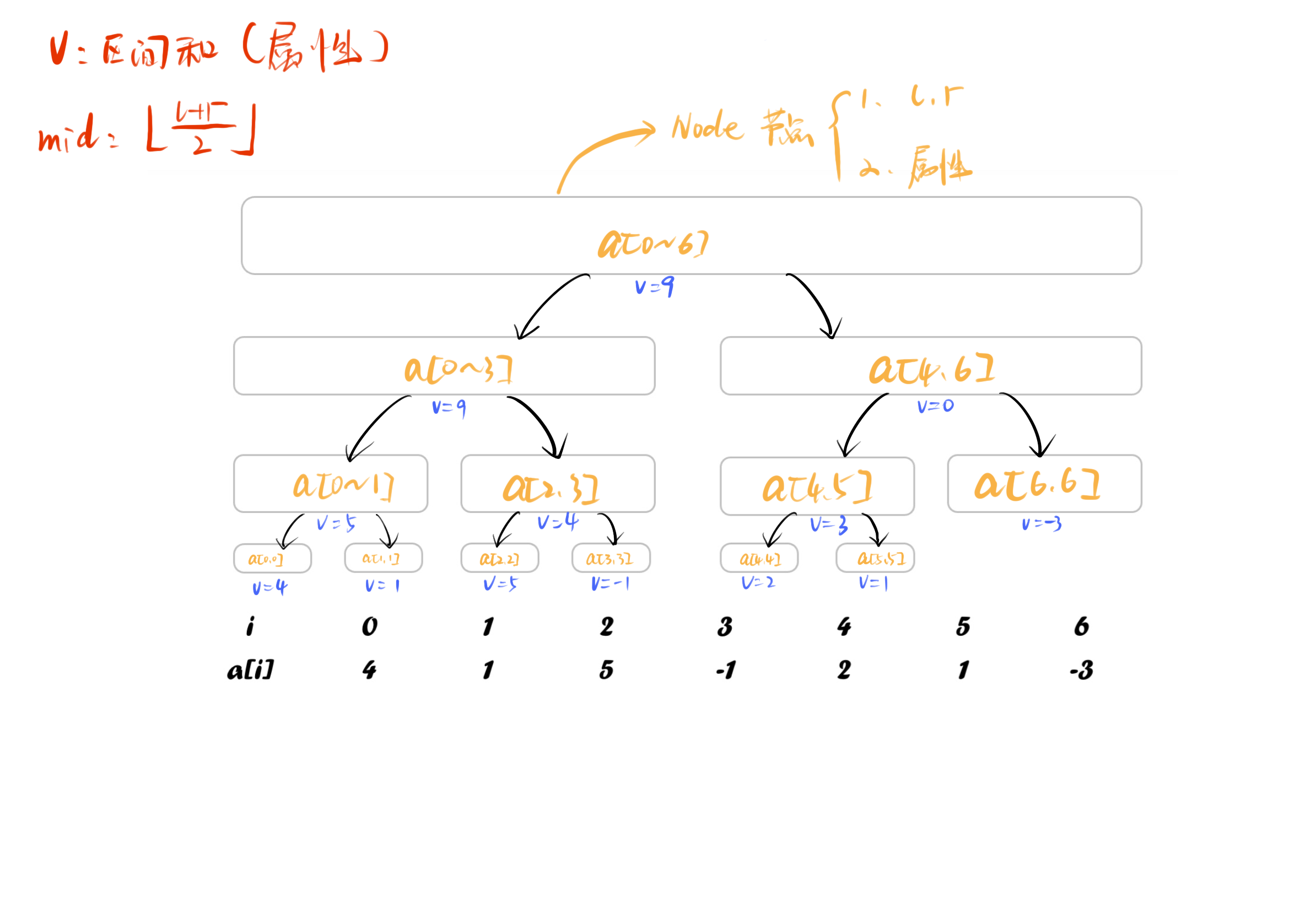
代码(Code)
-
\(push\_up\)
void push_up(int u) { // 子节点向上更新父节点 tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum; } -
\(push\_down\)
void push_down(int u) { // 父节点向下更新子节点 auto &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1]; if (root.add) { left.add += root.add, left.sum += (LL)(left.r - left.l + 1) * root.add; right.add += root.add, right.sum += (LL)(right.r - right.l + 1) * root.add; root.add = 0; } } -
\(build_tree\)
void build(int u, int l, int r) { // 建树 if (l == r) tr[u] = {l, r, w[r], 0}; else { tr[u] = {l, r}; int mid = l + r >> 1; build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r); pushup(u); } } -
\(query\)
long long query(int u, int l, int r) { // 查询区间和 if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum; pushdown(u); int mid = tr[u].l + tr[u].r >> 1; LL sum = 0; if (mid >= l) sum = query(u << 1, l, r); if (mid < r) sum += query(u << 1 | 1, l, r); return sum; } -
\(modify\)
void modify(int u, int l, int r, int c) { // 修改区间和 if (tr[u].l >= l && tr[u].r <= r) { tr[u].sum += (LL)(tr[u].r - tr[u].l + 1) * c; tr[u].add += c; } else { pushdown(u); int mid = tr[u].l + tr[u].r >> 1; if (l <= mid) modify(u << 1, l, r, c); if (r > mid) modify(u << 1 | 1, l, r, c); pushup(u); } } -
实现:
// Java Version class NumArray { public int n; public int[]tree; public int[]nums; public void buildTree(int node,int start,int end){ //终止条件 if(start == end){ tree[node] = nums[start]; return; } int mid = (start + end) >> 1; //计算每个树的节点序号 int left = 2 * node + 1; int right = 2 * node + 2; buildTree(left, start, mid); buildTree(right, mid + 1, end); //将父节点进行子节点求和 tree[node] = tree[left] + tree[right]; } public void updateTree(int node, int start, int end, int index, int val){ if(start == end){ nums[index] = val; tree[node] = val; }else{ int mid = (start + end) >> 1; int left = 2 * node + 1; int right = 2 * node + 2; if(index >= start && index <= mid){ updateTree(left,start,mid,index,val); }else{ updateTree(right,mid+1,end,index,val); } tree[node] = tree[left] + tree[right]; } } public int query(int L,int R,int node,int start,int end){ if( L > end|| R < start) return 0; if(start == end) return tree[node]; if(L <= start && end <= R) return tree[node]; else{ int mid = (start + end) >> 1; int left = 2 * node + 1; int right = 2 * node + 2; int lsum = query(L,R,left,start,mid); int rsum = query(L,R,right,mid+1,end); return lsum + rsum; } } public NumArray(int[] nums) { n = nums.length; this.nums = nums; tree = new int [n * 4]; buildTree(0,0,n - 1); } public void update(int index, int val) { updateTree(0,0,n - 1,index,val); } public int sumRange(int left, int right) { return query(left,right,0,0,n - 1); } }
应用(Application)
最大数
给定一个正整数数列 \(a_1,a_2,…,a_n\),每一个数都在 \(0 \sim p-1\) 之间。
可以对这列数进行两种操作:
- 添加操作:向序列后添加一个数,序列长度变成 \(n+1\);
- 询问操作:询问这个序列中最后 \(L\) 个数中最大的数是多少。
程序运行的最开始,整数序列为空。
一共要对整数序列进行 \(m\) 次操作。
写一个程序,读入操作的序列,并输出询问操作的答案。
输入格式
第一行有两个正整数 \(m,p\),意义如题目描述;
接下来 \(m\) 行,每一行表示一个操作。
如果该行的内容是
Q L,则表示这个操作是询问序列中最后 \(L\) 个数的最大数是多少;如果是
A t,则表示向序列后面加一个数,加入的数是 \((t+a)\ mod\ p\)。其中,\(t\) 是输入的参数,\(a\) 是在这个添加操作之前最后一个询问操作的答案(如果之前没有询问操作,则 \(a=0\))。第一个操作一定是添加操作。对于询问操作,\(L>0\) 且不超过当前序列的长度。
输出格式
对于每一个询问操作,输出一行。该行只有一个数,即序列中最后 \(L\) 个数的最大数。
数据范围
\(1 \le m \le 2 \times 10^5\),
\(1 \le p \le 2 \times 10^9\),
\(0 \le t < p\)
输入样例:
10 100
A 97
Q 1
Q 1
A 17
Q 2
A 63
Q 1
Q 1
Q 3
A 99
输出样例:
97
97
97
60
60
97
样例解释
最后的序列是 \(97,14,60,96\)。
-
题解:
// C++ Version #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long LL; const int N = 200010; int n, m, p; struct Node { int l, r; int v; } tr[N * 4]; int pushup(int u) { // 更新父节点的区间最大值 tr[u].v = max(tr[u << 1 | 1].v, tr[u << 1].v); } int query(int u, int l, int r) { // 查询区间[l, r]中的最大值 if (tr[u].l >= l && tr[u].r <= r) return tr[u].v; int mid = tr[u].l + tr[u].r >> 1; int v = 0; if (mid >= l) v = query(u << 1, l, r); if (mid < r) v = max(v, query(u << 1 | 1, l, r)); return v; } // u:当前节点,x:目标节点, v:修改后的节点值 void modify(int u, int x, int v) { if (tr[u].l == x && tr[u].r == x) tr[u].v = v; else { int mid = tr[u].l + tr[u].r >> 1; if (x <= mid) modify(u << 1, x, v); else modify(u << 1 | 1, x, v); pushup(u); } } void build(int u, int l, int r) { tr[u] = {l, r}; if (l == r) return; int mid = l + r >> 1; build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r); } int main() { scanf("%d%d", &m, &p); build(1, 1, m); int x; char op[2]; int last = 0; while (m -- ) { scanf("%s%d", op, &x); if (*op == 'Q') { last = query(1, n - x + 1, n); printf("%d\n", last); } else { modify(1, n + 1, ((LL)last + x) % p); n ++ ; } } return 0; }
一个简单的整数问题2
给定一个长度为 \(N\) 的数列 \(A\),以及 \(M\) 条指令,每条指令可能是以下两种之一:
C l r d,表示把 \(A[l],A[l+1],…,A[r]\) 都加上 \(d\)。Q l r,表示询问数列中第 \(l \sim r\) 个数的和。对于每个询问,输出一个整数表示答案。
输入格式
第一行两个整数 \(N,M\)。
第二行 \(N\) 个整数 \(A[i]\)。
接下来 \(M\) 行表示 \(M\) 条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
\(1 \le N,M \le 10^5\),
\(|d| \le 10000\),
\(|A[i]| \le 10^9\)
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
输出样例:
4
55
9
15
-
题解:
// C++ Version 线段树解法 #include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long LL; const int N = 100010; int n, m; int w[N]; struct Node { int l, r; LL sum, add; } tr[N * 4]; void pushup(int u) { tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum; } void pushdown(int u) { auto &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1]; if (root.add) { left.add += root.add, left.sum += (LL)(left.r - left.l + 1) * root.add; right.add += root.add, right.sum += (LL)(right.r - right.l + 1) * root.add; root.add = 0; } } void build(int u, int l, int r) { if (l == r) tr[u] = {l, r, w[r], 0}; else { tr[u] = {l, r}; int mid = l + r >> 1; build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r); pushup(u); } } void modify(int u, int l, int r, int c) { if (tr[u].l >= l && tr[u].r <= r) { tr[u].sum += (LL)(tr[u].r - tr[u].l + 1) * c; tr[u].add += c; } else { pushdown(u); int mid = tr[u].l + tr[u].r >> 1; if (l <= mid) modify(u << 1, l, r, c); if (r > mid) modify(u << 1 | 1, l, r, c); pushup(u); } } LL query(int u, int l, int r) { if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum; pushdown(u); int mid = tr[u].l + tr[u].r >> 1; LL sum = 0; if (mid >= l) sum = query(u << 1, l, r); if (mid < r) sum += query(u << 1 | 1, l, r); return sum; } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]); build(1, 1, n); char op[2]; int l, r, d; while (m -- ) { scanf("%s%d%d", op, &l, &r); if (*op == 'C') { scanf("%d", &d); modify(1, l, r, d); } else printf("%lld\n", query(1, l, r)); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号