树状数组(Fenwick Tree)
简介(Introduction)
树状数组 或 二叉索引树 (Binary Indexed Tree),最早由 Peter M. Fenwick 于1994年以 A New Data Structure for Cumulative Frequency Tables 为题发表在 SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题,现多用于高效计算数列的前缀和, 区间和。
描述(Description)
-
作用:
- 快速求前缀和
- 修改某一个数
-
核心:用 树 来维护 前缀和
-
对于任意 \(\large{x}\) 均可由二进制数表示,即:\(\large{x = 2^{i_1} + 2^{i_2} +···+ 2^{i_k}}\)
-
将 \(\large{x}\) 分为以下区间:
\[(x - 2^{i_1}, x] \]\[(x - 2^{i_1} - 2^{i_2}, x - 2^{i_1}] \]\[\dots \]\[(0,x - 2^{i_1} - 2^{i_2}, x - 2^{i_1}-···-x - 2^{i_{k - 1}}] \] -
对于每个区间 \(\displaystyle{(l, r]}\) ,其长度一定是r二进制表示下最后一个1所对应的次幂
-
等价于 \(\displaystyle{[r - lowbit(r) +1,r]}\) 。同时用一个数组 \(c[r]\) 来表示这个区间的和。
-
得:\(\large{c[r] = \sum{^{x}_{i = x - lowbit(x) + 1} a[i]}}\)
-
时间复杂度:
- 树初始化:
- 朴素:把 \(n\) 个数各自加入树状数组。\(O(nlogn)\)
- 前缀和:\(O(n)\)
- 快速求前缀和:\(O(log n)\)
- 修改某一个数:\(O(log n)\)
- 树初始化:
示例(Example)
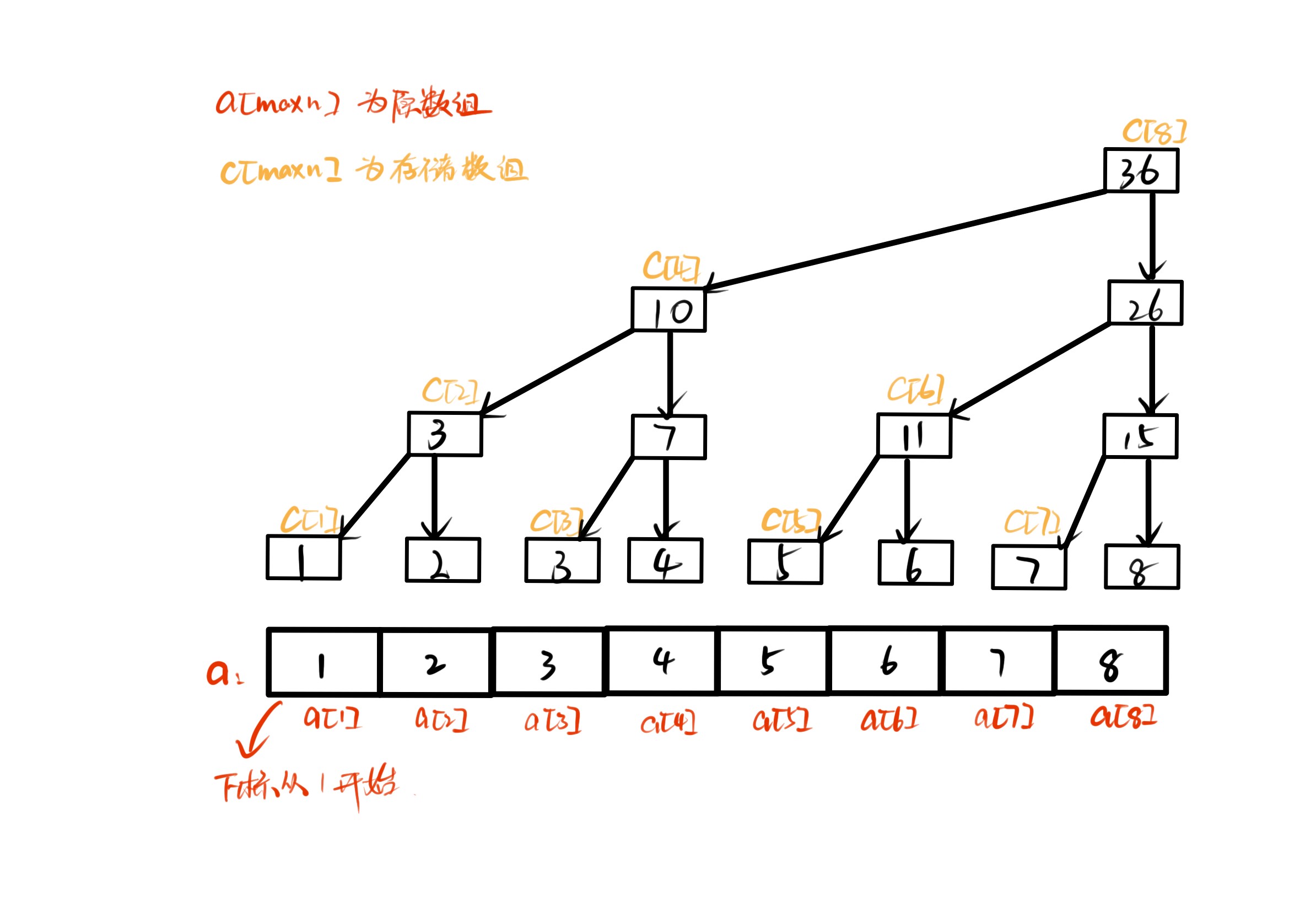
代码(Code)
-
\(lowbit\) 操作:
int lowbit(int x) { return x & -x; }
-
初始化:
void init() { for (int i = 1; i <= n; i ++ ) { pre[i] = pre[i - 1] + a[i]; // pre 为前缀和数组 tr[i] = pre[i] - pre[i - lowbit(i)]; } }
-
查询前缀和:
int sum(int x) { int res = 0; for (int i = x; i; i -= lowbit(i)) res += tr[i]; return res; }
-
单点增加:
int add(int x, int c) { for (int i = x; i <= n; i += lowbit(i)) tr[i] += c; }
应用(Application)
楼兰图腾
在完成了分配任务之后,西部 \(314\) 来到了楼兰古城的西部。
相传很久以前这片土地上(比楼兰古城还早)生活着两个部落,一个部落崇拜尖刀(
V),一个部落崇拜铁锹(∧),他们分别用V和∧的形状来代表各自部落的图腾。西部 \(314\) 在楼兰古城的下面发现了一幅巨大的壁画,壁画上被标记出了 \(n\) 个点,经测量发现这 \(n\) 个点的水平位置和竖直位置是两两不同的。
西部 \(314\) 认为这幅壁画所包含的信息与这 \(n\) 个点的相对位置有关,因此不妨设坐标分别为 \((1,y_1),(2,y_2),…,(n,y_n)\),其中 \(y_1 \sim y_n\) 是 \(1\) 到 \(n\) 的一个排列。
西部 \(314\) 打算研究这幅壁画中包含着多少个图腾。
如果三个点 \((i,y_i),(j,y_j),(k,y_k)\) 满足 \(1 \le i < j < k \le n\) 且 \(y_i > y_j, y_j < y_k\),则称这三个点构成
V图腾;如果三个点 \((i,y_i),(j,y_j),(k,y_k)\) 满足 \(1 \le i < j< k \le n\) 且 \(y_i < y_j, y_j > y_k\),则称这三个点构成
∧图腾;西部 \(314\) 想知道,这 \(n\) 个点中两个部落图腾的数目。
因此,你需要编写一个程序来求出
V的个数和∧的个数。输入格式
第一行一个数 \(n\)。
第二行是 \(n\) 个数,分别代表 \(y_1,y_2,…,y_n\)。
输出格式
两个数,中间用空格隔开,依次为
V的个数和∧的个数。数据范围
对于所有数据,\(n \le 200000\),且输出答案不会超过 \(int64\)。
\(y_1 \sim y_n\) 是 \(1\) 到 \(n\) 的一个排列。
输入样例:
5
1 5 3 2 4
输出样例:
3 4
-
分析:
- 若 \(1\sim n\) 中 \(y_i\) 为最下面的情况,统计 \(y_i\) 左边和右边各有多少数大于它
- 根据 乘法原理 把两个数相乘即可得到 \(y_i\) 在最下面的情况时对答案的贡献
-
题解:
// C++ Version #include <cstring> #include <cstdio> using namespace std; typedef long long ll const int N = 200010; int n; int a[N]; int tr[N]; int high[N], low[N]; int lowbit(int x) { return x & -x; } int add(int x) { for (int i = x; i <= n; i += lowbit(i)) tr[i] ++ ; } int sum(int x) { int res = 0; for (int i = x; i; i -= lowbit(i)) res += tr[i]; return res; } int main() { scanf("%d", &n); for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]); for (int i = 1; i <= n; i ++ ) { int t = a[i]; high[i] = sum(n) - sum(t); low[i] = sum(t - 1); add(t); } memset(tr, 0, sizeof tr); llres1 = 0, res2 = 0; for (int i = n; i; i -- ) { int t = a[i]; res1 += 1ll * high[i] * (sum(n) - sum(t)); res2 += 1ll * low[i] * sum(t - 1); add(t); } printf("%lld %lld\n", res1, res2); return 0; }
一个简单的整数问题
给定长度为 \(N\) 的数列 \(A\),然后输入 \(M\) 行操作指令。
第一类指令形如
C l r d,表示把数列中第 \(l \sim r\) 个数都加 \(d\)。第二类指令形如
Q x,表示询问数列中第 \(x\) 个数的值。对于每个询问,输出一个整数表示答案。
输入格式
第一行包含两个整数 \(N\) 和 \(M\)。
第二行包含 \(N\) 个整数 \(A[i]\)。
接下来 \(M\) 行表示 \(M\) 条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
\(1 \le N,M \le 10^5\),
\(|d| \le 10000\),
\(|A[i]| \le 10^9\)
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4
Q 1
Q 2
C 1 6 3
Q 2
输出样例:
4
1
2
5
-
分析:先做一遍差分,然后利用树状数组求区间和
-
题解:
// C++ Version #include <cstdio> #include <cstring> using namespace std; typedef long long ll; const int N = 100010; int n, m; int a[N]; ll tr[N]; int lowbit(int x) { return x & -x; } void add(int x, int c) { for (int i = x; i <= n; i += lowbit(i)) tr[i] += c; } ll sum(int x) { ll res = 0; for (int i = x; i; i -= lowbit(i)) res += tr[i]; return res; } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]); for (int i = 1; i <= n; i ++ ) add(i, a[i] - a[i - 1]); // 差分 while (m -- ) { char op[2]; int l, r, d; scanf("%s%d", op, &l); if (*op == 'C') { scanf("%d%d", &r, &d); add(l, d), add(r + 1, -d); } else { printf("%lld\n", sum(l)); // 重新求前缀和 } } return 0; }
一个简单的整数问题2
给定一个长度为 \(N\) 的数列 \(A\),以及 \(M\) 条指令,每条指令可能是以下两种之一:
C l r d,表示把 \(A[l],A[l+1],…,A[r]\) 都加上 \(d\)。Q l r,表示询问数列中第 \(l \sim r\) 个数的和。对于每个询问,输出一个整数表示答案。
输入格式
第一行两个整数 \(N,M\)。
第二行 \(N\) 个整数 \(A[i]\)。
接下来 \(M\) 行表示 \(M\) 条指令,每条指令的格式如题目描述所示。
输出格式
对于每个询问,输出一个整数表示答案。
每个答案占一行。
数据范围
\(1 \le N,M \le 10^5\),
\(|d| \le 10000\),
\(|A[i]| \le 10^9\)
输入样例:
10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4
输出样例:
4
55
9
15
- 题解:
// C++ Version 树状数组解法 #include <cstdio> #include <cstring> using namespace std; typedef long long ll; const int N = 100010; int n, m; int a[N]; ll tr1[N]; ll tr2[N]; int lowbit(int x) { return x & -x; } void add(ll tr[], int x, ll c) { for (int i = x; i <= n; i += lowbit(i)) tr[i] += c; } ll sum(ll tr[], int x) { ll res = 0; for (int i = x; i; i -= lowbit(i)) res += tr[i]; return res; } ll prefix_sum(int x) { return sum(tr1, x) * (x + 1) - sum(tr2, x); } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i ++ ) { scanf("%d", &a[i]); int b = a[i] - a[i - 1]; add(tr1, i, b); add(tr2, i, (ll)b * i); } while (m -- ) { char op[2]; int l, r, d; scanf("%s%d%d", op, &l, &r); if (*op == 'Q') { printf("%lld\n", prefix_sum(r) - prefix_sum(l - 1)); } else { scanf("%d", &d); add(tr1, l, d), add(tr2, l, l * d); add(tr1, r + 1, -d), add(tr2, r + 1, (r + 1) * -d); } } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号