外部排序(External Sort)
简介(Introduction)
外部排序 指的是 大文件 的排序,即待排序的记录存储在外存储器上,待排序的文件无法一次装入内存,需要在内存和外部存储器之间进行多次数据交换,以达到排序整个文件的目的。
描述(Description)
- 外排序分为两个步骤:
- 预处理:
- 首先,根据可用内存的大小,将外存上含有 \(n\) 个纪录的文件分成若干长度为 \(t\) 的子文件(或段)
- 其次,利用内部排序的方法,对每个子文件的 \(t\) 个纪录进行内部排序
- 这些经过排序的子文件(段)通常称为顺串 \((run)\),顺串生成后即将其写入外存。这样在外存上就得到了 \(m\) 个顺串 \((m=[n/t])\)
- 合并排序:对这些顺串进行归并,使顺串的长度逐渐增大,直到所有的待排序的记录成为一个顺串为止。
- 预处理:
由于 \(外部排序的总时间=内部排序所需的时间+外存信息读写的时间+内部归并所需的时间\)
外部信息读写的时间远远大于内部排序和内部归并的时间,因此应着力减少 \(I/O\) 次数。增加归并路数,可减少归并趟数,进而减少总的磁盘 \(I/O\) 次数。
-
优化顺序:
- 二路归并,由于硬盘的读写速度比内存要慢的多,上述方法较慢,考虑 \(k\) 路归并
- \(k\) 路归并, \(k\) 不是越大越好,\(k\) 与内部排序需要时间成正比。考虑减少初始顺串的数量 \(M\)
- 置换—选择算法,使用 败者树 和 堆排序 实现,得到多个长度不等的初始归并段。考虑结合哈夫曼树设置归并顺序,减少对外存的访问次数
- 最佳归并树 —— 置换选择算法+哈夫曼树+多路归并+败者树
-
优化后外部排序执行顺序:
- 第一步,序置换选择排序,用来生成尽可能长的数据串
- 第二步,\(k\) 路归并,将所有的顺段都归并成一路,在归并的过程用 \(Huffman\ \ tree\) 来优化(每次挑长度最小的顺段)进行归并,归并用 败者树 来实现
二路归并
- Two-Way Merge —— 二路归并
对 \(n\) 个有序的文件进行 两两归并,过程与归并排序相同
每次由 \(n\) 个归并段,得到 \(\lceil n / 2 \rceil\) 个归并段
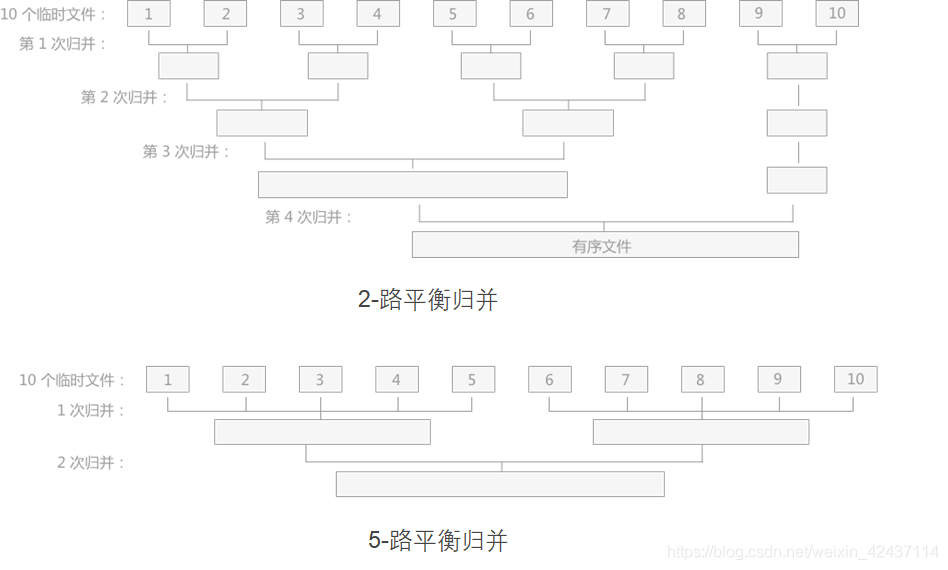
\(k\) 路归并
- K-Way Merge —— \(k\) 路归并
- \(k\) 路归并是每次将 \(k\) 个顺串合并成一个排好序的顺串
- 采用选择树的方法来实现 \(k\) 路归并
- 选择树类型:
- 胜者树
- 败者树(常用)
- 选择树类型:
- 一般情况下,对 \(m\) 个初始顺串进行 \(k\) 路归并,归并趟数为:\(\log_km\)
- 增加每次归并的顺串数量 k 可以减少归 并趟数
Tips:若 \(k\) 的值无限增加,虽然会减少归并次数,但是会增加内部排序时间
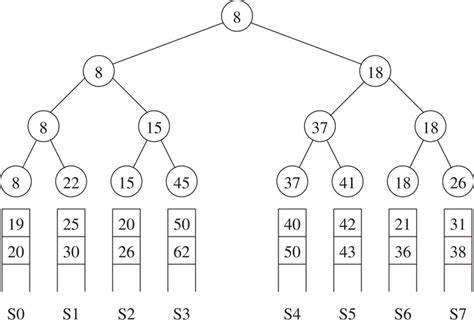
- 胜者树(Winner Tree):
- 定义:
- 胜者树是一颗 完全二叉树
- 胜者树的叶子结点保存我们的一个输入缓冲区(每个选手的值)
- 胜者树的非叶子节点保存当前比较的胜者的输入缓冲区的指针
- 胜者树的 根节点 为冠军
- 优点:如果某个选手(叶子节点)的值改变了,只需要沿着从该节点到根节点的路径修改这一颗树,不用改变其他结果
- 定义:
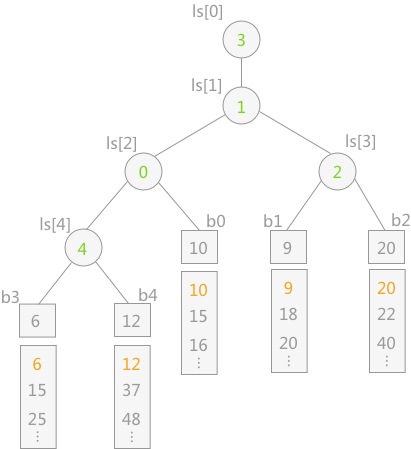
- 败者树(Loser Tree):
- 定义:
- 败者树是一颗完全二叉树(胜者树的一种变体)
- 败者树的叶子结点保存的是我们的输入缓冲区(每个选手的值)
- 败者树的非叶子结点保存我们的当前的比较中败者的对应的输入缓冲区的指针(比较的两个数,大者为失败、小的为胜利者)
- 败者树根保存亚军,根上面还有一个节点 保存冠军
- 定义:
胜者树 和 败者树 的区别:
- 胜者树中的非终端结点中存储的是胜利的一方,败者树中的非终端结点存储的是失败的一方。但在比较过程中,都是拿胜者去比较。
- 败者树重构只是与该结点的父结点的记录有关,而胜者树重构还与该结点的兄弟结点有关。
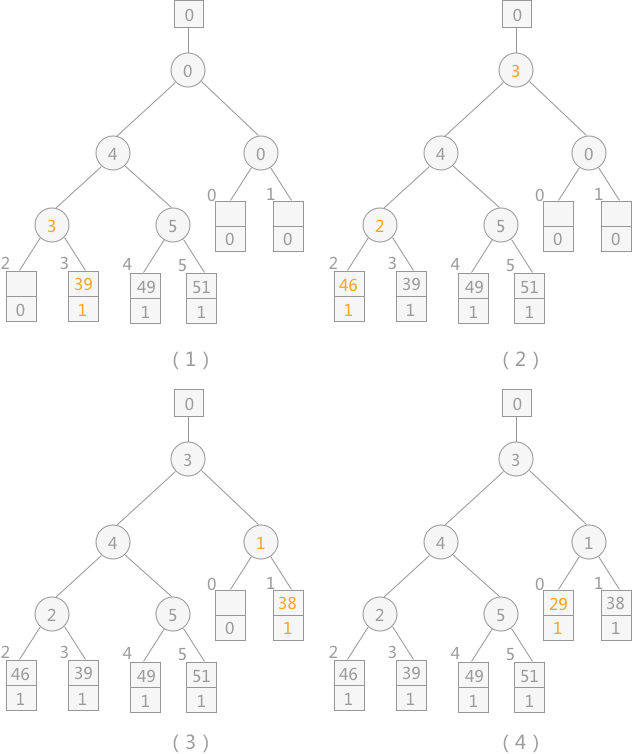
置换—选择排序算法
- Replacement Selection Sort Algorithm —— 置换—选择排序算法
- 如果要想减小 \(m\) 的值,在外部文件总的记录数 \(n\) 值一定的情况下,只能增加每个归并段中所包含的记录数 \(l\)
- 而对于初始归并段的形成,因为所有的内部排序所有的记录都存在于内存中,而内存的可使用的空间有限,如果增加 \(l\) 的值,内存无法存放,可以使用 置换—选择排序算法
- 步骤:
- 首先从初始文件中输入 \(6\) 个记录到内存工作区中;
- 从内存工作区中选出关键字最小的记录,将其记为 \(MINIMAX\) 记录;
- 然后将 \(MINIMAX\) 记录输出到归并段文件中;
- 此时内存工作区中还剩余 \(5\) 个记录,若初始文件不为空,则从初始文件中输入下一个记录到内存工作区中;
- 从内存工作区中的所有比 \(MINIMAX\) 值大的记录中选出值最小的关键字的记录,作为新的 \(MINIMAX\) 记录;(使用败者树或者堆排序实现)
- 重复过程 \(3—5\),直至在内存工作区中选不出新的 \(MINIMAX\) 记录为止,由此就得到了一个初始归并段;
- 重复 \(2—6\),直至内存工作为空,由此就可以得到全部的初始归并段。
最佳归并树
- Optimal Merge Tree —— 最佳归并树
通过以构建 哈夫曼树 的方式构建 归并树,使其对读写外存的次数降至最低( \(k-\)路平衡归并,需要选取合适的 \(k\) 值,构建哈夫曼树作为归并树),称此归并树为 最佳归并树。
- 对于减少访问外存的次数的问题,等同于使 \(k-\)路归并所构成的 \(k\) 叉树的带权路径长度最短。
- 若使树的带权路径长度 \((WPL)\) 最短,即:构造 哈夫曼树
- 磁盘 \(I/O\) 次数 \(= WPL * 2\)
归并树是否需要添加 虚段:
- 对于 \(k–\)路平衡归并来说,若 \((m-1)\ mod\ (k-1) = 0\),则不需要增加虚段
- 否则需加:\(k\ -[\ (m-1)\ mod \ (k-1)] - 1\) 个虚段
示例(Example)
-
胜者树:
-
败者树:
-
置换选择排序
-
\(k\) 路归并:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号