KMP Algorithm
简介(Introduction)
\(KMP\) 算法是一种改进的字符串匹配算法,由 D.E.Knuth,J.H.Morris 和 V.R.Pratt 提出的,因此人们称它为 克努特—莫里斯—普拉特操作(简称 \(KMP\) 算法)
\(KMP\) 算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。
描述(Description)
-
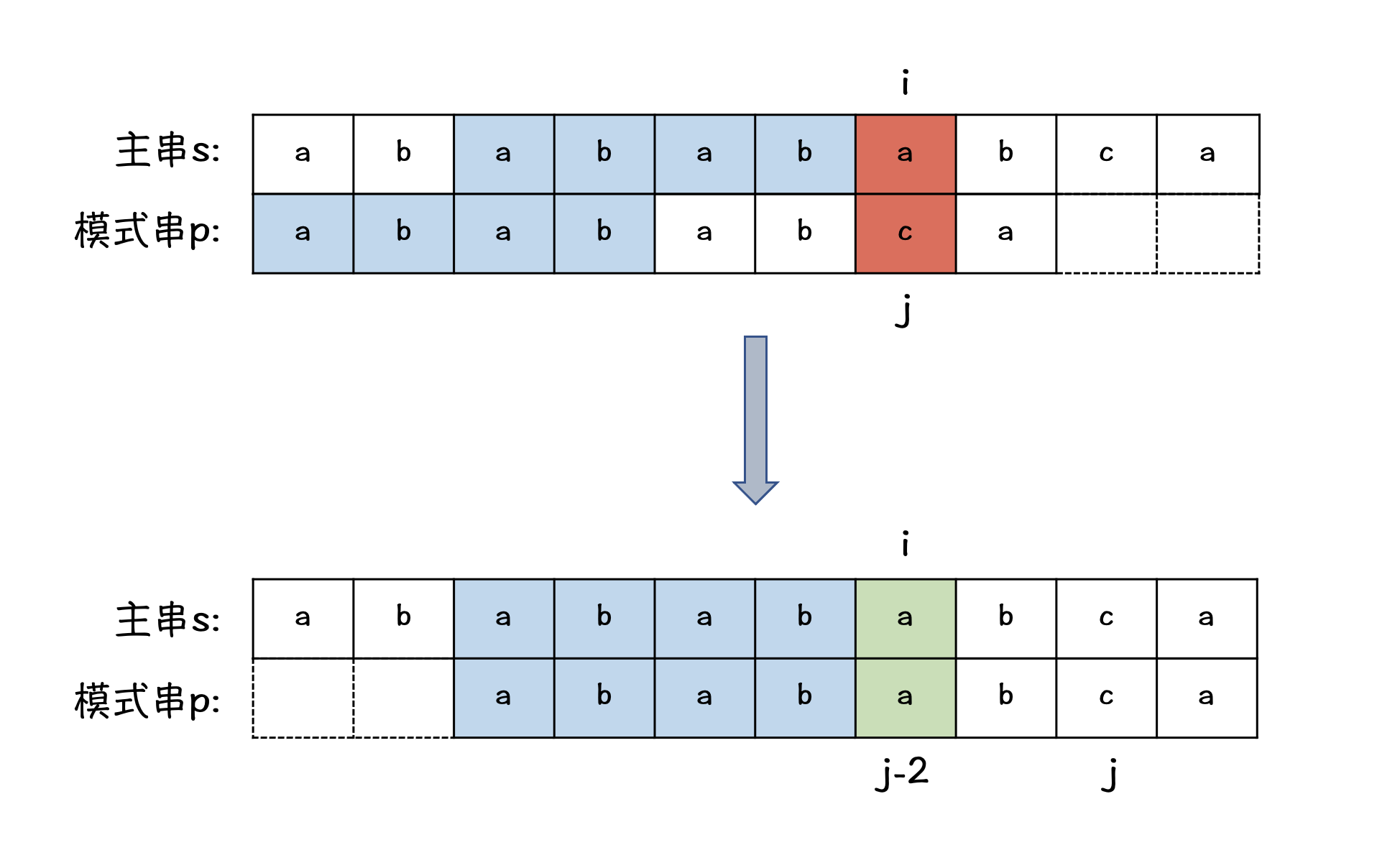
当 主串 中第 \(i\) 个字符,与 模式串 中第 \(j\) 个字符匹配失败,但是有 成功的部分 \(ababab\),且 \(ababab\) 有 最长的成功的部分 \(abab\) 长度为:\(4\),所以,只要移动两格能继续匹配:主串 第 \(i - 4 \sim i - 1\) 与 模式串 第 \(1 \sim 4\) 完全匹配
-
当 主串 第 \(i\) 个字符与 模式串 第 \(j\) 个字符匹配失败时,经过移动,可以使 主串 中 \(i- k \sim i - 1\) 与 模式串 中 \(1 \sim k\ \ \ (k < j)\) 相等,即完成匹配。
得到关系:\(p_1\ p_2\ \dots \ p_{k−1} = s_{i−(k−1)}\ s_{i−(k−2)}\ \dots \ s_{i−1}\)
- 并且 \(k\) 为所有满足条件的最大 \(k\) —— 最长的成功的部分
而我们已经有之前匹配完成的部分:\(p_{j−(k−1)}\ p_{j−(k−2)} \dots p_{j−1} = s_{i−(k−1)}\ s_{i−(k−2)}\ \dots\ s_{i−1}\)
对比两式可得:\(p_1 \ p_2 \ \dots \ p_{k−1} = p_{j−(k−1)}\ p_{j−(k−2)} \ \dots \ p_{j−1}\) —— 成功部分中最长的成功的部分对应的等式
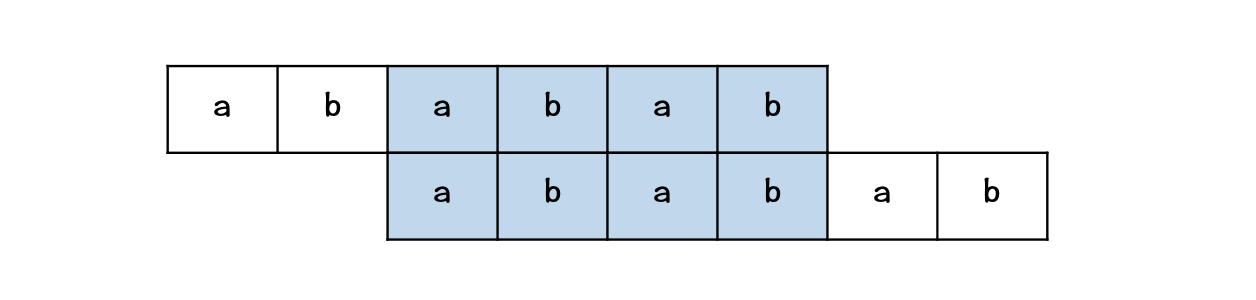
\(ne\) 数组定义如下
\(ne[i] = k\) ,前 \(i\) 个字符 ( \(i\) 为已经匹配成功的长度),后缀 与 前缀 相等的 最大长度 \(max_{len} = k\)(非平凡)
\(ne[1]\) 默认为 \(0\)
\(ne[j] = k\),\(k\) 表示:可以从 模式串 \(p\) 的第 \(k\) 位开始继续向后比较
当 不存在 成功部分自身的成功部分时,即:\(ne[j] == 0\),则重新比较
- 每次的匹配就能通过 \(ne\) 的值快速找到继续匹配的位置,或者直接下一轮。
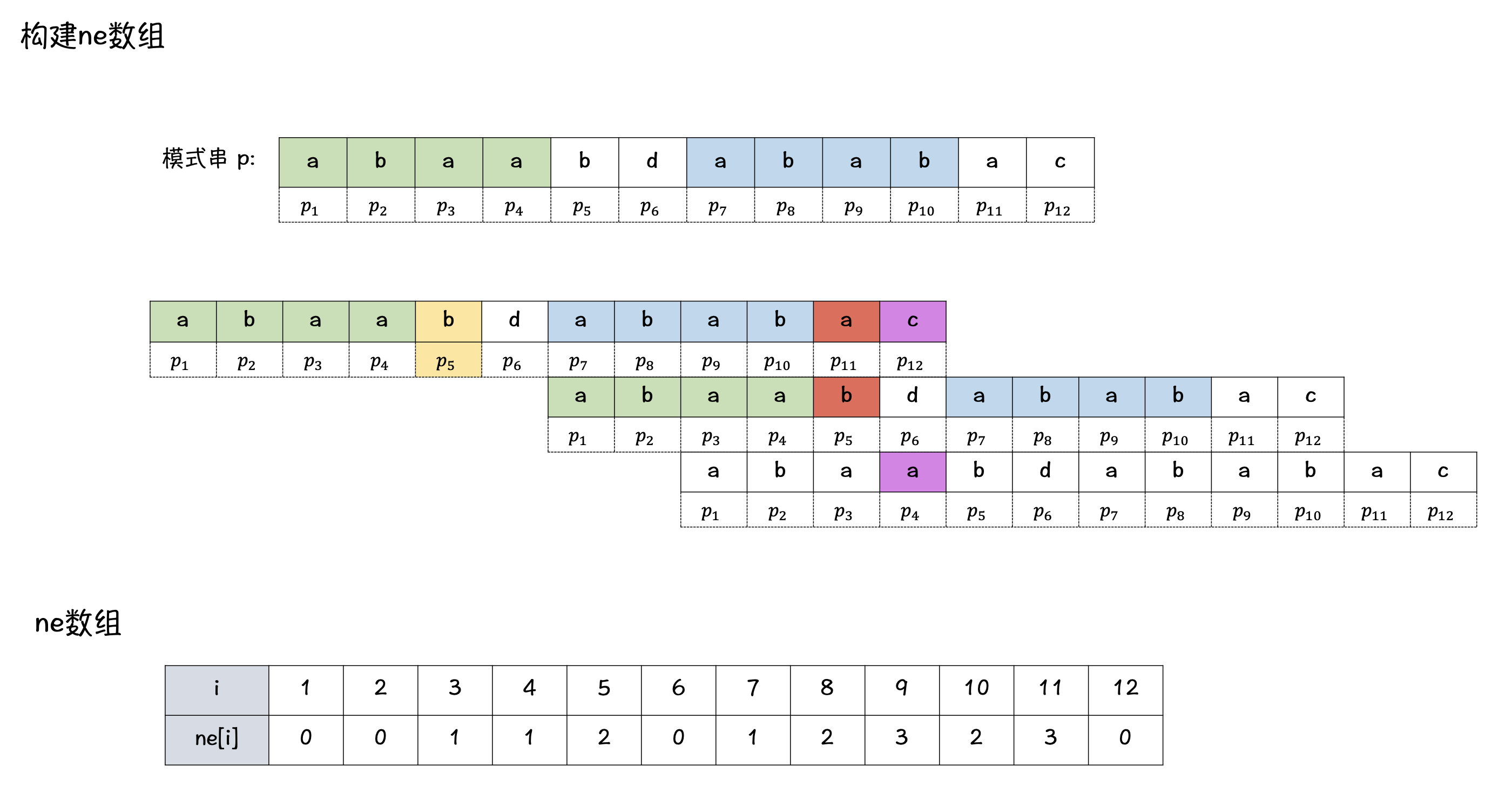
\(ne\) 数组的构建
当 \(j = 1\) 时,\(ne[1] = 0\),表示:前 \(1\) 个字符匹配失败,则重新开始匹配;
当 \(j > 1\) 时,\(ne[j] = k\),表示,前 \(j\) 个字符中,前缀 与 后缀 匹配的字符 最大长度 为 \(k\)
即:\(p_1\ p_2 \ \dots \ p_{k - 1} = p_{j-(k - 1)}\ p_{j-(k-2)}\ \dots \ p_{j-1}\)此时,若 \(p_k = p_j\),
则等式可以拓展为:\(p_1\ p_2 \ \dots \ p_{k - 1} \ p_k = p_{j-(k - 1)}\ p_{j-(k-2)}\ \dots \ p_{j-1} \ p_j\)
每次不断进行迭代,直到使等式延长的条件不满足,即出现: \(p_k \neq p_j\),
递推式为:$ne[j + 1]= ne[j] + 1 = k + 1 $
- 模式串 \(p\) 中第 \(ne[k]\) 的字符与 主串(这里也可以是 模式串 自身)中的第 \(j\) 个字符相比较。
令 \(ne[k] = t\),则有 \(p_t = p_j\)
说明此时在模式串中第 \(j+1\) 个字符之前存在一个长度为 \(t\) 的最长成功的部分,这段长度与从模式串中从首字母起,长度为 \(t\) 的子串相等。
即:\(p_1\ p_2 \ \dots \ p_t = p_{j-(t - 1)}\ p_{j-(t-2)}\ \dots \ p_j\)
得:$ne[j + 1]= ne[ne[j]] + 1 = t + 1 $
- 若 \(p_t \neq p_j\) ,那么模式串继续向右滑动,使得模式串第 \(ne[t]\) (也就是 \(ne[ne[k]]\))个字符与 \(p_j\) 对齐,如此反复。 会有两种情况:
- 直到 \(p_j\) 和模式串某个字符匹配成功。
- 不存在任何一个 \(t\) 满足:$$p_1\ p_2\ \dots \ p_t = p_{j−(t−1)}\ p_{j−(t−2)} \ \dots \ p_j \ \ \ (1 < t < k < j)$$ 则 \(ne[k + 1] = 0\)
时间复杂度:\(O(m + n)\)
示例(Example)

代码(Code)
-
构建 \(ne\) 数组:
for (int i = 2, j = 0; i <= n; i ++ ) { // 从 2 开始,位置 1 必然是 0 while (j && p[i] != p[j + 1]) j = ne[j]; if (p[i] == p[j + 1]) j ++ ; ne[i] = j; }
-
\(KMP\) 匹配:
for (int i = 1, j = 0; i <= n; i ++ ) { // 从 1 开始匹配主串 while (j && s[i] != p[j + 1]) j = ne[j]; if (s[i] == p[j + 1]) j ++ ; if (j == n) { cout << i - n << " "; j = ne[j]; // 可以不加 } }
应用(Application)
KMP字符串
给定一个字符串 \(S\),以及一个模式串 \(P\),所有字符串中只包含大小写英文字母以及阿拉伯数字。
模式串 \(P\) 在字符串 \(S\) 中多次作为子串出现。
求出模式串 \(P\) 在字符串 \(S\) 中所有出现的位置的起始下标。
输入格式
第一行输入整数 \(N\),表示字符串 \(P\) 的长度。
第二行输入字符串 \(P\)。
第三行输入整数 \(M\),表示字符串 \(S\) 的长度。
第四行输入字符串 \(S\)。
输出格式
共一行,输出所有出现位置的起始下标(下标从 \(0\) 开始计数),整数之间用空格隔开。
数据范围
\(1 \le N \le 10^5\)
\(1 \le M \le 10^6\)
输入样例:
3
aba
5
ababa
输出样例:
0 2
- 题解:
#include <cstdio> #include <iostream> #include <cstring> #include <ctime> #include <cmath> #include <map> #include <set> #include <unordered_set> #include <unordered_map> #include <sstream> #include <algorithm> #include <bitset> #include <vector> #include <deque> #define pb push_back #define opb pop_back #define yes puts("YES") #define no puts("NO") #define all(a) a.begin(), a.end() #define show(x) cout << x << '\n' #define rep2(i, a, b) for (int i = a; i <= b; i ++ ) #define rep1(i, a, b) for (int i = a; i < b; i ++ ) #define per2(i, a, b) for (int i = a; i >= b; i -- ) #define per1(i, a, b) for (int i = a; i > b; i -- ) #define fio ios::sync_with_stdio(false), cout.tie(0), cin.tie(0) #define ff first #define ss second using namespace std; typedef unsigned long long ull; typedef pair<int, int> pii; typedef pair<string, int> psi; typedef pair<double, double> pdd; typedef long long ll; const int N = 100010, M = N * 10; const int mod = 1000000007; const int inf = 0x3f3f3f3f; int n, m; char p[N], s[M]; int ne[N]; int main() { fio; cin >> n >> p + 1; cin >> m >> s + 1; for (int i = 2, j = 0; i <= n; i ++ ) { while (j && p[i] != p[j + 1]) j = ne[j]; if (p[i] == p[j + 1]) j ++ ; ne[i] = j; } for (int i = 1, j = 0; i <= m; i ++ ) { while (j && s[i] != p[j + 1]) j = ne[j]; if (s[i] == p[j + 1]) j ++ ; if (j == n) { cout << i - n << ' '; j = ne[j]; } } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号