哈希表(Hash Table)
简介(Introduction)
散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
描述(Description)
- 作用:把大的数据集合映射到一个小的空间(通过 \(hash\) 函数)如:将 \(0\sim 10^5\) 区间离散的数映射到 \(0\sim 10^3\) 范围内,只需把数 \(mod \ 10^3\)
Tip:由于值域的缩小,很有可能出现一个问题:两个数映射为一个数。
如: \(3 \ mod \ 2 = 1,\ \ 6 \ mod \ 2 = 1\)
- 离散化是特殊的哈希
- 模拟散列表基本操作:
- 插入一个数
- 查询一个数是否在集合中出现
- 方法:
- 开放寻址法:采用一个数组来存储,开辟数组约为数据范围的 \(2\sim 3\) 倍(质数) —— 负载因子
负载因子:已有节点数量 / 哈希表的大小(一般控制在 \(0.5 \sim 0.6\))
- 拉链法:
- 采用 单链表 来存储取 \(mod\) 后值相等的数的集合。
- \(mod\) 值尽可能取为 质数,且要尽可能远离 \(2\) 的整次幂,其可以使重复的 \(hash\) 值尽可能少
时间复杂度:\(O(1)\)
示例(Example)
- 拉链法:
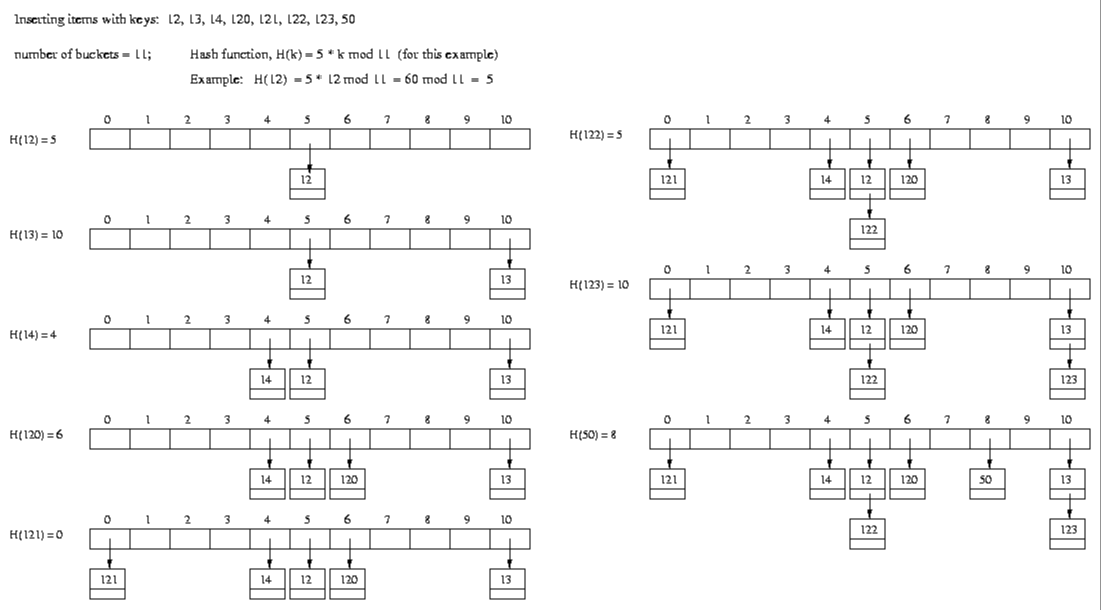
- 开放寻址法:
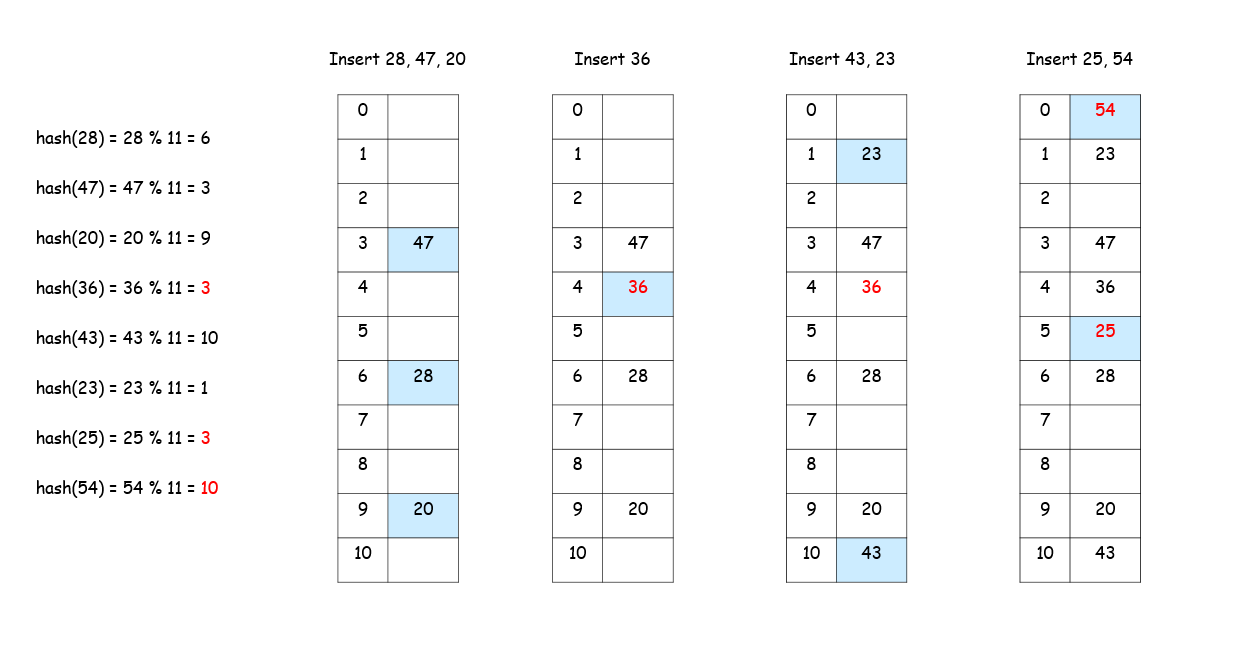
代码(Code)
-
开放寻址法:
const int N = 2e5 + 3; const int null = 0x3f3f3f3f; // 定义正无穷,表示不存在目标数。(要用这个值初始数组memset(h,0x3f,sizeof h)); int h[N]; int find(int x) { int k = (x % N + N) % N; while (h[k] != null && h[k] != x) // 说明当前位置有值,但是不是目标值。 k = (k + 1) % N; // 这个过程一定会停止,因为总共的空位比总的数的个数多。 return k; // 返回值为:1.插入位置 2.查找到x的对应位置 }
-
拉链法:一个数组下面的每个元素挂有链表
const int N = 1e5 + 3; int h[N], e[N], ne[N], idx; void insert(int x) { int k = (x % N + N) % N; // 要把负数也映射为正数。(c++ 中负数 mod 一个正数还是负数。) e[idx] = x, ne[idx] = h[k], h[k] = idx ++ ; // 链表头插 } bool find(int x) { int k = (x % N + N) % N; for(int i = h[k]; ~i; i = ne[i]) // 链表查询遍历 if(e[i] == x) return true; return false; }
应用(Application)
模拟散列表
维护一个集合,支持如下几种操作:
I x,插入一个数x;Q x,询问数x是否在集合中出现过;现在要进行
N次操作,对于每个询问操作输出对应的结果。输入格式
第一行包含整数
N,表示操作数量。接下来
N行,每行包含一个操作指令,操作指令为I x,Q x中的一种。输出格式
对于每个询问指令
Q x,输出一个询问结果,如果x在集合中出现过,则输出Yes,否则输出No。每个结果占一行。
数据范围
1 ≤ N ≤ 105
−109 ≤ x ≤109
输入样例:
5
I 1
I 2
I 3
Q 2
Q 5
输出样例:
Yes
No
-
题解:
// C++ Version // 开放寻址法 #include <cstring> #include <iostream> using namespace std; const int N = 2e5 + 3; const int null = 0x3f3f3f3f; int h[N]; int find(int x) { int k = (x % N + N) % N; while (h[k] != null && h[k] != x) k = (k + 1) % N;。 return k; } int main() { int n; scanf("%d", &n); memset(h, 0x3f, sizeof h); while (n -- ) { char op[2]; int x; scanf("%s%d", op, &x); if (op[0] == 'I') h[find(x)] = x; else { if (h[find(x)] == null) puts("No"); else puts("Yes"); } } return 0; }// C++ Version // 拉链法 —— 一个数组下面的每个元素挂有链表 #include <cstring> #include <iostream> using namespace std; const int N = 1e5 + 3; int n; int h[N], e[N], ne[N], idx; bool find(int x) { int k = (x % N + N) % N; for (int i = h[k]; ~i; i = ne[i]) if (e[i] == x) return true; return false; } void add(int a, int b) { e[idx] = x, ne[idx] = h[k], h[k] = idx ++ ; } void insert(int x) { int k = (x % N + N) % N; if (find(x)) return; add(k, x); } int main() { scanf("%d", &n); memset(h, -1, sizeof h); while (n -- ) { char op[2]; int x; scanf("%s%d", op, &x); if(op[0] == 'I') insert(x); else { if(!find(x)) puts("No"); else puts("Yes"); } } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号