B树和B+树
简介(Introduction)
在计算机科学中,\(B\) 树(B-tree) 是一种自平衡的树,能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作,都在对数时间内完成。\(B\) 树,概括来说是一个一般化的二叉查找树,可以拥有多于 \(2\) 个子节点。与自平衡二叉查找树不同,\(B\) 树为系统大块数据的读写操作做了优化。\(B\) 树减少定位记录时所经历的中间过程,从而加快存取速度。\(B\) 树这种数据结构可以用来描述外部存储。这种数据结构常被应用在 数据库 和 文件系统 的实现上。
描述(Description)
- \(B\) 树性质:
- \(m\) 阶 \(B\) 树,每个节点 最多 有 \(m\) 个孩子。
- 每个节点最多有 \(m-1\) 个关键字(可以存有的键值对)。
- 根节点最少可以只有 \(1\) 个关键字。
- 非根节点至少有 \(\large {\lceil m / 2\rceil} -1\) 个关键字。
- 每个节点中的关键字都按照 从小到大 的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。
- 所有叶节点都位于同一层,或者说根节点到每个叶节点的长度都相同。
- 每个节点都存有索引和数据,也就是对应的 \(key\) 和 \(value\)。
- 所以,根节点的关键字数量范围:\(1 \le k \le m-1\),非根节点的关键字数量范围:\(\large {\lceil m / 2\rceil} - 1 \le k \le m-1\)。
- \(B\) 树插入:
- 如果 \(B\) 树中已存在需要插入的键值对,则用需要插入的值替换旧的值,若 \(B\) 树不存在这个 \(key\),则一定是在叶结点中进行插入操作。
- 根据要插入的 \(key\) 的值,找到叶结点并插入。
- 判断当前结点 \(key\) 的个数是否 $ \le m-1$,若满足则结束,否则进行第 \(3\) 步。
- 以结点中间的 \(key\) 为中心分裂成左右两部分,然后将这个中间的 \(key\) 插入到父结点中,\(key\) 的左子树指向分裂后的左半部分,\(key\) 的右子支指向分裂后的右半部分,然后将当前结点指向父结点,继续进行第 \(3\) 步。
- \(B\) 树删除:
- 如果不存对应 \(key\),则删除失败。
- 如果当前需要删除的 \(key\) 位于非叶结点上,则用后继 \(key\) 覆盖待删除的 \(key\) ,然后在后继 \(key\) 所在的子支中删除该后继 \(key\) 。此时后继 \(key\) 一定位于叶结点上,删除这个记录后执行第 \(2\) 步
- 该结点 \(key\) 个数 \(\ge \lceil {\large \frac m 2} \rceil - 1\),结束删除操作,否则执行第 \(3\) 步。
- 如果兄弟结点 \(key\) 个数 \(> \lceil {\large \frac m 2} \rceil - 1\),则父结点中的 \(key\) 下移到该结点,兄弟结点中的一个 \(key\) 上移,删除操作结束 —— 从隔壁借
否则,将父结点中的 \(key\) 下移与当前结点及它的兄弟结点中的 \(key\) 合并,形成一个新的结点。原父结点中的 \(key\) 的两个元素就变成了一个元素,指向这个新结点。然后当前结点的指针指向父结点,重复上第 \(2\) 步。
Tips:有些结点它可能即有左兄弟,又有右兄弟,那么任意选择一个兄弟结点进行操作即可。
- \(B+\) 树性质:
- \(B+\) 树中,每个关键字对应一颗子树,即:具有 \(n\) 个关键字的节点含有 \(n\) 棵子树,\(B\) 树中 \(n\) 个关键字的节点含有 \(n + 1\) 棵子树
- \(B+\) 树中,每个节点(非根)的关键字个数 \(n\) 的范围是:\(\lceil m / 2 \rceil \le n \le m\)(根节点:\(1\le n\le m\));\(B\) 树中,每个节点(非根)的关键字个数 \(n\) 的范围是:\(\lceil m / 2 \rceil - 1 \le n \le m - 1\)(根节点:\(1\le n\le m - 1\))
- \(B+\) 树跟 \(B\) 树不同 \(B+\) 树的非叶节点不保存关键字记录的指针,只进行数据索引,这样使得 \(B+\) 树每个非叶节点所能保存的关键字大大增加
- \(B+\) 树叶节点保存了父节点的所有关键字记录的指针,所有数据地址必须要到叶节点才能获取到,所以每次数据查询的次数都一样
- \(B+\) 树叶节点的关键字从小到大有序排列,左边结尾数据都会保存右边节点开始数据的指针
-
\(B+\) 树插入:
- 若为空树,创建一个叶结点,然后将记录插入其中,此时这个叶结点也是根结点,插入操作结束。
- 对于叶结点:根据 \(key\) 值找到叶结点,向这个叶结点插入记录。插入后,若当前结点 \(key\) 的个数 \(\le m-1\),则插入结束。否则将这个叶结点分裂成左右两个叶结点,左叶结点包含前 \(\large \frac m 2\) 个记录,右结点包含剩下的记录,将第 \({\large \frac m 2} + 1\) 个记录的 \(key\) 进位到父结点中(父结点一定是索引类型结点),进位到父结点的 \(key\) 左孩子指针向左结点,右孩子指针向右结点。将当前结点的指针指向父结点,然后执行第 \(3\) 步。
- 对于非叶结点:若当前结点 \(key\) 的个数 \(\le m-1\),则插入结束。否则,将这个索引类型结点分裂成两个索引结点,左索引结点包含前 \(\large \frac {m-1} 2\) 个 \(key\),右结点包含 \(m- \large \frac m 2\)个 \(key\),将第 \(\large \frac m 2\) 个 \(key\) 进位到父结点中,进位到父结点的 \(key\) 左孩子指向左结点, 进位到父结点的 \(key\) 右孩子指向右结点。将当前结点的指针指向父结点,然后重复第 \(3\) 步。
-
\(B+\) 树删除:
- 如果叶结点中没有相应的 \(key\),则删除失败。否则执行下面的步骤
- 删除叶子结点中对应的 \(key\) 。删除后若结点的 \(key\) 的个数 $\ge \lceil {\large \frac {m - 1} 2} \rceil -1 $,删除操作结束,否则执行第 \(2\) 步。
- 若兄弟结点 \(key\) 有富余 \((> \lceil {\large \frac {m - 1} 2} \rceil -1)\),向兄弟结点借一个记录,同时用借到的 \(key\) 替换父结(指当前结点和兄弟结点共同的父结点)点中的 \(key\) ,删除结束。否则执行第 \(3\) 步。
- 若兄弟结点中没有富余的 \(key\) ,则当前结点和兄弟结点合并成一个新的叶子结点,并删除父结点中的 \(key\) (父结点中的这个 \(key\) 两边的孩子指针就变成了一个指针,正好指向这个新的叶子结点),将当前结点指向父结点(必为索引结点),执行第 \(4\) 步(第 \(4\) 步以后的操作和B树就完全一样了,主要是为了更新索引结点)。
- 若索引结点的 \(key\) 的个数 $\ge \lceil {\large \frac {m - 1} 2} \rceil -1 $,则删除操作结束。否则执行第 \(5\) 步
- 若兄弟结点有富余,父结点 \(key\) 下移,兄弟结点 \(key\) 上移,删除结束。否则执行第 \(6\) 步
- 当前结点和兄弟结点及父结点下移 \(key\) 合并成一个新的结点。将当前结点指向父结点,重复第 \(4\) 步。
Tip: 通过 \(B+\) 树的删除操作后,索引结点中存在的 \(key\),不一定在叶子结点中存在对应的记录。
示例(Example)
- 插入:
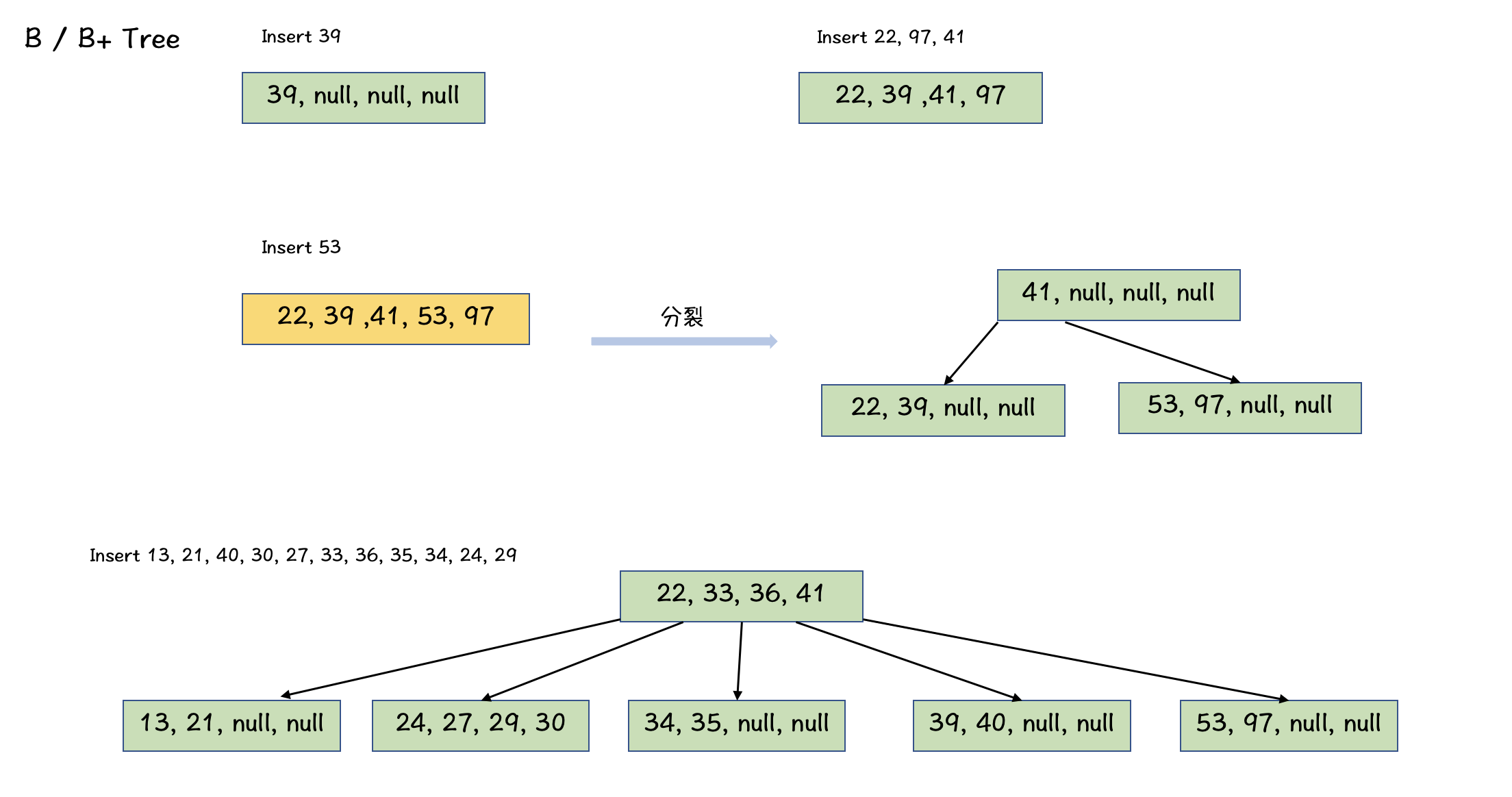
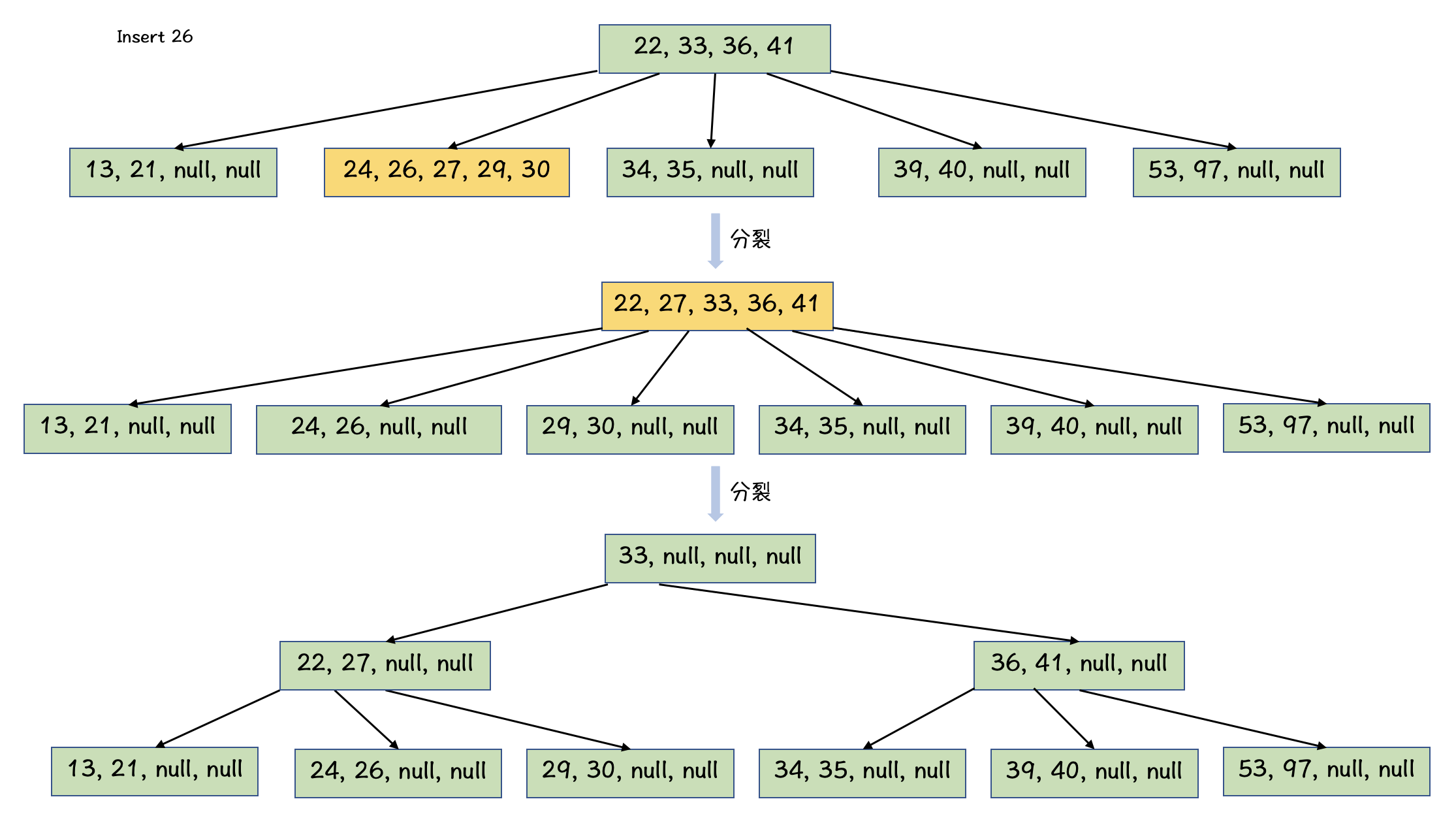

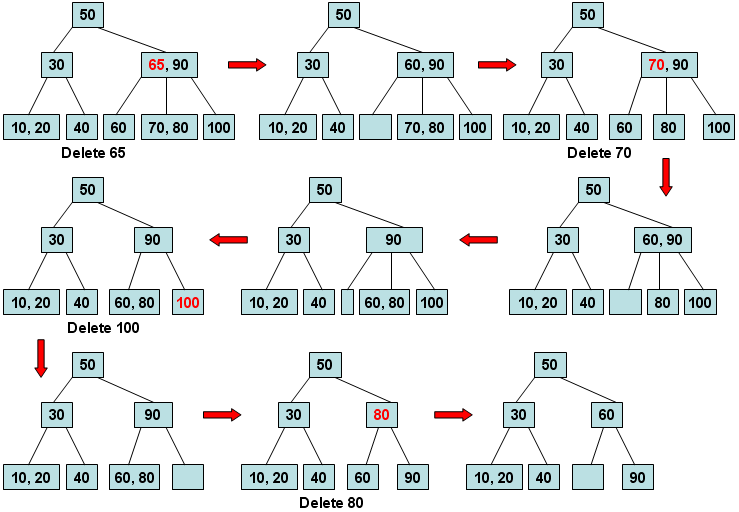

 浙公网安备 33010602011771号
浙公网安备 33010602011771号