查找
简介(Introduction)
在计算机科学中定义为:在一些(有序的/无序的)数据元素中,通过一定的方法找出与给定关键字相同的数据元素的过程叫做查找。也就是根据给定的某个值,在查找表中确定一个关键字等于给定值的记录或数据元素。
描述(Description)
- \(ASL\)(Average Search Length),即平均查找长度,定义为:
平均查找长度 \(ASL\) = 每个元素的查找概率 \(*\) 找到第 \(i\) 个元素需要进行的比较次数的和。
即,
$$ASL = \sum_{i = 1}^np_ic_i$$
其中 \(n\) 为查找表中元素的个数,一般情况下,每个元素被找到的概率相同, 即 \(p_i = \frac 1 n\),\(c_i\) 是查找到第 \(i\) 个元素比较的次数。
- 一个查找算法中,\(ASL\) 的值越大,说明该性能越差,反之,性能越好
- 每个判断都对应一个 决策树
- 顺序查找 (Sequence Search)
- 从头扫到尾,找到待查找元素即查找成功,若到尾部没有找到,说明查找失败。
- 一般线性表:
- 查找成功:$$ASL_{成功} = \sum_{i = 1} ^m p_ic_i = \frac {1}{n} \sum_{i = 1} ^n i = \frac 1 n * \frac {n(n - 1)}{2} = \frac {n + 1} 2 $$
- 查找失败:$$ASL_{失败} = n$$
- 有序线性表:
- 查找成功:$$ASL_{成功} = \sum_{i = 1} ^m p_ic_i = \frac {1}{n} \sum_{i = 1} ^n i = \frac 1 n * \frac {n(n - 1)}{2} = \frac {n + 1} 2 $$
- 查找失败:$$ASL_{失败} = \frac{\sum_{i = 1}^n i + n}{n + 1} = \frac{n}{2} + \frac{n}{n + 1}$$
- 从头扫到尾,找到待查找元素即查找成功,若到尾部没有找到,说明查找失败。
- 折半查找 (Binary Search)
- 条件:待查找表是 有序 表
- 在折半查找中,用 二叉树 描述查找过程,查找区间中间位置作为根,左子表为左子树,右子表为右子树
- 若查找元素为 \(k\),先与树根结点进行比较,若 \(k\) 小于根,则转向左子树继续比较,若 \(k\) 大于根,则转向右子树,递归上述过程,直到查找成功或查找失败。
\[ASL_{成功} = ASL_{失败} = \sum_{i = 1} ^ n l_i = \frac{1}{n} (1 * 1 + 2 * 2 + \dots + h * 2^{h - 1}) = \frac{n + 1}{n} \log_2{(n + 1)} - 1 \approx log_2 (n + 1) - 1 \]
- 分块查找 (Block Search)
- 分块查找又称 索引顺序查询,即:块间使用 折半查找,块内使用 顺序查找
- 一般默认:块内无序,块间有序
- 设共有 \(n\) 个元素,每块有 \(s\) 个元素,则共有 \(b = n / s\) 块。
设查找到对应块的 \(ASL\) 为:\(L_l\),块中查找对应元素的 \(ASL\) 为:\(L_s\),则平均查找长度为 $$ASL = L_l+L_s=\frac{b + 1} 2 + \frac{s + 1}{2} = \frac{s^2 + 2s + n}{2s}$$
当 \(s = \sqrt n\) 时,\(ASL\) 取得最小值 \(ASL_{min} = \sqrt n + 1\)
示例(Example)
-
顺序查找
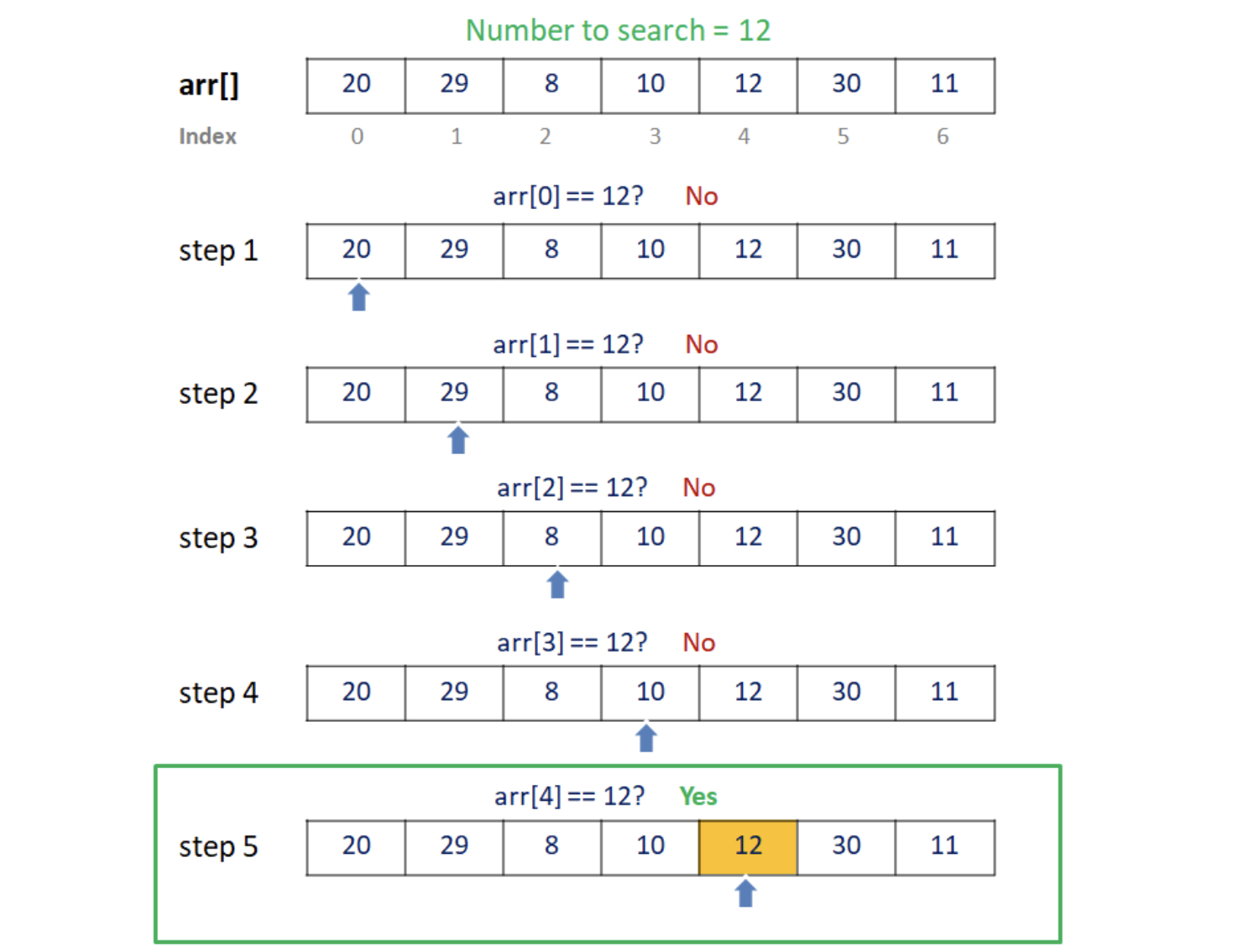
-
折半查找
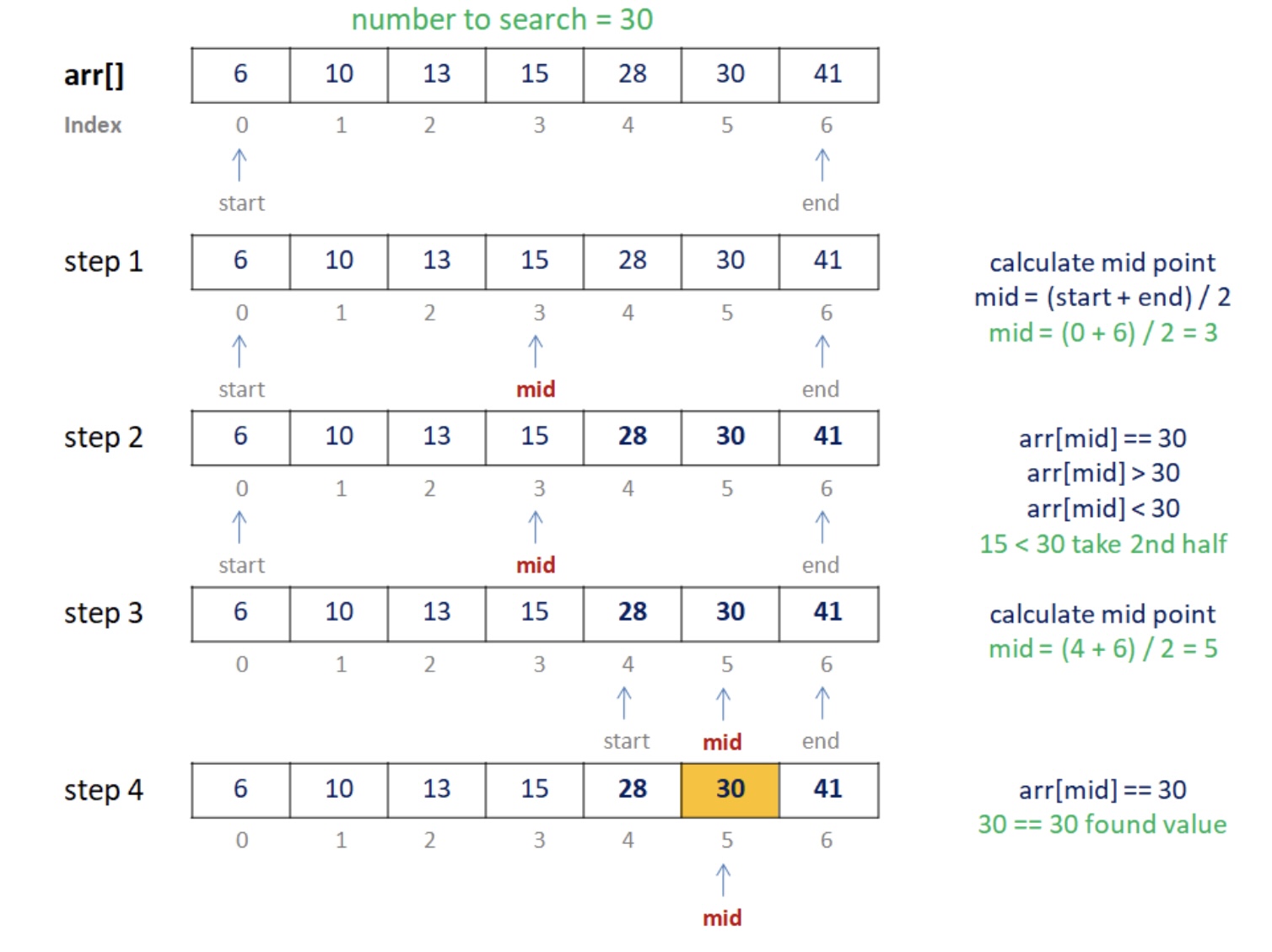
-
分块查找
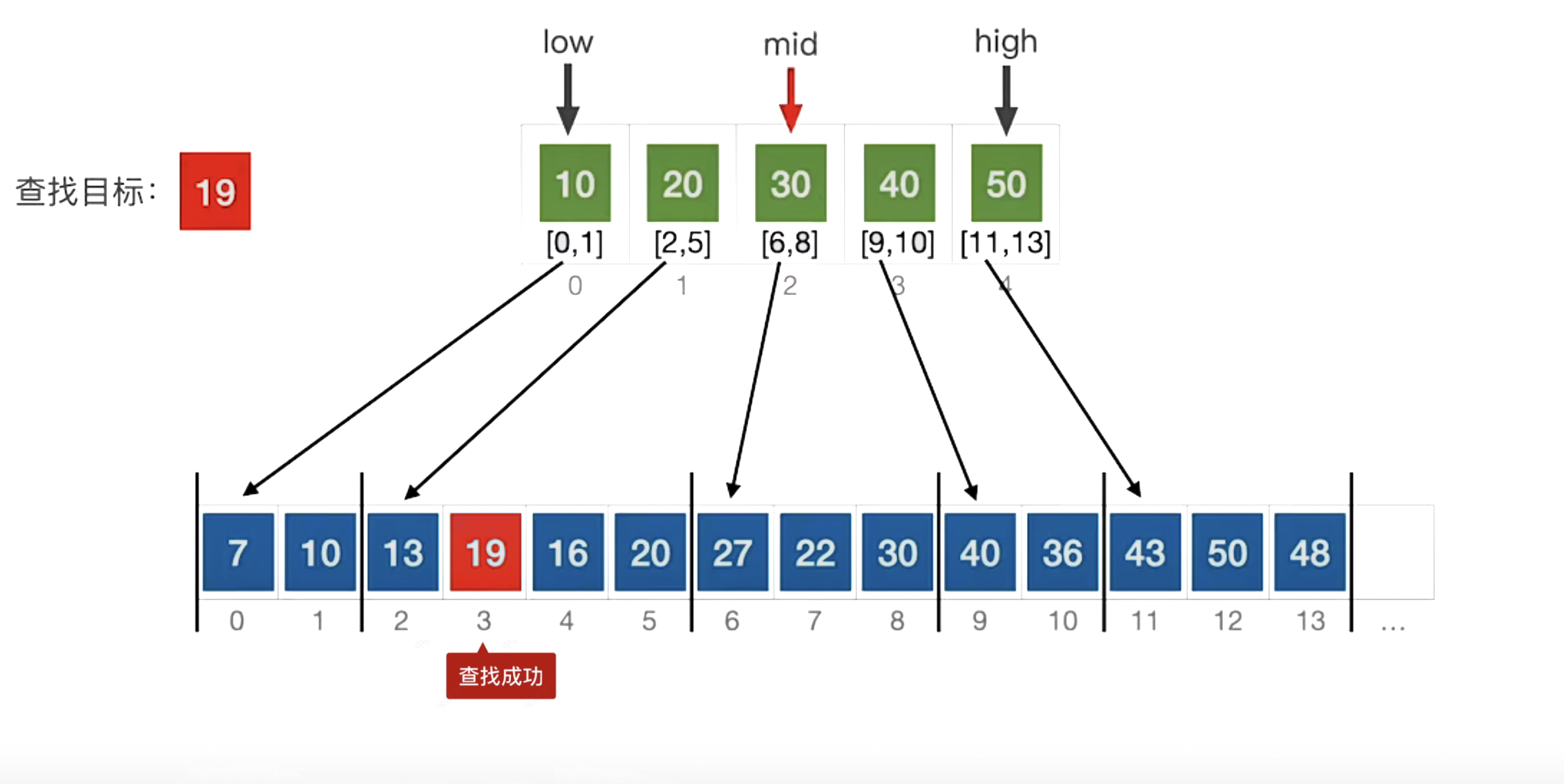
代码(Code)
- 折半查找:
int binary_search(int arr[], int n, int key) { int l = 0, r = n - 1; while (l <= r) { int mid = l + r >> 1; if (arr[mid] == key) return mid; else if (arr[mid] > key) r = mid - 1; else l = mid + 1; } return -1; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号