关键路径
简介(Introduction)
关键路径 是指设计中从输入到输出经过的延时最长的逻辑路径。优化关键路径是一种提高设计工作速度的有效方法。
一般地,从输入到输出的延时取决于信号所经过的延时最大路径,而与其他延时小的路径无关。在优化设计过程中关键路径法可以反复使用,直到不可能减少关键路径延时为止。
描述(Description)
-
概念:
- \(AOE\) 网:
- 用顶点表示事件,弧表示活动,弧上的权值表示活动持续的时间的有向图叫 \(AOE\)(Activity On Edge)网。在建筑学中也称为关键路线。\(AOE\) 网常用于估算工程完成时间。
- \(AOE\) 网的性质:(\(DAG\) 性质)
- 只有在某个顶点所代表的事件发生后,从该点出发的各有向边所代表的活动才能开始
- 只有在进入某顶点的各有向边所代表的活动都已结束,该顶点所代表的事件才能发生
- 开始顶点 (源点):\(AOE\) 网中,唯一一个入度为 \(0\) 的顶点
- 结束顶点 (汇点):\(AOE\) 网中,唯一一个出度为 \(0\) 的顶点
- 关键路径:该图中的最长路
- 关键活动:关键路径上的活动
- \(AOE\) 网:
Tips:
- 事件:代表点(状态),活动:代表边(过程)
- 从 源点 到 汇点 的有向路径可能有 多条
- 常用参量:
-
事件 \(v_k\) 的最早发生时间 \(ve(k)\) —— 从前向后取最大
- 决定了所有从 \(v_k\) 开始的活动能够开工的最早时间
-
事件 \(v_k\) 的最迟发生时间 \(vl(k)\) —— 从后向前取最小
- 指在不推迟整个工程完成的前提下,该事件最迟必须发生的时问
-
活动 \(a_i\) 的最早开始时间 \(e(i)\)
- 指该活动弧的起点所表示的事件的最早发生时间
-
活动 \(a_i\) 的最迟开始时间 \(l(i)\)
- 指该活动弧的终点所表示事件的最迟发生时间与该活动所需时间之差
-
活动 \(a_i\) 的 时间余量 \(d(i) = l(i)-e(i)\),表示在不增加完成整个工程所需总时间的情况下,活动 \(a_i\) 可以拖延的时间,若一个活动的 时间余量为零,则说明该活动 必须 要如期完成。
-
- 步骤:
- 求所有 事件 的 最早 发生时间 \(ve()\)
- 求所有 事件 的 最迟 发生时间 \(vl()\)
- 求所有 活动 的 最早 发生时间 \(e()\)
- 求所有 活动 的 最迟 发生时间 \(l()\)
- 求所有活动的 时间余量 \(d()\)
注:\(d(i)=0\),即 \(l(i)=e(i)\) 的活动 \(a_i\) 是 关键活动,由关键活动组成的路径就是 关键路径。
示例(Example)
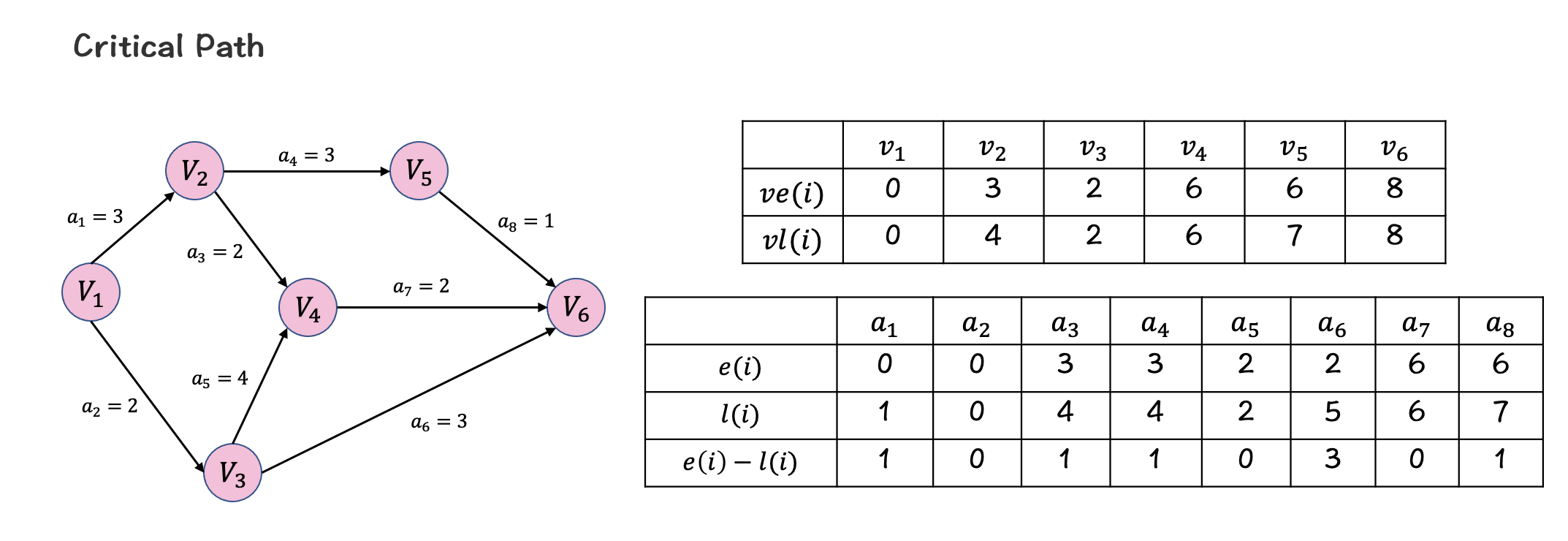 '
'


 浙公网安备 33010602011771号
浙公网安备 33010602011771号