Kruskal Algorithm
简介(Introduction)
克鲁斯卡尔算法\((Kruskal)\) 是求连通网的最小生成树的另一种方法。
\(Kruskal\) 算法是一种常见并且好写的最小生成树算法。
描述(Description)
- \(Kruskal\) 算法流程:
- 建立并查集,每个节点各自构成一个集合。
- 先将所有边按权值从小到大排序。
- 依次扫描每条边 \((x,y,w)\),若 \(x, y\) 属于同一集合(连通),则忽略该边,继续扫描下一条边。
- 否则,合并 \(x, y\) 所在的集合,并把 \(w\) 累加到答案中。
- 所有边扫描完成后,步骤 \(4\) 中处理过的边就构成了 最小生成树。
时间复杂度:\(O(mlogm)\)
示例(Example)
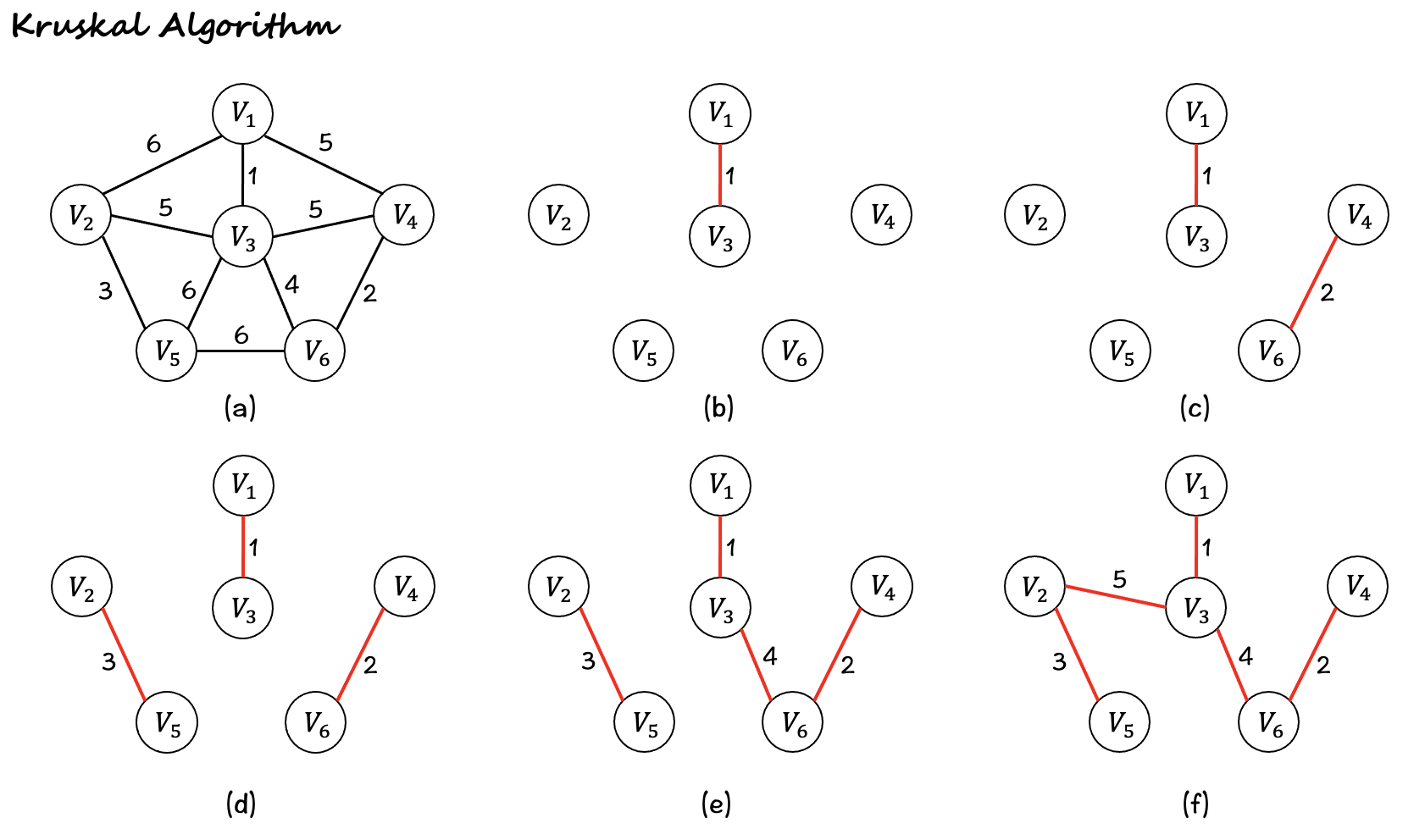
- 运行结果:

代码(Code)
- 并查集:
int find(int x) { return (fa[x] == x) ? x : fa[x] = find(fa[x]); }
- 结构体:
struct Edge{ int a, b, w; bool operator <(const Edge &t) const { // 重载 < , 按边的权值进行排序 return w < t.w; } } edges[100010];
- \(Kruskal\) 算法:
// C++ Version int kruskal() { for (int i = 1; i <= n; i ++ ) fa[i] = i; sort(edge, edge + m); int res = 0, cnt = 0; for (int i = 0; i < m; i ++ ) { int a = edge[i].a, b = edge[i].b, w = edge[i].w; a = find(a), b = find(b); if (a != b) { cnt ++ ; res += w; fa[a] = b; } } if (cnt < n - 1) return inf; return res; }
应用(Application)
口袋的天空
小杉坐在教室里,透过口袋一样的窗户看口袋一样的天空。
有很多云飘在那里,看起来很漂亮,小杉想摘下那样美的几朵云,做成棉花糖。
题目描述
给你云朵的个数 \(N\),再给你 \(M\) 个关系,表示哪些云朵可以连在一起。
现在小杉要把所有云朵连成 \(K\) 个棉花糖,一个棉花糖最少要用掉一朵云,小杉想知道他怎么连,花费的代价最小。
输入格式
第一行有三个数 \(N,M,K\)。
接下来 \(M\) 行每行三个数 \(X,Y,L\),表示 \(X\) 云和 \(Y\) 云可以通过 \(L\) 的代价连在一起。
输出格式
对每组数据输出一行,仅有一个整数,表示最小的代价。
如果怎么连都连不出 \(K\) 个棉花糖,请输出
No Answer。数据范围:
对于 \(30\%\) 的数据,\(1 \le N \le 100\),\(1\le M \le 10^3\);
对于 \(100\%\) 的数据,\(1 \le N \le 10^3\),\(1 \le M \le 10^4\),\(1 \le K \le 10\),\(1 \le X,Y \le N\),\(0 \le L<10^4\)。
输入样例:
3 1 2
1 2 1
输出样例:
1
- 题解:
// C++ Version #include <cstdio> #include <iostream> #include <cstring> #include <ctime> #include <cmath> #include <map> #include <set> #include <unordered_set> #include <unordered_map> #include <sstream> #include <algorithm> #include <bitset> #include <vector> #include <deque> #define pb push_back #define opb pop_back #define yes puts("YES") #define no puts("NO") #define all(a) a.begin(), a.end() #define show(x) cout << x << '\n' #define rep1(i, a, b) for (int i = a; i < b; i ++ ) #define rep2(i, a, b) for (int i = a; i <= b; i ++ ) #define per1(i, a, b) for (int i = a; i > b; i -- ) #define per2(i, a, b) for (int i = a; i >= b; i -- ) #define fio ios::sync_with_stdio(false), cout.tie(0), cin.tie(0) #define ff first #define ss second using namespace std; typedef unsigned long long ull; typedef pair<int, int> pii; typedef pair<string, int> psi; typedef pair<double, double> pdd; typedef long long ll; const int N = 100010, M = 510; const int mod = 1000000007; const int inf = 0x3f3f3f3f; int n, m, k; int fa[N]; struct Edge { int x, y,z; bool operator < (const Edge & a) const { return z < a.z; } } edge[N]; int find(int p) {return fa[p] == p ? p : fa[p] = find(fa[p]);} int main() { fio; cin >> n >> m >> k; rep2 (i, 1, n) fa[i] = i; rep2 (i, 1, m) { int x, y, z; cin >> x >> y >> z; edge[i] = {x, y, z}; } if (k > n) { show("No Answer"); return 0; } sort(edge + 1, edge + 1 + m); int ans = 0, cnt = 0; rep2 (i, 1, m) { Edge t = edge[i]; if (find(t.x) != find(t.y)) { ans += t.z; fa[find(t.x)] = fa[find(t.y)]; cnt ++ ; } if (cnt == n - k) break; } if (cnt != n - k) show("No Answer"); else show(ans); return 0; }
补充(Supplement)
次小生成树:
定义:给一个带权的图,把图的所有生成树按权值从小到大排序,第二小的称为次小生成树。
求解:
- 方法一:先求最小生成树,再枚举删去最小生成树中的边求解。时间复杂度:\(O(mlogm + nm)\)
- 方法二:先求最小生成树,然后依次枚举非树边,然后将该边加入树中,同时从树中去掉一条边,使得最终的图仍是一棵树。则一定可以求出次小生成树。
步骤:
- 求出无向图的最小生成树 \(T\),设其权值和为 \(M\)
- 遍历每条未被选中的边 \(e = (u,v,w)\),找到 \(T\) 中 \(u\) 到 \(v\) 路径上边权最大的一条边 \(e' = (s,t,w')\),则在 \(T\) 中以 \(e\) 替换 \(e'\),可得一棵权值和为 \(M' = M + w - w'\) 的生成树 \(T'\).
- 对所有替换得到的答案 \(M'\) 取最小值即可


 浙公网安备 33010602011771号
浙公网安备 33010602011771号