Floyd Alogrithm

简介(Introduction)

Floyd算法 又称为 插点法，是一种利用 动态规划 的思想寻找给定的 加权图中多源点之间最短路径 的算法，与 \(Dijkstra\) 算法类似

描述(Description)

• \(Floyd\) 算法是一个用来处理 多源最短路的 算法
• 图是使用 邻接矩阵 来储存
• \(Floyd\) 算法求解的经典问题：
  1. 最短路问题
  2. 传递闭包问题
  3. 找最小环问题
  4. 恰好经过 \(k\) 条边的最短路问题（倍增）

时间复杂度为: \(O(n^3)\)

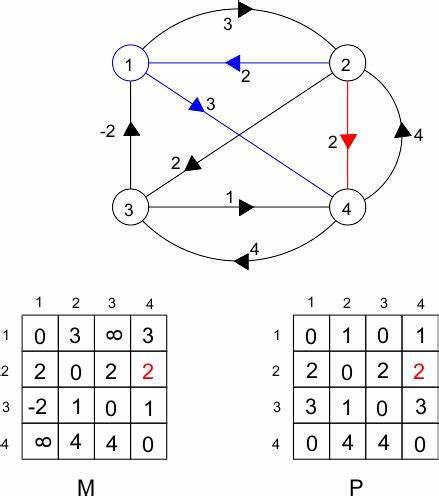
示例(Example)

代码(Code)

• 初始化：

  void init() {
  	for (int i = 1; i <= n; i ++ )
  		for (int j = 1; j <= n; j ++ )
  			if (i == j) d[i][j] = 0;
  			else d[i][j] = 0x3f3f3f3f;
  }
  

• \(Floyd\) 算法：

  void floyd() {
  	for (int k = 1; k <= n; k ++ )
  		  for (int i = 1; i <= n; i ++ )
  			  for (int j = 1; j <= n; j ++ )
  					 d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
  }
  

应用(Application)

---

Floyd 求最短路

---

给定一个 \(n\) 个点 \(m\) 条边的有向图，图中可能存在重边和自环，边权可能为负数。

再给定 \(k\) 个询问，每个询问包含两个整数 \(x\) 和 \(y\)，表示查询从点 \(x\) 到点 \(y\) 的最短距离，如果路径不存在，则输出 impossible。

数据保证图中不存在负权回路。

输入格式

第一行包含三个整数 \(n,m,k\)。

接下来 \(m\) 行，每行包含三个整数 \(x,y,z\)，表示存在一条从点 \(x\) 到点 \(y\) 的有向边，边长为 \(z\)。

接下来 \(k\) 行，每行包含两个整数 \(x,y\)，表示询问点 \(x\) 到点 \(y\) 的最短距离。

输出格式

共 \(k\) 行，每行输出一个整数，表示询问的结果，若询问两点间不存在路径，则输出 impossible。

数据范围

\(1 \le n \le 200\),

\(1 \le k \le n^2\)

\(1 \le m \le 20000\),

图中涉及边长绝对值均不超过 \(10000\)。

输入样例：

3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3

输出样例：

impossible
1

• 题解：

  // C++ Version
  
  #include <cstdio>
  #include <cstring>
  
  using namespace std;
  
  const int N = 210, INF = 1e9;
  
  int d[N][N];
  int n, m, k;
  
  void floyd() {
  	for (int k = 1; k <= n; k++)
  		for (int i = 1; i <= n; i++)
  			for (int j = 1; j <= n; j++)
  				d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
  }
  
  int main() {
  	scanf("%d%d%d", &n, &m, &k);
  
  	//初始化d
  	for (int i = 1; i <= n; i ++ )
  		for (int j = 1; j <= n; j ++ )
  			if (i == j) d[i][j] = 0; // 存在自环，初始化将自身赋值为0，最短路就是0
  			else d[i][j] = INF;
  
  	while (m -- ) {
  		int a, b, c;
  		scanf("%d%d%d", &a, &b, &c);
  		d[a][b] = min(d[a][b], c);  // 若有重边保存最小
  	}
  
  	floyd();
  
  	while (k -- ) {
  		int a, b;
  		scanf("%d%d", &a, &b);
  
  		// 因为存在负权边, 所以 0x3f3f3f3f 这个值可能会因为负值被更新 但值依然远大于 0x3f3f3f3f / 2
  		if (d[a][b] > INF / 2) puts("impossible"); 
  		else printf("%d\n", d[a][b]);
  	}
  	return 0;
  }
  

---