平衡树(Balance Tree)
简介(Introduction)
平衡树 (Balance Tree,BT) 指的是,任意节点的子树的高度差都 \(\le1\)。
常见的符合平衡树的有,B树(多路平衡搜索树)、AVL树(二叉平衡搜索树)等。
描述(Description)
- 平衡树是在维持 \(BST\) 性质的基础上,通过改变二叉查找树的形态,使得树上每个节点的左右子树达到 平衡,从而使树的 深度 维持在 \(O(\log n)\) 级别
-
从下往上(叶节点向根节点)看,当树的高度差 \(>1\) (不平衡)时,此时需要对该根节点进行 “旋转” 操作
-
基本操作:(详情请见示例)
- 右旋 \((zig)\): \(zig(p)\) 可以理解为把 \(p\) 的左子节点围绕着 \(p\) 向右旋转
- 左旋 \((zag)\): \(zag(p)\) 可以理解为把 \(p\) 的右子节点围绕着 \(p\) 向左旋转
- 四种旋转情况:
- 左左 \((LL)\):进行一次 右旋
- 右右 \((RR)\):进行一次 左旋
- 左右 \((LR)\):先进行一次 左旋,进行一次 右旋
- 右左 \((RL)\):先进行一次 右旋,进行一次 左旋
- 操作:
- 遍历二叉搜索树
- 查找最小/最大值
- 插入一个元素
- 删除一个元素
- 求元素的排名
- 查找排名为 \(k\) 的元素
示例(Example)
-
平衡树
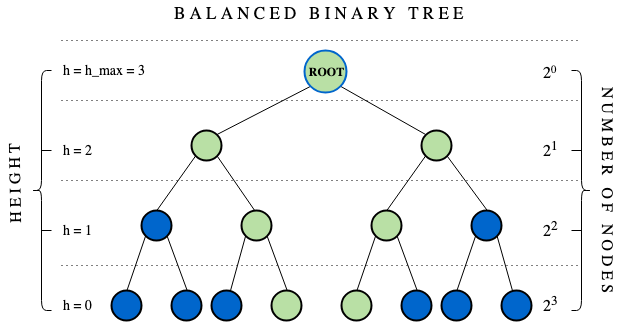
-
插入
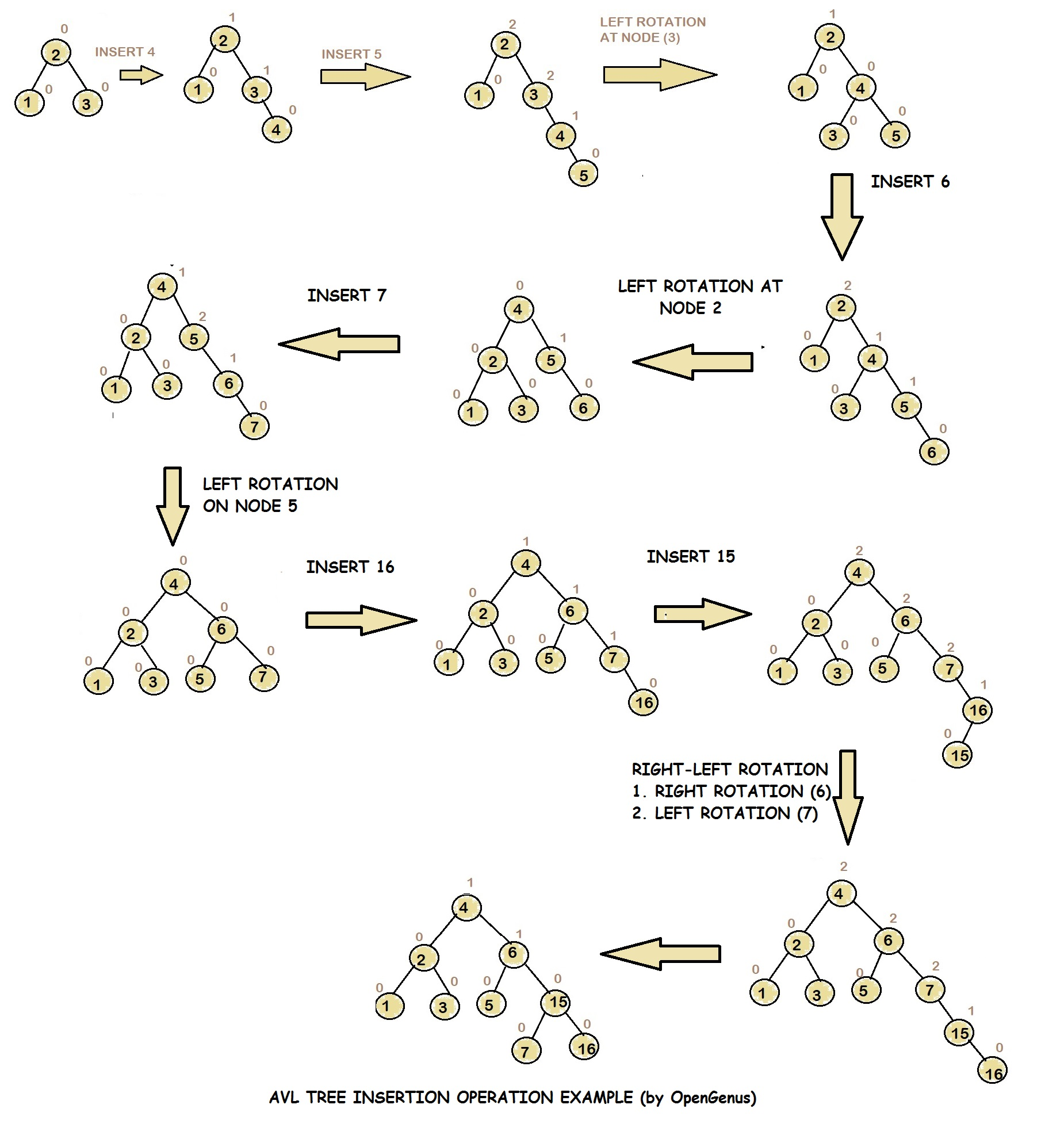
-
左旋 \(\&\) 右旋
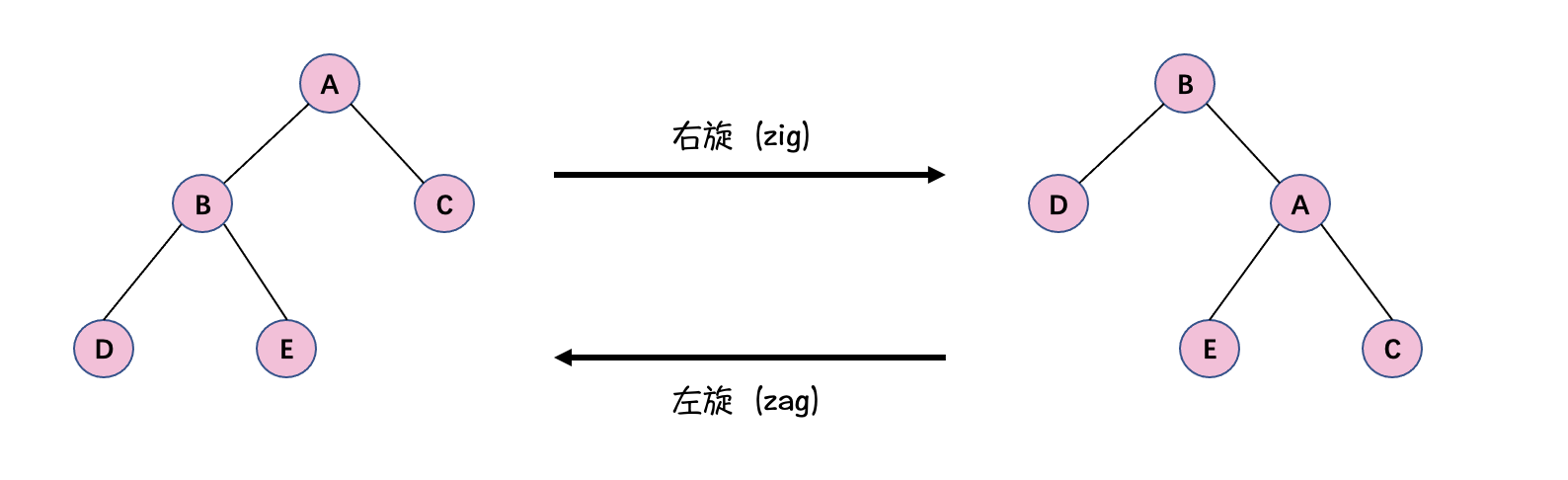
-
四种旋转情况
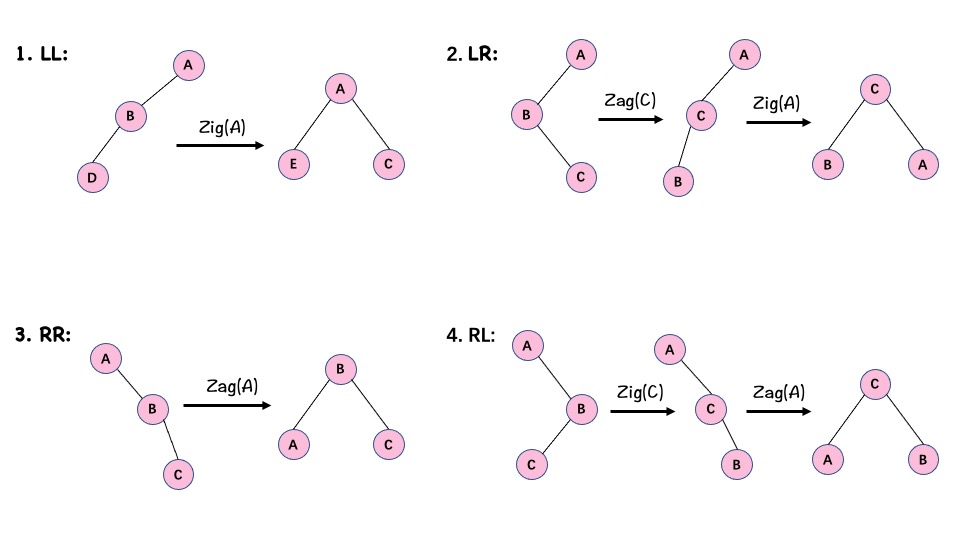


 浙公网安备 33010602011771号
浙公网安备 33010602011771号