树与二叉树
简介(Introduction)
树是由 \(n(n \ge 0)\) 个有限节点组成一个具有层次关系的集合。
二叉树 是树形结构的一个重要类型,二叉树特点是每个节点最多只能有两棵子树,且有左右之分
描述(Description)
- 树可大致分为 有根树 和 无根树 两大类
- 基本概念:
- 父亲 \((Parent)\):从一个结点到根路径上的第二个结点 —— 根结点没有父结点
- 祖先 \((Ancestor)\):对于一个结点,其父节点的父节点即为祖先节点
- 儿子 \((Child)\):如一个节点 \(v\) 为 \(u\) 的父亲,则 \(u\) 是 \(v\) 的儿子
- 度 \((Degree)\):
- 节点的度:一个节点含有的子节点的个数称为该节点的度
- 树的度:一棵树中,最大的节点的度称为树的度
- 深度 \((Depth)\):到根结点的路径上的边数
- 树的高度 \((Height)\):所有结点的深度的最大值
- 叶结点 \((Leaf)\):没有子结点的结点,度数为 \(0\) 的节点
- 兄弟 \((Brother)\):同一个父亲的多个子结点互为兄弟
- 子树 \((Subtree)\):由一个顶点(非根)以及所有后代构成的树
- 森林 \((Forest)\):多棵互不相交的树的集合称为森林,一棵树也是森林
- 二叉树的基本形态:空二叉树、单节点二叉树、左子树、右子树
- 二叉树性质:
- 在非空二叉树中,第 \(i\) 层上至多有 \(2^{i - 1}\) 个结点
- 深度为 \(k\) 的二叉树至多有 \(2^{k} - 1\) 个结点
- 对任何一棵二叉树,若其叶子结点数为 \(n_0\) ,度为 \(2\) 的结点数为 \(n_2\) ,则 \(n_0 = n_2 + 1\)
证明:
假设:度数为 \(0\) 的节点为 \(n_0\),度数为 \(1\) 的节点为 \(n_1\),度数为 \(2\) 节点为 \(n_2\)
即总点数 \(N = n_0 + n_1 + n_2\),总边数 \(E = N - 1\)
根据点的度和边点关系得,\(E = 2 * n_2 + 1 * n_1 + 0 * n_0\)
联立方程:\(n_0 + n_1 + n_2 - 1 = 2 * n_2 + 1 * n_1 + 0 * n_0\)
即,\(n_0 - 1 = n_2 \cdots \cdots \cdots \cdots \cdots \cdots \cdots 证毕.\)- \(n\) 个结点的完全二叉树深度为: \(\lfloor\log_2n\rfloor + 1\)
- 二叉树的堆式存储: 节点 \(x\) 的左儿子:\(2x\) ,右儿子:\(2x + 1\)
完全二叉树
如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树,即——深度为 \(k\),有 \(n\) 个结点的二叉树,当且仅当其每个结点都与深度为 \(k\) 的满二叉树中编号从 \(1\) 到 \(n\) 的结点一一对应
满二叉树
如果二叉树中除了叶子结点,每个结点的度都为 \(2\) ,则此二叉树称为满二叉树,即——深度为 \(k\) 且有 \(2^k - 1\) 个结点
二叉排序树
左子树上所有节点的关键字均 小于 根节点的关键字,右子树上所有节点的关键字 均大于等于 根节点的关键字;同时左子树和右子树又均是一棵二叉排序树
平衡二叉树
树上任意一个节点的左子树和右子树的深度之差不超过 \(1\)
哈夫曼树
带权路径最短的二叉树称为哈夫曼树或最优二叉树
示例(Example)
-
树
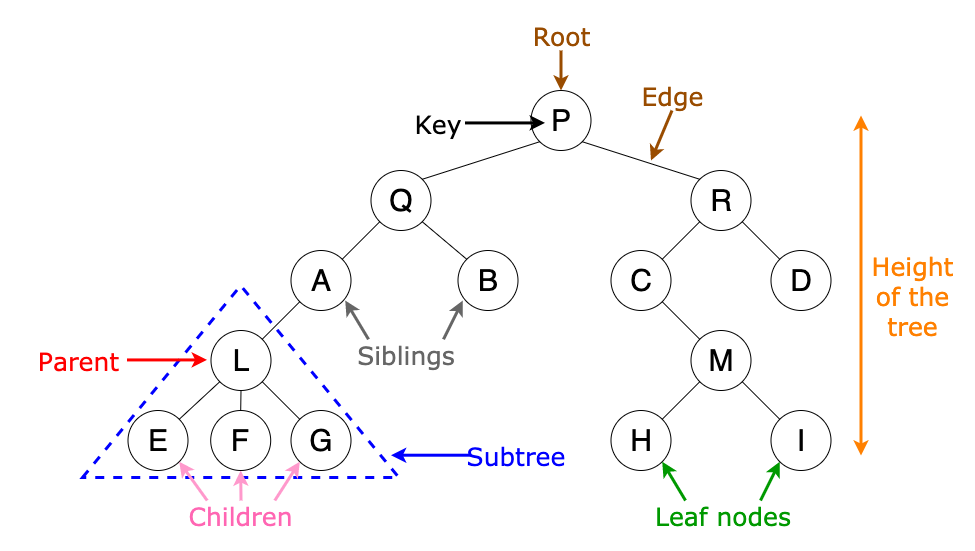
-
二叉树
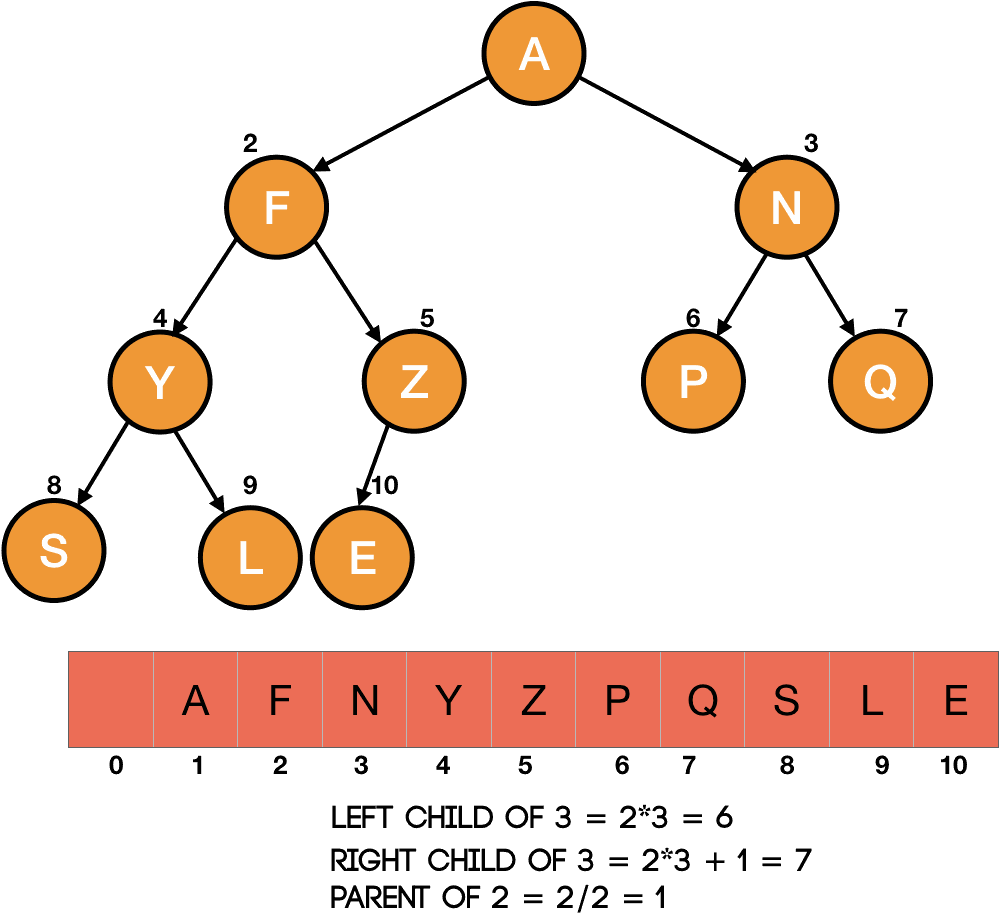
-
树的遍历
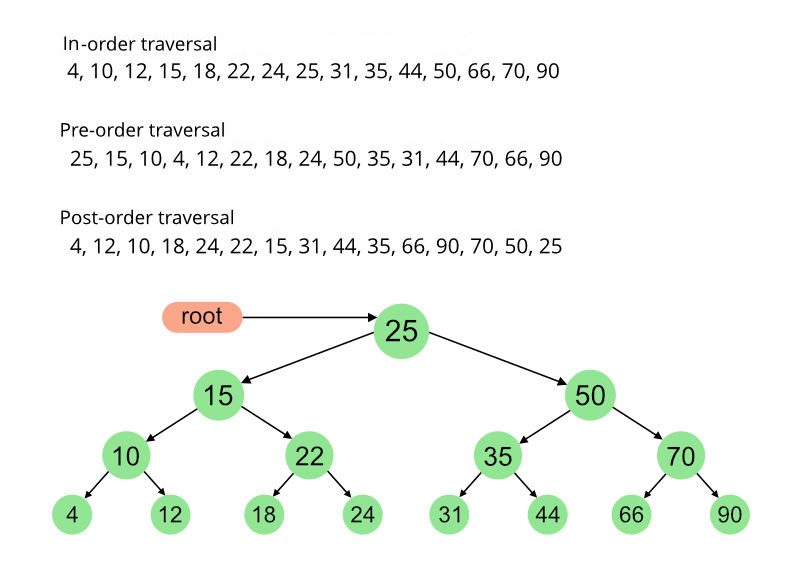
代码(Code)
-
二叉树存储方式
- 顺序存储(静态数组)方法一:
struct Tree { int val; int left, right; } tr[N];
- 顺序存储(静态数组)方法二:
/* 设当前节点:i left = a[i >> 1]; right = a[i >> 1 | 1]; val = a[i]; */ int tr[N];
- 动态(链式存储):
struct Tree { int val; Tree *left, *right; Tree() : left(NULL), right(NULL) {} Tree(int _val) : left(NULL), right(NULL), val(_val) {} };
- 顺序存储(静态数组)方法一:
-
建树
// C++ Version Tree* build(int cnt) { // 前序建树 if (!cnt) return NULL; int val; cin >> val; Tree *root = new Tree(val); root->left = build(-- cnt); root->right = build(cnt); return root; }
-
二叉树遍历
- 前序遍历: 先输出父节点,再遍历左子树和右子树
// C++ Version void pre_order(Tree *root) { if (!root) return; printf("%d ", root -> val); // 输出根节点 pre_order(root -> left); // 递归左子树 pre_order(root -> right); // 递归右子树 }
- 中序遍历: 先遍历左子树,再输出父节点,再遍历右子树
// C++ Version void in_order(Tree *root) { if (!root) return; in_order(root -> left); // 递归左子树 printf("%d ", root -> val); // 输出根节点 in_order(root -> right); // 递归右子树 }
- 后序遍历: 先遍历左子树,再遍历右子树,最后输出父节点
// C++ Version void post_order(Tree *root) { if (!root) return; post_order(root -> left); // 递归左子树 post_order(root -> right); // 递归右子树 printf("%d ", root -> val); // 输出根节点 }
- 前序遍历: 先输出父节点,再遍历左子树和右子树
应用(Application)
重建二叉树
输入一棵二叉树前序遍历和中序遍历的结果,请重建该二叉树。
- 二叉树中每个节点的值都互不相同;
- 输入的前序遍历和中序遍历一定合法;
示例:
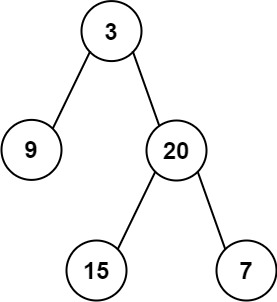
输入:
preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出:
[3,9,20,null,null,15,7]
数据范围:
\(1 \le preorder.length \le 3000\)
\(-3000 \le preorder[i], inorder[i] \le 3000\)
- 题解:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ /* 图解: pre: ______________________ ^ ^ ^ pl x pr mid ______________________ ^ ^ ^ ml pos mr 得: (pos - 1) - ml = x - (pl + 1) 即, x = pos + pl - ml */ class Solution { public: vector<int> preorder, inorder; unordered_map<int, int> rel; TreeNode* buildTree(vector<int>& _preorder, vector<int>& _inorder) { preorder = _preorder, inorder = _inorder; int n = inorder.size(); for (int i = 0; i < n; i ++ ) rel[inorder[i]] = i; return dfs(0, n - 1, 0, n - 1); } TreeNode* dfs(int pl, int pr, int ml, int mr) { if (pl > pr) return NULL; TreeNode* root = new TreeNode(preorder[pl]); int pos = rel[root->val]; root->left = dfs(pl + 1, pos + pl - ml, ml, pos - 1); root->right = dfs(pos + pl - ml + 1, pr , pos + 1, mr); return root; } };
Hint:
- “中序遍历 + 先序遍历“ 或 ”中序遍历 + 后续遍历“,都可以确定一棵二叉树,
- “先序遍历 + 后续遍历”无法确定一棵二叉树


 浙公网安备 33010602011771号
浙公网安备 33010602011771号