栈
简介(Introduction)
限定仅在 表尾进行插入和删除 操作的线性表,这一端被称为栈顶(Top),另一端称为栈底(Bottom)
描述(Description)
- 向一个栈插入新元素又称为入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素
- 从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素
示例(Example)
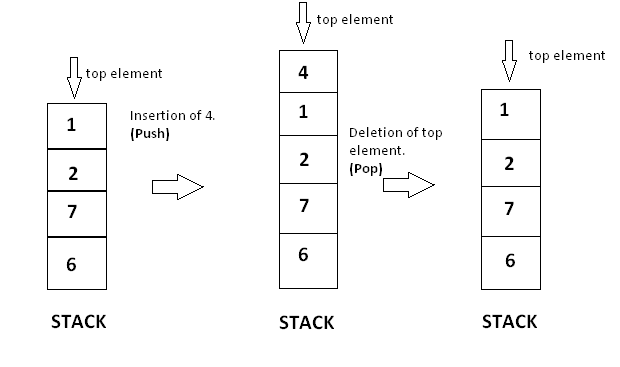
代码(Code)
// C++ Version 顺序栈
const int N = 110;
int stk[N];
// 定义栈顶
int top = 0; // top = -1;
// 新元素压入栈
stk[top ++ ] = 1; // stk[ ++ top] = 1;
// 弹出栈顶元素
-- top;
// 访问栈顶元素
stk[top - 1]; // stk[top];
// 判断栈空
top == 0; // top == -1;
// 栈中元素个数
top // top + 1
// C++ Version 链栈
#include <cstdio>
#include <iostream>
using namespace std;
struct Node {
int val;
Node *next;
Node() : next(NULL) {}
Node(int _val) : val(_val), next(NULL) {}
};
void print(Node *top) {
for (Node* p = top; p; p = p->next)
cout << p->val << ' ';
cout << endl;
}
int main() {
Node *top = NULL;
// 插入元素
Node *a = new Node(1);
a->next = top;
top = a;
Node *b = new Node(2);
b->next = top;
top = b;
print(top);
// 删除元素
Node *p = top;
top = top->next;
delete(p);
print(top);
// 判空
cout << (top == NULL) << endl;
// 栈顶
cout << top->val << endl;
return 0;
}
应用(Application)
中缀表达式求和
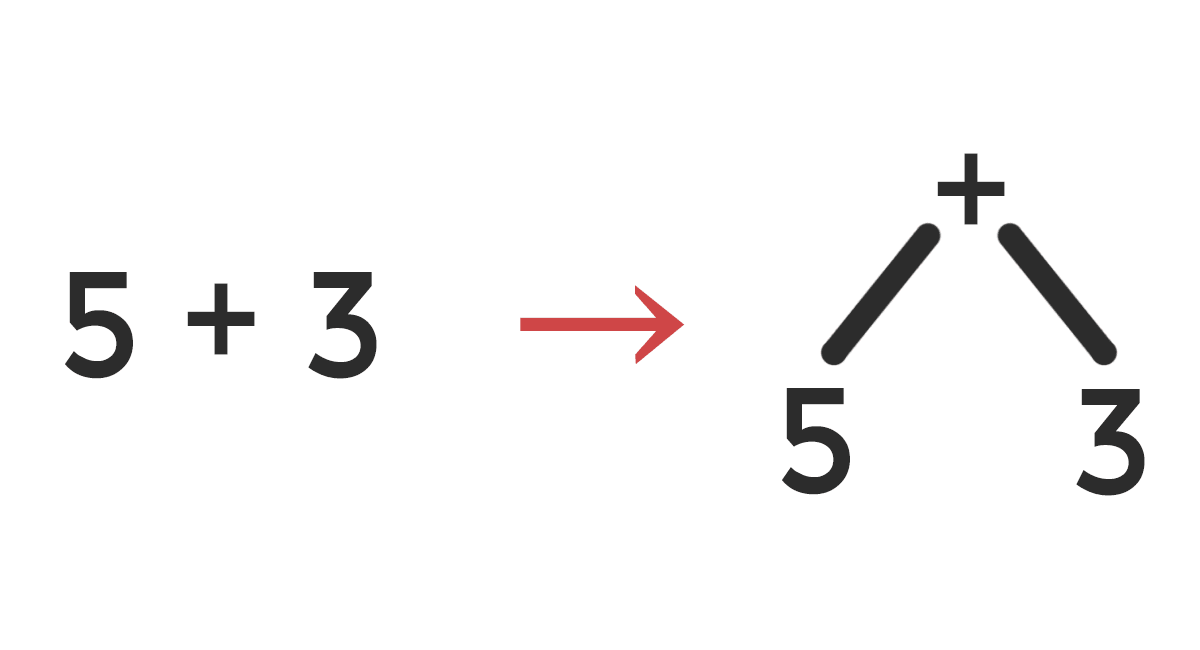
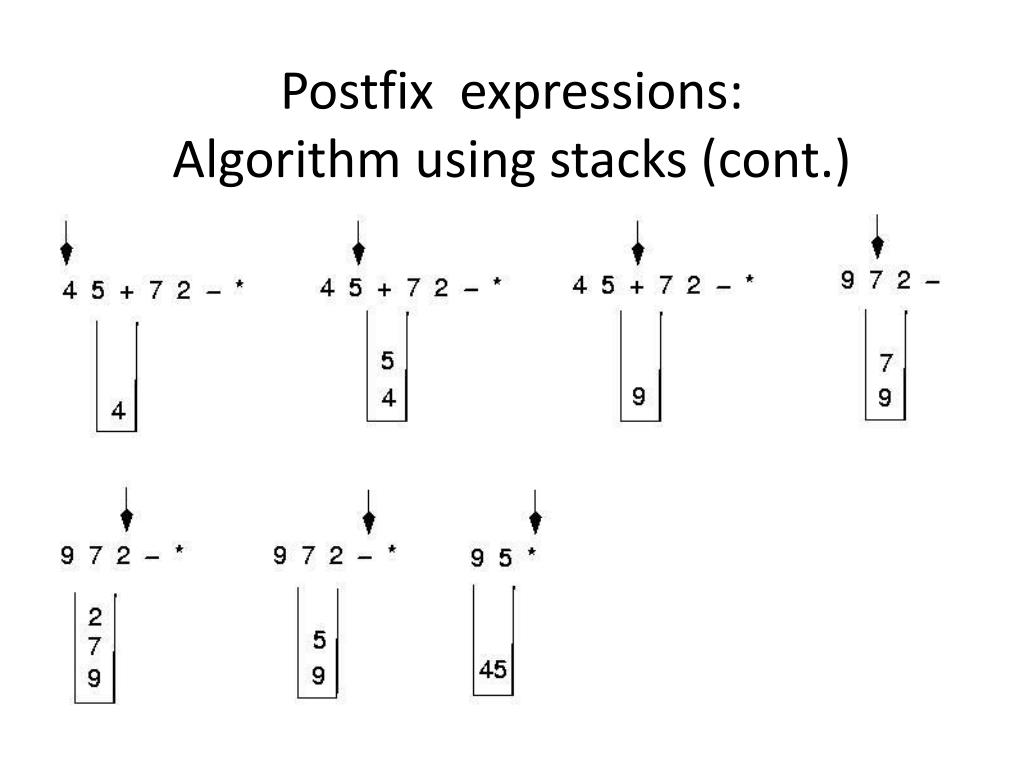
-
分析:先转化为 后缀表达式,然后通过栈进行存储并求和(后缀表达式中忽略了括号)
-
题解:
// C++ Version #include <iostream> #include <unordered_map> #include <stack> using namespace std; //设置优先级 unordered_map<char, int> h = {{'-', 1}, {'+', 1}, {'*', 2}, {'/', 2}}; stack<int> num; // 用于存所有数字 stack<char> op; // 用于存储运算符 void calc() { int b = num.top(); // 取出第二个数 num.pop(); int a = num.top(); // 取出第一个数 num.pop(); int c = op.top(); // 取出一个操作符 op.pop(); int res; //计算结果 if (c == '-') res = a - b; else if (c == '+') res = a + b; else if (c == '*') res = a * b; else if (c == '/') res = a / b; num.push(res); // 将计算后的结果加入结果集 } int main() { string s; cin >> s; for (int i = 0; i < s.size(); i ++ ) { auto c = s[i]; if (isdigit(c)) { // 将数字入栈 int x = 0, j = i; while (j < s.size() && isdigit(s[j])) // 可能出现多位数 x = x * 10 + s[j ++ ] - '0'; num.push(x); // 将 >= 1 位的数添加至num中 i = j - 1; // 更新i的位置移动到多位数的最后一位 } else if (c == '(') op.push(c); // 如果左括号直接加入op else if (c == ')') { // 遇到右括号计算括号里面的 while (op.size() && op.top() != '(') calc(); // 一直计算到左括号的位置 op.pop(); // 将左括号删除 } else { while (op.size() && h[op.top()] >= h[c]) calc(); //根据优先级进行计算 op.push(c); // 将本次的操作符进行入栈 } } while (op.size()) calc(); // 计算所有剩余的数字 cout << num.top() << endl; // 最后一个数即为答案 return 0; }
中缀转后缀表达式
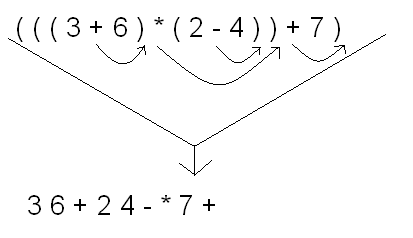
-
题解:
#include <iostream> #include <unordered_map> #include <stack> using namespace std; stack<char> op; void calc() { char c = op.top(); op.pop(); cout << c << ' '; } int main() { string s; cin >> s; unordered_map<char, int> pr = {{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}}; for (int i = 0; i < s.size(); i ++ ) { if (isdigit(s[i])) { int j = i, x = 0; while (j < s.size() && isdigit(s[j])) x = x * 10 + s[j ++ ] - '0'; cout << x << ' '; i = j - 1; } else if (s[i] == '(') op.push(s[i]); else if (s[i] == ')') { while (op.size() && op.top() != '(') calc(); op.pop(); } else { while (op.size() && op.top() != '(' && pr[op.top()] >= pr[s[i]]) calc(); op.push(s[i]); } } while (op.size()) calc(); return 0; }
括号匹配
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = "()"
输出:true
示例 2:
输入:s = "()[]{}"
输出:true
示例 3:
输入:s = "(]"
输出:false
提示:
\(1 \le s.length \le 10^4\)
\(s\) 仅由括号 (),[],{}组成
-
题解:
// C++ Version class Solution { public: bool isValid(string s) { stack<char> stk; for (int i = 0; i < s.size(); i ++ ) { if (s[i] == '(' || s[i] == '{' || s[i] == '[' || s[i] == '<') stk.push(s[i]); else { if (stk.size() && s[i] == ')' && stk.top() == '(') stk.pop(); else if (stk.size() && s[i] == '}' && stk.top() == '{') stk.pop(); else if (stk.size() && s[i] == ']' && stk.top() == '[') stk.pop(); else if (stk.size() && s[i] == '>' && stk.top() == '<') stk.pop(); else return false; } } return stk.empty(); } };


 浙公网安备 33010602011771号
浙公网安备 33010602011771号