2021.5.29 开心赛（背包经典题） （下）

6、最小乘车费用（这题我在洛谷没找到）

• 题目描述
  
  假设某条街上每 一公里 就有一个公共汽车站，并且乘车费用如下表： 
  
  公里数 1 2 3 4 5 6 7 8 9 10
  费用 12 21 31 40 49 58 69 79 90 101 
  
  而任意一辆汽车从不行驶超过 10 公里 。某人想行驶 n(1<=n<=100) 公里，假设他可以任意次换车，请你帮他找到一种乘车方案，使得总费用最小 
  
  
  注意： 10 公里 的费用比 1 公里 小的情况是允许的。 
  
  
  输入
  
  共两行，第一行为 10 个不超过 200 的整数，依次表示行驶 1 ～ 10 公里的费用，相邻两数间用一个空格隔开；第二行为某人想要行驶的公里数。
  
   
  
  输出
  
  仅一行，包含一个整数，表示行使这么远所需要的最小费用。 
  
  
  样例输入
  
  12 21 31 40 49 58 69 79 90 101
  15
  
  样例输出
  
  147

   

• 心路历程（跟殳哥学的）：这题是个完全背包。蒟蒻如我在判断出来类型之后就卡住了，样例都过不了，后来发现自己没赋初值就用min了……我已经习惯了自己犯各种各样奇葩错误了……
• 代码实现：

  #include <bits/stdc++.h>
  using namespace std;
  long long w[15];
  long long m;
  long long dp[2005]={};
  int main()
  {
      for(int i=1;i<=10;i++)
      {
          scanf("%lld",&w[i]);
      }
      scanf("%lld",&m);
      
      dp[0]=0;
      for(int i=1;i<=m;i++)
      {
          dp[i]=1<<30;
          for(int j=1;j<=10;j++)
          {
              if(i>=j)
              {
                  dp[i]=min(dp[i-j]+w[j],dp[i]);//i和j！！！！ 
              }
          }
      }
      printf("%lld",dp[m]);
      return 0;
                  

   

7、质数和分解

• 心路历程：这题最开始卡了我好久，后来发现自己素数筛写错了……然后就没什么了。
• 代码实现：

  #include <bits/stdc++.h>
  using namespace std;
  int n;
  int isprime[1005];
  int dp[2005];
  
  bool prime(int x)
  {
      for(int i=2;i<=sqrt(x);i++)
      {
              if(x%i==0)
              {
                  return 0;
              }
          
          }
      return 1;//函数结果写外面！！！！ 
  }
  int main()
  {
      while(cin>>n)
      {
          int w=0;
          for(int i=2;i<=n;i++)
          {
              if(prime(i))
              {
                  w++;
                  isprime[w]=i;
              }
          }
          memset(dp,0,sizeof(dp));
          dp[0]=1;
  
          for(int i=1;i<=w;i++)
          {
              for(int j=isprime[i];j<=200;j++)
              {
                  dp[j]+=dp[j-isprime[i]];
              }
          }
          cout<<dp[n]<<endl; 
      }
      return 0;
  }

   

8、逃亡的准备

【问题描述】
　　在《Harry Potter and the Deathly Hallows》中，Harry Potter他们一起逃亡，现在有许多的东西要放到赫敏的包里面，但是包的大小有限，所以我们只能够在里面放入非常重要的物品。现在给出该种物品的数量、体积、价值的数值，希望你能够算出怎样能使背包的价值最大的组合方式，并且输出这个数值，赫敏会非常感谢你。
【输入格式】
　　第1行有2个整孰物品种数n和背包装载体积v；
　　第2行到i+l行每行3个整数，为第i种物品的数量m、体积w、价值s。
【输出格式】
　　仅包含一个整数，即为能拿到的最大的物品价值总和。
【输入样例】
　　2 10
　　3 4 3
　　2 2 5
【输出样例】
　　13
　　样例说明：选第一种一个，第二种两个，结果为3×1+5×2=13。
【数据规模】
　　对于30%的数据：1≤v≤500;1≤n≤2000;l≤m≤10;1≤w≤20;1≤s≤100;
　　对于lOffl6的数据：1≤v≤500;1≤n≤2000;1≤m≤5000;1≤w≤20;1≤s≤100。

 

• 心路历程：一眼就是板子题。卡了三十分之后，听机房大佬说，这题卡常数，要加特判。我又看了其他人的博客，发现很多人用二进制拆分。
  
  
• 代码实现：

  #include <bits/stdc++.h>
  using namespace std;
  int n,v;
  int s[2005],w[2005],m[2005];
  int dp[10005]={};
  
  int main()
  {
      scanf("%d %d",&n,&v);
      for(int i=1;i<=n;i++)
      {
          scanf("%d %d %d",&m[i],&w[i],&s[i]);    
      }
      
      for(int i=1;i<=n;i++)
      {
          for(int j=v;j>w[i];j--)
          {
              for(int k=1;k<=m[i];k++)
              {
                  if(k*w[i]<=j)
                  {
                      dp[j]=max(dp[j],dp[j-k*w[i]]+k*s[i]);
                  }
                  else
                  {
                      break;//如果只取一个都不行，那后面就没有再看的意义了
                  }
              
              }
          }
      }
      printf("%d",dp[v]);
      return 0;
  }
  /*
  2 10
  3 4 3
  2 2 5
  */

   

4、暗黑游戏

 

 

 

 

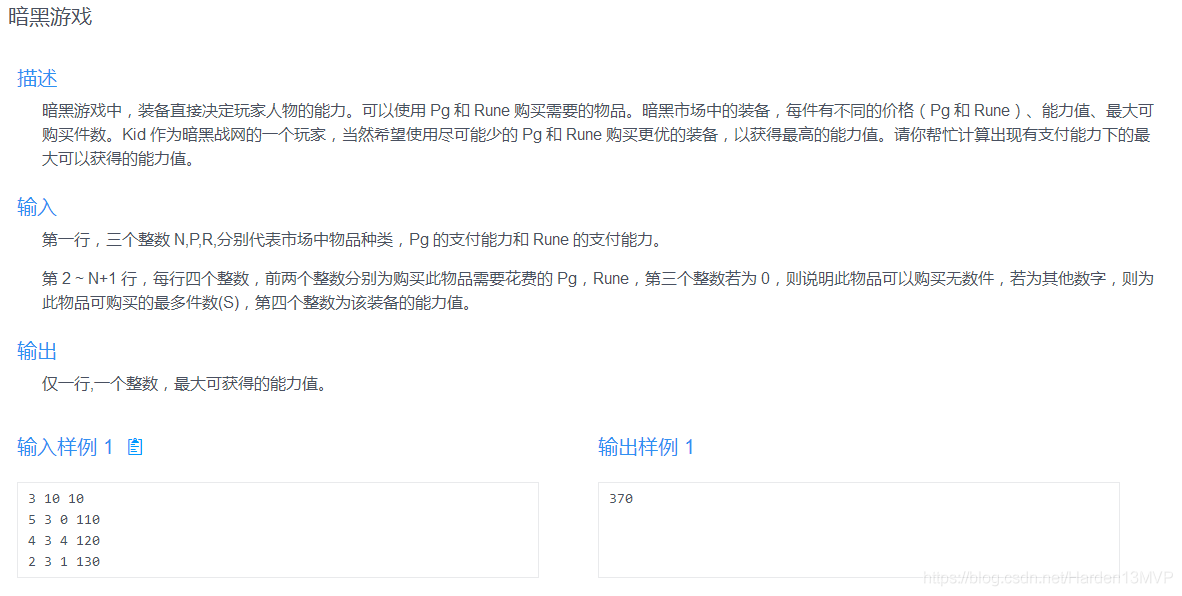
• 这题我被卡了四十分！

• #include <bits/stdc++.h>
  using namespace std;
  int pg, ru, n;
  int p[500], r[500], k[500], c[500];
  int dp[2005][2005] = {};
  
  int main() {
      scanf("%d %d %d", &n, &pg, &ru);
      for (int i = 1; i <= n; i++) {
          scanf("%d %d %d %d", &p[i], &r[i], &k[i], &c[i]);
      }
  
      for (int i = 1; i <= n; i++) {
          if (k[i] == 0) {
              for (int j = pg; j >= p[i]; j--) {
                  for (int h = ru; h >= r[i]; h--) {
                      dp[j][h] = max(dp[j][h], dp[j - p[i]][h - r[i]] + c[i]);
                  }
              }
          } else {
              for (int j = pg; j >= p[i]; j--) {
                  for (int h = ru; h >= r[i]; h--) {
                      for (int w = 0; w <= k[i]; w++) {
                          if (w * p[i] <= j && w * r[i] <= h) {
                              dp[j][h] = max(dp[j][h], dp[j - w * p[i]][h - w * r[i]] + w * c[i]);
                          }
                      }
                  }
              }
          }
      }
  
      printf("%d", dp[pg][ru]);
      return 0;
  }
  /*
  3 10 10
  5 3 0 110
  4 3 4 120
  2 3 1 130
  */