有向面积

首先先讨论一下，对于一个三角形如何求面积：

 

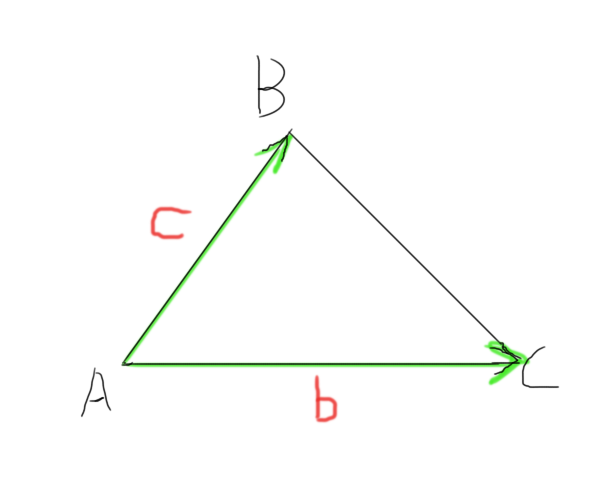
很明显，S = |b| * |c| * |sinA| / 2 = | b × c | / 2;

学过叉积的都懂，由三角形的两个边向量就可以求出面积， 那么对于一个多边形呢（不规则的那种）：

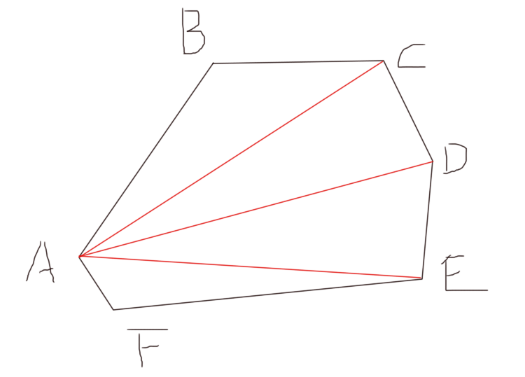
可以分解为S△ABC+S△ACD+S△ADE+S△AEF；

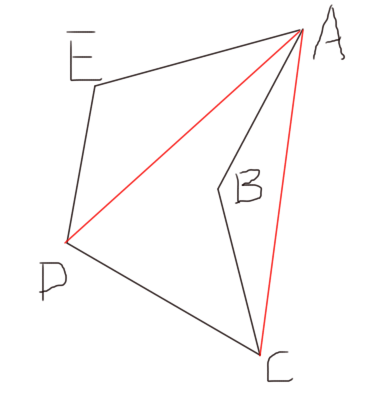
这个假如分解出来的话，单纯的看面积会重复算S△ABC，所以引入有向面积的概念；

简单点说，回到三角形的问题上，三角形的面积能够用叉积来表示，但是这个叉积是取模的，现在顺时针读取多边形的顶点来构造三角形，将他们的叉积相加，就能得到这个多变性的总面积了。

比如上图，S△ABC + S△ACD + S△ADE中，△ABC的叉积是和另外两个相反的，正好可以抵消掉，最后结果取模就是多边形的面积。

 

 

例如HDU2036

#include<iostream>
#include<cstdio>
#include<string.h>
#include<math.h>
#include<string>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<queue>
#include<iomanip>
using namespace std;
struct P{
    int x;
    int y;
};
P p[105];
double area(int a)
{
    int b = a-1;
    return (p[b].x*p[a].y-p[a].x*p[b].y)-(p[0].x*p[a].y-p[a].x*p[0].y)+(p[0].x*p[b].y-p[b].x*p[0].y);
}
int main()
{
    int n;
    while(cin >> n){
        if(n==0) break;
        for(int i=0;i<n;i++)
            cin >> p[i].x >> p[i].y;
        double sum = 0;
        for(int i=2;i<n;i++){
            sum += 1.0/2.0*area(i);
        }
        cout << fixed << setprecision(1) << sum << endl;
    }
    return 0;
}