KMP、扩展KMP、MANACHER
一、KMP
作用:用于在一个文本串S内查找一个模式串P出现的位置
string str = "bacbababadababacambabacaddababacasdsd"; string ptr = "ababaca";
如上图,可得在第10与26处包含ptr数组;
暴力做法:暴力for,碰到不一样的直接返回,从后一个开始继续for,最差能到O(n * m)
KMP 做法:
主要的思路是跳,比如你一开始从上面例子里的bacbababadababacambabacaddababacasds红色开始的地方a开始,扫到后面发现有不匹配了,再扫一遍babad就很亏了,所以KMP主要就是维护你扫过的段落中已经符合的部分,最大化利用已经搜索过的部分;
(https://www.bilibili.com/video/av14051190?from=search&seid=15099112676954896179可以看一看这个印度小哥的讲解,还是很清楚的)
KMP的关键在于NEXT数组,整个KMP都是这个数组撑起来的,主要的含义就是一个固定字符串的最长前缀和最长后缀相同的长度。
比如:abcjkdabc 最长前缀和最长后缀相同的为abc:
cbcbc最长前缀和最长后缀为cbc;
abcbc最长前缀和最长后缀为。。。(划掉)/*最长前缀是从第一个字符开始但是不包括最后一个字符,比如aaa最长前缀为aa*/
NEXT数组维护的结果就是
/*目标字符串是ababaca*/ NEXT[0] = -1; NEXT[1] = 0;"a" NEXT[2] = 0;"ab" NEXT[3] = 1;"aba" NEXT[4] = 2;"abab" NEXT[5] = 3;"ababa" NEXT[6] = 0;:ababac"
NEXT[7] = 1;""ababaca"
(先注意一下NEXT数组是一个近似连续与周期性之间的,递增的时候不会跳,永远是+1,+1,至于为什么后面会有)
注意!别当成回文串!
NEXT数组效用如下:
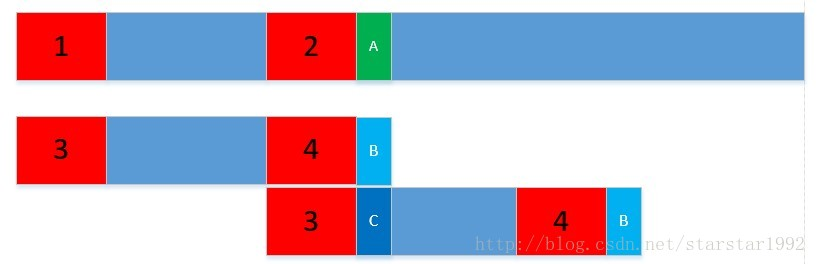
对上图而言,上面一条是目标数组,下面一条是标准数组,假如1和2是NEXT维护过的相同的最大前缀和最大后缀,相对应的34也是相同的,然而扫到A和B时发现了不相同,这个时候重新回去扫就是亏到爆炸的,然而因为有维护最大前缀的关系(可以看出来中间蓝色的一段肯定是没有匹配的的,next数组也顺便保证了这一点),可以直接跳过中间那一段距离,直接将3移动到4的位置,大大降低了复杂度(多数情况);
模板(来自kuagnbin大大)
#include<cstdio>
#include<iostream>
#include<string>
using namespace std;
const int maxn = 1000002;
string S;//主串
string T;//模式串
int NEXT[maxn];//当前位置如果不匹配则指针回溯的位置即最长前后缀相同的长度
int slen, tlen;
void getnext()//生成next数组
{
//a b a c a b a d a b a c a b a
int j, k;//j是模式串的当前角标,k是在模式串当前角标之前已经匹配的前缀后缀的长度
j = 0; k = -1; NEXT[0] = -1;
/*已知的next[j]和k一位置T[0]T[1]...T[k - 1]=T[j - k]T[j - k + 1]....T[j - 1];
推算next[j+1]则将T[j]与T[k]比较(即判断该位置是否能接着前后缀相同)
若T[k] == T[j] 则T[0] ..... T[k] = T[j - k] ... T[j-1]
即next[++j] = ++k;意味着已匹配的前后缀长度加1之后,T[0..j]拥有k+1的相同前后缀
也就是在j+1位与其不匹配时,就返回第k+1位,即相同的前缀的后一位
若T[k] != T[j] 即不匹配时,不可能一棍子打死从0开始,退一步找一个相对短的匹配前缀
k代表的是目前为止相同前后缀的长度,若当前j不匹配,则将k跳回next[k]处
可以理解为T数组自己对自己用next已经记录的部分匹配,既然k处不匹配了
相当于前缀在k处与自己失配,将k前移回上一个能够匹配的前缀长度,判断是否能适配现在的T[j]
就像已经适配的前缀是ababac 后缀是ababab,发现b和c不相同,回溯一次前缀为ababa
最后一位a仍然与当前T[j] = b,不相同,再回溯一次为b与当前相同,就继续开始判定了
这里说一下默认的是next[k] = k-1;这一点通过相同时可以很容易看出来,但是不够全面,所以使用k = next[k];而不是k--*/
while (j < tlen)
{
if (k == -1 || T[j] == T[k])
NEXT[++j] = ++k;
else
k = NEXT[k];
}
}
int KMP_index()//读取出现的位置(第一个)
{
int i = 0, j = 0;//i指向主串,j指向模式串,i不会回退
getnext();
while (i < slen && j < tlen)
{
if (j == -1 || S[i] == T[j])
{
i++;
j++;
}
else
{
j = NEXT[j];
}
}
if (j == tlen)
return i - tlen;
else return -1;
}
int KMP_Count()//出现的次数
{
int ans = 0;
int i, j = 0;
if (slen == 1 && tlen == 1)
{
if (S[0] == T[0])
return 1;
else return 0;
}
getnext();
for (i = 0; i < slen; i++)
{
while (j > 0 && S[i] != T[j])
j = NEXT[j];
if (S[i] == T[j])
j++;
if (j == tlen)
{
ans++;
j = NEXT[j];
}
}
return ans;
}
int main()
{
int TT;
int i, cc;
cin >> TT;
while (TT--)
{
cin >> S >> T;
slen = S.length();
tlen = T.length();
cout << "模式串T在主串S中首次出现的位置是: " << KMP_index() << endl;
cout << "模式串T在主串S中出现的次数为: " << KMP_Count() << endl;
for (int i = 0; i < tlen; i++)
cout << NEXT[i] << " ";
}
return 0;
}
二、扩展KMP
给出一个长为N的字符串S,再给出一个长为M的字符串T
求S的所有后缀中和T的最长公共前缀
运用KMP的思想,衍生出了Extend-KMP算法
类似的,用next数组保存T[i....M-1]与T的最长公共前缀
extend[i]表示了T与S[i,n-1]的最长公共前缀
但是有一个特例:next[0] = len;
举个栗子:
string T = "aaaabaaaa";
这个字符串长度为9,则对应的NEXT如下
next下标 0 1 2 3 4 5 6 7 8
value 9 3 2 1 0 4 3 2 1
string 略 aaa aa a none aaaa aaa aa a
下面来详细讲一下扩展KMP算法
定义的数组:
next[i]表示满足T[i ....i + z - 1] == T[0 ...... z - 1]的最大的z值(也就是T[i....M-1]与T的最长公共前缀)
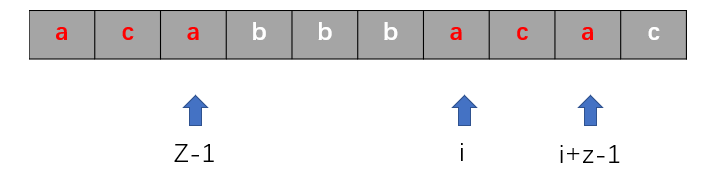
上图的next[6] = 4;
设P为A串中匹配到的最远位置,K为让其匹配到最远位置的值;

P = k + extend[k] - 1;(extend[i]表示了T与S[i,n-1]的最长公共前缀)翻译过来就是匹配到的位置(k) + 向后延伸过去的最长公共前缀的长度-1;此时的P是最大的,但K不一定是最大的!
根据extend的定义可得S[k .. P] = T[0 ... p - k](分别意义是前缀,相同的那种);
设 i > k 所以又有S[i .... P] = T[i - k ... p - k],(即对于S上k到P任意一点都会有对应的前缀相同,因为是包含在相同前缀S[k .. P] = T[0 ... p - k]中的)
设L = next[i - k],则根据next定义有T[0 ..... (L - 1)] = T[(i - k )...... (i - k )+(L - 1)];(就是前面的定义)
接下来讨论(i - k )+ (L - 1) 与 L - 1 的关系,也可以等同于(i - k) + ( L - 1)与(p - k)的关系
1) i - k + L - 1 < p - k时即i + L <= p时,相当于下图的情况
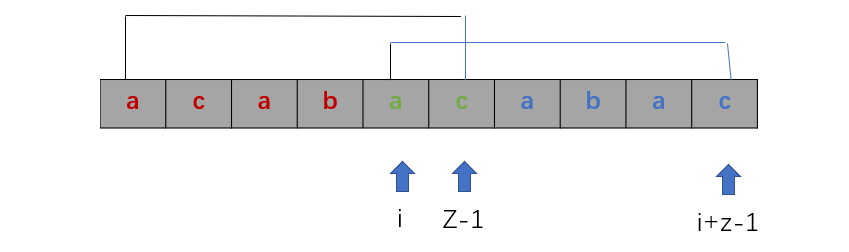
此时由S[k ...p] = T[0 ..... p - k]可以得到S[i.......i + L - 1] = T[i - k ..... i - k + L - 1];
又因为T[0 .... L - 1] = T[i - k ... i - k + L - 1],所以S[i ... i + L - 1] = T[0 .... L - 1];这说明ex[i] >= L
又因为由next定义可得S[i + L] 必然不等于T[L](否则next值应该更大),所以ex[i] = L;
2)i + k - L + 1 >= p - k
首先 S[i ... p] 和 T[0 ..... p - i]是相等的,
然后对于S[p + 1] 和T[ p - i + 1]是否否相等是不知道的,因为P是匹配的最远位置,在P之后无法知道其他匹配信息
所以要从此时往后继续匹配。
对于next数组,是自身匹配,类似KMP,唯一不同的地方在边界上,0的位置直接可以知道是lenT,next【1】的值需要预先求出然后初始k = 1, p = extend[1];
需要注意的是,在上述情况2中,本该从S[p+ 1]与T[p - i + 1]开始匹配,但是,如果p + 1 < i 时(据说是存在的,当extend[i - 1] = 0 且前面的extend值都没有延伸到 i 之后的时候),需要将S,T的下标都+1(此时P必然等于i - 2,如果A、 B的下标用两个变量控制,都要+1);
模板:
#include<cstdio> #include<iostream> #include<algorithm> using namespace std; //next[i] : x[i .... m - 1]与x[0 .... m-1]的最长公共前缀 //extend[i]: y[i ... n - 1] 与x[0 .... m - 1]的最长公共前缀 void get_next(char *x, int m, int *next)//m为子串长度,x为目标子串 { next[0] = m; int j = 0; //初始化next[1] while (j + 1 < m && x[j] == x[j + 1]) j++; next[1] = j; //推导之后的值 int k = 1; for (int i = 2; i < m; i++) { int p = next[k] + k - 1; int L = next[i - k]; if (i + L < p + 1) next[i] = L; else { j = max(0, p - i + 1); while (i + j < m && x[i + j] == x[j]) j++; next[i] = j; k = i; } } } void ExKMP(char *x, int m, char *y, int n, int *next, int *extend) { get_next(x, m, next); int j = 0; while (j < n && j < m && x[j] == y[j]) j++; extend[0] = j; int k = 0; for (int i = 1; i < n; i++) { int p = extend[k] + k - 1; int L = next[i - k]; if (i + L < p + 1) extend[i] = L; else { j = max(0, p - i + 1); while (i + j < n && j < m && y[i + j] == x[j]) j++; extend[i] = j; k = i; } } }
三、KMP最小循环节
KMP最小循环节、循环周期:
定理:假设S的长度为len,则S存在最小循环节,循环节的长度L为len-next[len],子串为S[0…len-next[len]-1]。
(1)如果len可以被len - next[len]整除,则表明字符串S可以完全由循环节循环组成,循环周期T=len/L。
(2)如果不能,说明还需要再添加几个字母才能补全。需要补的个数是循环个数L-len%L=L-(len-L)%L=L-next[len]%L,L=len-next[len]。
https://blog.csdn.net/hao_zong_yin/article/details/77455285

https://www.cnblogs.com/yym2013/p/3586495.html
//后面的鸽了
四、马拉车算法(Manacher)
给定一个字符串,求出其最长回文子串;
暴力解法:枚举每一个字符,以其为中心向两边查找;
Manacher:由于回文串分为偶回文和奇回文,并且在处理奇偶的问题上会比较繁琐,所以可以使用 一个技巧:在字符串的首尾,及各字符间插入一个字符(必须是没有出现过的);
例如:对于字符串“abcba”为奇回文,可以扩充为"$#a#b#c#b#a#",可以发现除去第一位标记位后
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn = 110010;
//转换原始串
int INIT(char *st, char *tmp)
{
int i, len = strlen(st);
tmp[0] = '@';//字符串开头增加一个特殊字符,防止越界
for (i = 1; i <= 2 * len; i += 2)
{
tmp[i] = '#';
tmp[i + 1] = st[i / 2];
}
tmp[2 * len + 1] = '#';
tmp[2 * len + 2] = '$';//字符串结尾加一个字符,防止越界
tmp[2 * len + 3] = 0;
return 2 * len + 1;//返回转换字符串的长度
}
//Manacher算法计算过程
int MANACHER(char *st, int len, int *Len)
{
int mx = 0, ans = 0, po = 0;//mx即为当前计算回文串最右边字符的最大值
for (int i = 1; i <= len; i++)
{
if (mx>i)
Len[i] = min(mx - i, Len[2 * po - i]);//在Len[j]和mx-i中取个小
else
Len[i] = 1;//如果i>=mx,要从头开始匹配
while (st[i - Len[i]] == st[i + Len[i]])
Len[i]++;
if (Len[i] + i>mx)//若新计算的回文串右端点位置大于mx,要更新po和mx的值
{
mx = Len[i] + i;
po = i;
}
ans = max(ans, Len[i]);
}
return ans - 1;//返回Len[i]中的最大值-1即为原串的最长回文子串额长度
}
int main()
{
char str[maxn];//原字符串
while (cin >> str)
{
char tmp[maxn << 1];//转换后的字符
int Len[maxn << 1];
int len = INIT(str, tmp);
cout << MANACHER(tmp, len, Len) << endl;
}
}


