test20190818
闲扯
哇,今天的考试好迷啊,题解都没有。。
\(T1\) 没想到能多次向一个点派送士兵,然后就只过了最后连个用来 \(hack\) 的点???
\(T2\) 一道神仙数学题,机房的 \(dalao\) 们讨论了两节课还没结果,现在还在改。。
\(T3\) 我第一反应就是网络流,但是不知道怎么建图,结果是两颗 \(Trie\) 树,在节点连边,然后找最小割。。。之前嫌麻烦就没去学,有点后悔啊。。。
题面
\(T1\)
Solution
我们可以发现,对于每一个派送 \(k\) 个士兵的节点 \(x\) ,产生的价值为 \(size_x\times k+\sum dep_i\) 。其中 \(size\) 为以 \(1\) 为根结点时,以 \(x\) 为根节点的子树的大小, \(dep_i\) 表示该子树中的节点 \(i\) 到 \(x\) 的距离。
需要注意的是,当一个点被派送了多次士兵时,不能简单地对 \(k\) 进行累加,事实上,新的贡献为 \(size_x\cdot \sum k+m\cdot \sum dep_i\) 。
因为答案是和根结点有关的,考虑换根。
先用 \(DFS\) 维护出此时每一个点的 \(\sum dep_i\) 和子树大小 \(size_x\) 。
然后对于每一次派送,增加的答案计入总数,同时统计对这个点一共派送了的次数也派送士兵的总数。
然后再用一个 \(DFS\) 来进行换根操作。
经过分析可以得知,每一次换根时,对答案有影响的点只会是当前根节点和即将转移到的点,当且仅当有向该点派送过士兵时成立。(因为其他点都已经在某颗子树中了,不会以它为子树的根节点产生新的贡献)不知道 解释清楚没,凑合着看吧
转移时,我们先将新的根结点对当前根节点的贡献减掉,然后再加上换根之后新产生的贡献,统计答案。具体如下:
新的根结点对当前根节点的贡献:( \(cs\) 表示 \(rt\) 这个点派送得次数, \(ex\) 表示 \(\sum dep_i\) , \(add\) 表示 \(\sum k\) )
\(val=cs_{rt}*(ex_{to}+size_{to})+add_{rt}*size_{to}\)
同时因为换了新的根,所以 \(\sum dep_i\) 可能会发生变化,也需要更新:
\(ex_{to}=ex_{rt}+n-2*size_{to}\)
产生的新的贡献为:(其中 \(exval\) 表示以 \(1\) 为根时的 \(ex\) )
\(cs_{to}*(ex_{rt}-exval_{to})+add_{to}*(n-size_{to})\)
然后,找到最小解和对应的所有节点,排序后输出即可。
Code
#include<bits/stdc++.h>
#define del(a,i) memset(a,i,sizeof(a))
#define ll long long
#define inl inline
#define il inl void
#define it inl int
#define ill inl ll
#define re register
#define ri re int
#define rl re ll
#define mid ((l+r)>>1)
#define lowbit(x) (x&(-x))
#define INF 0x3f3f3f3f
using namespace std;
template<class T>il read(T &x){
int f=1;char k=getchar();x=0;
for(;k>'9'||k<'0';k=getchar()) if(k=='-') f=-1;
for(;k>='0'&&k<='9';k=getchar()) x=(x<<3)+(x<<1)+k-'0';
x*=f;
}
template<class T>il print(T x){
if(x/10) print(x/10);
putchar(x%10+'0');
}
ll mul(ll a,ll b,ll mod){long double c=1.;return (a*b-(ll)(c*a*b/mod)*mod)%mod;}
it qpow(int x,int m,int mod){
int res=1,bas=x%mod;
while(m){
if(m&1) res=(res*bas)%mod;
bas=(bas*bas)%mod,m>>=1;
}
return res%mod;
}
const int MAXN = 5e5+5;
int n,m,u,v,x,k,head[MAXN],num_edge,cap[MAXN],num;
struct Edge{
int next,to;
Edge(){}
Edge(int next,int to):next(next),to(to){}
}edge[MAXN<<1];
il add_edge(int u,int v){
edge[++num_edge]=Edge(head[u],v),head[u]=num_edge;
edge[++num_edge]=Edge(head[v],u),head[v]=num_edge;
}
int f[MAXN],sz[MAXN],add[MAXN],cs[MAXN];
ll ex_val[MAXN],ans;
bool tr[MAXN];
il DFS(int u,int fa){
f[u]=fa,sz[u]=1;
for(ri i=head[u];i;i=edge[i].next){
if(edge[i].to==fa) continue;
DFS(edge[i].to,u);sz[u]+=sz[edge[i].to];
ex_val[u]+=ex_val[edge[i].to]+sz[edge[i].to];
}
}
il DFS1(int u,ll val,ll ex){
if(tr[u]) val+=1ll*cs[u]*(ex-ex_val[u])+1ll*add[u]*(n-sz[u]);
if(val==ans) cap[++num]=u;
else if(val<ans) ans=val,cap[num=1]=u;
for(ri i=head[u];i;i=edge[i].next){
if(edge[i].to==f[u]) continue;
rl tval=val-(tr[u]?1ll*cs[u]*(ex_val[edge[i].to]+sz[edge[i].to])+1ll*add[u]*sz[edge[i].to]:0);
rl tex=ex-2*sz[edge[i].to]+n;
DFS1(edge[i].to,tval,tex);
}
}
int main()
{
freopen("A.in","r",stdin);
freopen("A.out","w",stdout);
read(n),read(m);
for(ri i=1;i<n;++i) read(u),read(v),add_edge(u,v);
DFS(1,0);
for(ri i=1;i<=m;++i) read(x),read(k),tr[x]=1,add[x]+=k,cs[x]++,ans+=1ll*k*sz[x]+ex_val[x];
cap[++num]=1;rl tmp=ans;
for(ri i=head[1];i;i=edge[i].next){
rl val=tmp-(tr[1]?1ll*cs[1]*(ex_val[edge[i].to]+sz[edge[i].to])+1ll*add[1]*sz[edge[i].to]:0);
rl ex=ex_val[1]+n-2*sz[edge[i].to];
DFS1(edge[i].to,val,ex);
}
printf("%lld\n",ans);sort(cap+1,cap+1+num);
for(ri i=1;i<=num;++i) printf("%d ",cap[i]);
return 0;
}
\(T2\)
Solution
将每次变换看做一个矩阵,转化为矩阵的 \(BSGS\) .
由于矩阵可能没有逆,所以最后再判一下解是否合法.
时间复杂度 \(O(T\cdot \sqrt{P}\ \cdot log\sqrt{P})\) 。
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int read()
{
int out=0,fh=1;
char jp=getchar();
while ((jp>'9'||jp<'0')&&jp!='-')
jp=getchar();
if (jp=='-')
fh=-1,jp=getchar();
while (jp>='0'&&jp<='9')
out=out*10+jp-'0',jp=getchar();
return out*fh;
}
int k,b,x0,P;
int add(int a,int b)
{
return (a+b>=P)?(a+b-P):(a+b);
}
int mul(int a,int b)
{
return 1LL * a * b % P;
}
typedef pair<int,int> pii;
struct Matrix
{
int v[2][2];
pii Hash()
{
return make_pair(v[0][0],v[1][0]);
}
Matrix(){memset(v,0,sizeof v);}
Matrix operator * (const Matrix &rhs) const
{
Matrix res;
for(int k=0;k<2;++k)
for(int i=0;i<2;++i)
if(v[i][k])
for(int j=0;j<2;++j)
res.v[i][j]=add(res.v[i][j],mul(v[i][k],rhs.v[k][j]));
return res;
}
/*void pr()
{
for(int i=0;i<2;++i)
{
for(int j=0;j<2;++j)
printf("%d ",v[i][j]);
puts("");
}
}*/
}I,trans,tmp,st;
Matrix fpow(Matrix a,int b)
{
Matrix res=I;
while(b)
{
if(b&1)
res=res*a;
a=a*a;
b>>=1;
}
return res;
}
int pk,pb,px,pp=-1,ls;
map<pii,int> mp;
int solve()
{
k=read(),b=read(),x0=read(),P=read();
if(k==pk && b==pb && x0==px && P==pp)
return ls;
pk=k,pb=b,px=x0,pp=P;
if(k==0)
{
if(b!=x0)
return ls=-1;
else
return ls=1;
}
trans.v[0][0]=k,trans.v[0][1]=trans.v[1][1]=1;
tmp.v[0][0]=x0,tmp.v[1][0]=b;
mp.clear();
int m=ceil(sqrt(P));
Matrix pw=I;
for(int j=0;j<m;++j)
{
st=pw*tmp;
mp[st.Hash()]=j;
pw=pw*trans;
}
Matrix tt=fpow(trans,m);
pw=tt;
for(int i=1;i*m-m+1<=P;++i)
{
st=pw*tmp;
pii val=st.Hash();
if(mp.find(val)!=mp.end())
{
int j=mp[val];
st=fpow(trans,i*m-j)*tmp;
if(st.v[0][0]==x0)
return ls=i*m-mp[val];
else
return ls=-1;
}
pw=pw*tt;
}
return ls=-1;
}
int main()
{
freopen("B.in","r",stdin);
freopen("B.out","w",stdout);
I.v[0][0]=I.v[1][1]=1;
int T=read();
while(T--)
printf("%d\n",solve());
return 0;
}
ps
以上内容均来自 \(@jklover\) 。
\(T3\)
Solution
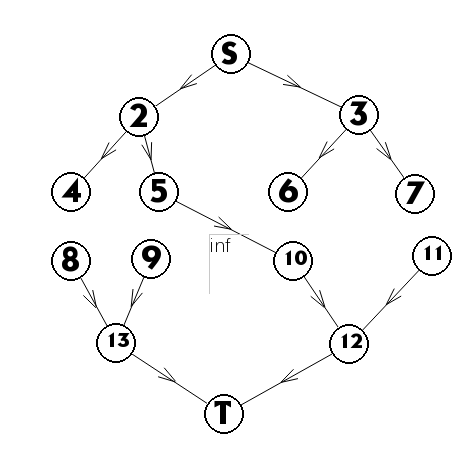
将每个数看做 \(0/1\) 串,正着建一棵字典树,反着建一棵字典树.
那么每个前缀武器就能在前缀的字典树树上割下一颗子树,每个后缀武器能的后缀的字典树上割下一颗子树.
每个给出的点在两棵树上至少被割掉一次,可以将两颗树拼在一起,建立一个最小割模型。
Code
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <queue>
#include <map>
#include <set>
#include <vector>
#include <string>
#include <stack>
#include <bitset>
#define eps 1e-8
#define FI first
#define SE second
using namespace std;
typedef long long LL;
const int MAXN = 20010;
const int MAXM = 880010;
const int INF = 0x3f3f3f3f;
struct Node
{
int from,to,next;
int cap;
}edge[MAXM];
int tol;
int head[MAXN];
int dep[MAXN];
int gap[MAXN];
int n;
void init()
{
tol=0;
memset(head,-1,sizeof(head));
}
void addedge(int u,int v,int w)
{
edge[tol].from=u;
edge[tol].to=v;
edge[tol].cap=w;
edge[tol].next=head[u];
head[u]=tol++;
edge[tol].from=v;
edge[tol].to=u;
edge[tol].cap=0;
edge[tol].next=head[v];
head[v]=tol++;
}
void BFS(int start,int end)
{
memset(dep,-1,sizeof(dep));
memset(gap,0,sizeof(gap));
gap[0]=1;
int que[MAXN];
int front,rear;
front=rear=0;
dep[end]=0;
que[rear++]=end;
while(front!=rear)
{
int u=que[front++];
if(front==MAXN)front=0;
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v=edge[i].to;
if(dep[v]!=-1)continue;
que[rear++]=v;
if(rear==MAXN)rear=0;
dep[v]=dep[u]+1;
++gap[dep[v]];
}
}
}
int SAP(int start,int end)
{
int res=0;
BFS(start,end);
int cur[MAXN];
int S[MAXN];
int top=0;
memcpy(cur,head,sizeof(head));
int u=start;
int i;
while(dep[start]<n)
{
if(u==end)
{
int temp=INF;
int inser;
for(i=0;i<top;i++)
if(temp>edge[S[i]].cap)
{
temp=edge[S[i]].cap;
inser=i;
}
for(i=0;i<top;i++)
{
edge[S[i]].cap-=temp;
edge[S[i]^1].cap+=temp;
}
res+=temp;
top=inser;
u=edge[S[top]].from;
}
if(u!=end&&gap[dep[u]-1]==0)
break;
for(i=cur[u];i!=-1;i=edge[i].next)
if(edge[i].cap!=0&&dep[u]==dep[edge[i].to]+1)
break;
if(i!=-1)
{
cur[u]=i;
S[top++]=i;
u=edge[i].to;
}
else
{
int min=n;
for(i=head[u];i!=-1;i=edge[i].next)
{
if(edge[i].cap==0)continue;
if(min>dep[edge[i].to])
{
min=dep[edge[i].to];
cur[u]=i;
}
}
--gap[dep[u]];
dep[u]=min+1;
++gap[dep[u]];
if(u!=start)u=edge[S[--top]].from;
}
}
return res;
}
int ch[MAXN][2], w[MAXN], tot;
inline int newnode() {
int x = tot++;
ch[x][0] = ch[x][1] = -1;
w[x] = INF;
return x;
}
int Insert(int p, int x) {
for(int i = 7; i >= 0; --i) {
int k = (x >> i) & 1;
if(ch[p][k] == -1) ch[p][k] = newnode();
p = ch[p][k];
}
return p;
}
void Find(int p, char *s, int v) {
for(int i = 0; s[i]; ++i) {
int k = s[i] - '0';
if(ch[p][k] == -1) return;
p = ch[p][k];
}
w[p] = min(w[p], v);
}
inline int rev(int x) {
int t = 0;
for(int i = 0; i < 8; ++i) if(x & (1 << i)) {
t |= 1 << (7 - i);
}
return t;
}
void dfs1(int u) {
for(int i = 0; i < 2; ++i) {
if(ch[u][i] == -1) continue;
addedge(u, ch[u][i], w[ch[u][i]]);
dfs1(ch[u][i]);
}
}
void dfs2(int u) {
for(int i = 0; i < 2; ++i) {
if(ch[u][i] == -1) continue;
addedge(ch[u][i], u, w[ch[u][i]]);
dfs2(ch[u][i]);
}
}
char s[MAXN];
int id1[500], id2[500];
int main() {
freopen("C.in", "r", stdin);
freopen("C.out", "w", stdout);
int N, M;
scanf("%d%d", &N, &M);
tot = 0;
int rt1 = newnode(), rt2 = newnode();
for(int x, i = 0; i < N; ++i) {
scanf("%d", &x);
id1[i] = Insert(rt1, x);
id2[i] = Insert(rt2, rev(x));
}
for(int i = 0; i < M; ++i) {
char op[2]; int w;
scanf("%s%s%d", op, s, &w);
if(strlen(s) > 8) continue;
if(*op == 'P') {
Find(rt1, s, w);
}
else {
reverse(s, s + strlen(s));
Find(rt2, s, w);
}
}
init();
for(int i = 0; i < N; ++i) {
addedge(id1[i], id2[i], INF);
}
dfs1(rt1); dfs2(rt2);
n = tot + 2;
int ans = SAP(rt1, rt2);
if(ans >= INF) ans = -1;
printf("%d\n", ans);
fclose(stdin);
fclose(stdout);
return 0;
}
ps
以上题解来自 \(@jklover\) ,程序来自某不知名的 \(std\) 。
总结
蒟蒻无语了。。。。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号