cdqz2017-test10-柚的策略（期望DP & 组合数学）

 

根据期望的可加性，我们可以算出每一位客人的期望等待时间，将他们累加

即 每一位客人所有可能情况的时间之和 / n！

设S= 每一位客人所有可能情况的时间之和

如果有f(i,p)种方案使客人i是恰好第p个进入花亭的，那对S的贡献为（n-p+1）* t[i] * f(i,p)

所以问题转变为计算f（i，p），客人i是恰好第p个进入花亭的方案数

这个恰好很难算

所以转化为在前p个进入花亭的客人中有i，最后f(i,p)减f(i,p-1)就得到了恰好是第p个

若前k+p-1个客人中至少有k-1个客人的用时比第i个客人的用时多，那么客人i可以在前p个进入花亭

所以问题又转化为了计算dp（i，j，l），在i个客人里至少有j个客人的用时比第l个客人用时多，且第i个客人一定在这i个客人里的方案数

换个状态定义会更好算：

用时相同的客人谁先进谁后进对答案没有影响

将客人的用时映射到1——n

dp（i，j，l），在1——n里选i个数至少有j个数比l大 且 不能选l的方案数

可以得到方程：（把f换成dp）

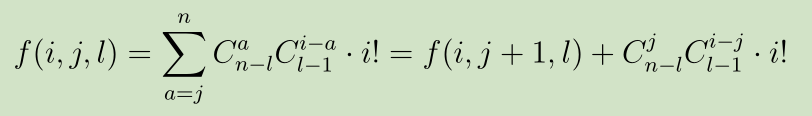
有了dp（i，j，l），再来算f（i，p）

前面说了若前k+p-1个客人中至少有k-1个客人的用时比第i个客人的用时多，那么客人i可以在前p个进入花亭

假设t[i]映射到了c

所以f（i，p）= dp[k+p-1-1][k-1][c]*(k+p-1)*(n-(k+p-1))!

因为客人i要占据一个位置，这个位置有(k+p-1)种选择，

在客人i之后的客人可以随意组合，所以是全排列

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

#define N 301 
#define M 1000001

const int mod=1e9+7;

int t[N];
int v[M],rk[N];

int C[N][N];
int fac[N];

int dp[N][N][N];
int f[N][N];

void read(int &x)
{
    x=0; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } 
}

int Pow(int a,int b)
{
    int res=1;
    for(;b;a=1LL*a*a%mod,b>>=1)
        if(b&1) res=1LL*a*res%mod;
    return res;
}

int main()
{
    freopen("strategy.in","r",stdin);
    freopen("strategy.out","w",stdout); 
    int n,k;
    read(n); read(k);
    for(int i=1;i<=n;++i) read(t[i]),v[t[i]]++;
    for(int i=1;i<M;++i) v[i]+=v[i-1];
    for(int i=1;i<=n;++i) rk[i]=v[t[i]]--;
    C[0][0]=1;
    fac[0]=1;
    for(int i=1;i<=n;++i)
    {
        C[i][0]=1;
        fac[i]=1LL*fac[i-1]*i%mod;
        for(int j=1;j<=i;++j) C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
    }
    for(int i=0;i<=n;++i)
    {
        for(int j=0;j<=i;++j)
            for(int l=1;l<=n;++l)
                dp[i][j][l]=1LL*C[n-l][j]*C[l-1][i-j]%mod*fac[i]%mod; 
        //选i个数恰好有j个数比l大的方案数
        for(int j=i;j>=0;--j) 
            for(int l=1;l<=n;++l)
            {
                dp[i][j][l]+=dp[i][j+1][l]; 
                dp[i][j][l]-=dp[i][j][l]>=mod ? mod : 0;
            }
        //选i个数至少有j个数比l大的方案数
    }
    int c,m,h; 
    int ans=0;
    for(int i=1;i<=n;++i)
    {
        c=rk[i];
        for(int j=1;j<=n;++j) // 第i个人是前j个进入花亭的 
        {
            m=min(k+j-1,n);
            h=k-1-max(0,k+j-1-n);
            f[i][j]=1LL*dp[m-1][h][c]*m%mod*fac[n-m]%mod; 
        }
        for(int j=n;j;--j)
        {
            f[i][j]-=f[i][j-1];
            if(f[i][j]<0) f[i][j]+=mod;
            ans=(ans+1LL*f[i][j]*(n-j+1)%mod*t[i]%mod)%mod;
        //    printf("%d\n",ans);
        }
    }
    ans=1LL*ans*Pow(fac[n],mod-2)%mod; 
    printf("%d",ans);
}