cdqz2017-test8-Tree(点分树)
n个点的带点权带边权的树,设点权为a[i],边权为b[i]
一棵树有n*(n-1)/2个点对,
定义这棵树的价值为任意两点对的(a[x]^a[y])*dis(x,y)
有m次修改一个点的点权的操作
输出每次修改完点权后这颗树的价值
第i次的修改会影响到第i次之后的修改
第一眼:我靠怎么又是点分树
然后因为没有处理好选的点对和自己处于根的同一子树,一下午过去了,一晚上过去了,又一个晚上过去了。。。。。。
吐槽结束,下面是题解
异或-->按位操作,点权变为1或者0,第i位的答案乘上2^i即可
点分治是每次查询跨越分治重心的点的贡献
为了支持在修改之后快速查询
我们依次查询每个点的贡献
将答案除以2就是对于初始的树的答案
对于每次的修改操作
查询出这个点的原贡献,在答案中减去
然后修改点权
再查询这个点新的贡献,再答案中加上
这样单次操作就可以log时间解决
查询的具体细节决定了点分树上要维护哪些信息
假设之前已经枚举了是第几位
假设现在查询点x对答案的贡献,x在点分树上第i层的祖先为F[x][i]
设cnt[i][0/1] 表示点分树上点i的子树内,这一位是0/1的点的个数
sum[i][0/1]表示点分树上点i的子树内,这一位是0/1的点到i的距离和
若x的这一位为t
那么x对答案的贡献分为下图中粉色和绿色的两部分
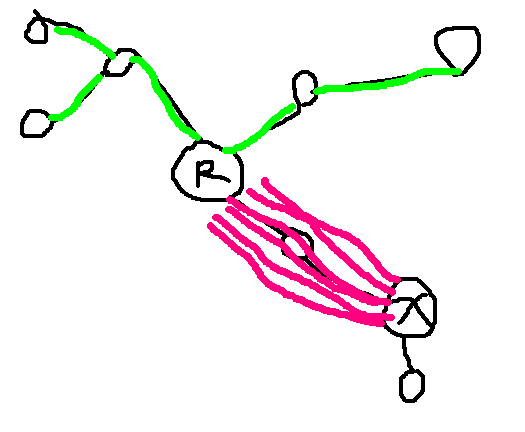
粉色部分=长度*次数== dis(x,F[x][i])*(cnt[F[x][i]][t^1] - 与x属于R的同一子树 且 这一位为t^1 的点的数量)
绿色部分=sum[F[x][i]][t^1] - 与x属于R的同一子树 且 这一位为t^1 的点到R的距离和
与x属于R的同一子树 且 这一位为t^1 的点的数量就等于cnt [ F[x][i+1] ][t^1]
设x在“原树”上R的子节点中y的子树内
与x属于R的同一子树 且 这一位为t^1 的点到R的距离和=原树上y的子树对R的贡献
所以还需要维护每一层分治重心在原树中的直接子节点对分治重心的贡献
如何记录这个?
一个点可能是多个分治重心在原树中的直接子节点
令bl[i][j]=k 表示点i属于其第j层祖先的子树kk,这个kk映射之后是k
fsum[k][0/1] 映射之后的点k对其在原树上的父节点在点分树中 的贡献
所以 与x属于R的同一子树 且 这一位为t^1 的点到R的距离和 = fsum[bl[x][i]][t^1]
学会了代码完全bfs,不用担心windows爆栈了,O(∩_∩)O哈哈~
#include<cstdio> #include<iostream> using namespace std; typedef long long LL; #define N 30001 int a[N]; int front[N],to[N<<1],nxt[N<<1],val[N<<1],tot; int F[N][16];//F[i][j]=k 点分树上点i第j层的祖先是k int D[N][16];//D[i][j]=k 点分树上点i到其第j层祖先的距离为k int dep[N];//dep[i]=j 点i处于点分树上第j层 int cnt[N][14][2];//cnt[i][j][0/1] 点分树上点i子树内点权第j位为0/1的点的数量 LL sum[N][14][2];//sum[i][j][0/1] 点分树上点i子树内点权第j位为0/1的点到点i的距离和 int bl[N][16];//bl[i][j]=k 点i属于其第j层祖先的子树kk,kk映射之后是k LL fsum[N][14][2];//fsum[i][j][0/1] 映射之后的点i对其在原树上的父节点在点分树中 的贡献 int id;//映射编号 int q[N]; int fa[N],siz[N],mx[N]; bool vis[N]; int dis[N]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } void add(int u,int v,int w) { to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; val[tot]=w; to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; val[tot]=w; } int getroot(int x) { int l=1,r=1,now; q[r++]=x; while(l<r) { now=q[l++]; siz[now]=1; mx[now]=0; for(int i=front[now];i;i=nxt[i]) if(!vis[to[i]] && to[i]!=fa[now]) { fa[to[i]]=now; q[r++]=to[i]; } } for(int i=r-1;i;--i) { siz[fa[q[i]]]+=siz[q[i]]; mx[fa[q[i]]]=max(mx[fa[q[i]]],siz[q[i]]); } for(int i=2;i<r;++i) mx[q[i]]=max(mx[q[i]],siz[q[1]]-siz[q[i]]); int big=q[1]; for(int i=2;i<r;++i) if(mx[q[i]]<mx[big]) big=q[i]; return big; } void add1(int rt,int x) { for(int i=0;i<14;++i) { cnt[rt][i][a[x]>>i&1]++; sum[rt][i][a[x]>>i&1]+=dis[x]; } } void add2(int rt,int x) { for(int i=0;i<14;++i) fsum[rt][i][a[x]>>i&1]+=dis[x]; } void bfs(int x,int d)//x为目前点分树上根节点 { int l=1,r=1,now; fa[x]=0; dis[x]=0; q[r++]=x; while(l<r) { now=q[l++]; F[now][++dep[now]]=x; D[now][dep[now]]=dis[now]; add1(x,now); for(int i=front[now];i;i=nxt[i]) if(!vis[to[i]] && to[i]!=fa[now]) { dis[to[i]]=dis[now]+val[i]; fa[to[i]]=now; q[r++]=to[i]; } } for(int i=front[x];i;i=nxt[i]) { if(vis[to[i]]) continue; l=r=1; q[r++]=to[i]; fa[q[1]]=0; id++; while(l<r) { now=q[l++]; bl[now][d]=id; add2(id,now); for(int i=front[now];i;i=nxt[i]) if(!vis[to[i]] && to[i]!=fa[now]) { fa[to[i]]=now; q[r++]=to[i]; } } } } void build(int x,int d) { int big=getroot(x); // printf("第%d层分治重心是%d\n",d,big); vis[big]=true; bfs(big,d); for(int i=front[big];i;i=nxt[i]) if(!vis[to[i]]) build(to[i],d+1); } LL query(int x) { LL ans=0; int t; // int aa,bb,cc; for(int i=1;i<dep[x];++i) for(int j=0;j<14;++j) { t=a[x]>>j&1; ans+=1LL*(cnt[F[x][i]][j][t^1]-cnt[F[x][i+1]][j][t^1])*D[x][i]+(sum[F[x][i]][j][t^1]-fsum[bl[x][i]][j][t^1])<<j; // aa=(cnt[F[x][i]][j][t^1]-cnt[F[x][i+1]][j][t^1])*D[x][i]; // bb=sum[F[x][i]][j][t^1]; // cc=fsum[bl[x][i]][j][t^1]; } for(int j=0;j<14;++j) { t=a[x]>>j&1; ans+=1LL*sum[x][j][t^1]<<j; } return ans; } void change(int x,int y) { int t; for(int j=0;j<14;++j) { if((a[x]>>j&1)==(y>>j&1)) continue; t=a[x]>>j&1; for(int i=1;i<=dep[x];++i) { cnt[F[x][i]][j][t]--; sum[F[x][i]][j][t]-=D[x][i]; cnt[F[x][i]][j][t^1]++; sum[F[x][i]][j][t^1]+=D[x][i]; if(i<dep[x]) { fsum[bl[x][i]][j][t]-=D[x][i]; fsum[bl[x][i]][j][t^1]+=D[x][i]; } } } a[x]=y; } void out(LL x) { if(x>9) out(x/10); putchar(x%10+'0'); } int main() { //freopen("data.in","r",stdin); //freopen("tree.out","w",stdout); int n,m; read(n); for(int i=1;i<=n;++i) read(a[i]); int u,v,w; for(int i=1;i<n;++i) { read(u); read(v); read(w); add(u,v,w); } build(1,1); LL ans=0; for(int i=1;i<=n;++i) { ans+=query(i); // cout<<i<<' '<<query(i)<<'\n'; } ans>>=1; // cout<<ans<<'\n'; /* for(int i=1;i<=n;++i) { for(int j=1;j<dep[i];++j) printf("%d ",bl[i][j]); printf("\n"); }*/ read(m); while(m--) { read(u); read(v); ans-=query(u); change(u,v); ans+=query(u); out(ans); putchar('\n'); } // printf("%d",id); }