bzoj千题计划281：bzoj4558: [JLoi2016]方

http://www.lydsy.com/JudgeOnline/problem.php?id=4558

 

容斥原理

全部的正方形-至少有一个点被删掉的+至少有两个点被删掉的-至少有3个点被删掉的+至少有4个点被删掉的

 

正方形分 正着的和斜着的

斜着的正方形卡在一个正着的正方形的边框上

一个边长为i的正方形框，恰好可以框住i个正方形（1个正着的 和 i-1个斜着的）

 

所以 总的正方形=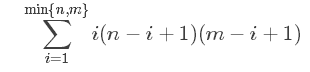 

 

至少有一个点被删掉的：

枚举一个被删掉的点，

设它的上边有u行，下边有d行，左边有l列，右边有r列

那么以一对相对的边为底边，在确定一边作为高，就可以计算这个方向上的 贡献

比如 以l和r 为 底边（向左可以延伸l，向右可以延伸r），以u为高（向上可以延伸u）

一个边长为a的正方形框 可以唯一包含一个 有一个顶点 在正方形框上的正方形

正方形框 长为1的有2种，长为2的有3种，长为a的有a+1种

所以，如果最大的正方形框 长为z，

那么用等差数列求和公式可得， 这种情况下总的正方形数 为 z*（z+3）/2 

z=min（h，l+r）

但是有一个问题

若z>l，那么 当正方形框为a（a>l）的时候，

 正方形左边有一部分要出界，

一共有z-l 种 边长在左边要出界，由等差数列求和公式，这种情况下总的正方形数 还要减去  (z-l)*(z-l+1)/2

z>r 同理，还要减去 (z-r)*(z-r+1)/2

 

至少有两个点被删掉的：

枚举任意两个点p，q

设向量v=（q.x-p.x ，q.y-p.y）

如果正方形是正着的，那么这两个点在正方形的同一条边上

将向量v顺时针旋转90°，再将两个点平移向量v，即可得到一个正方形的另外两个点

判断这两个点是否出界，没有出界的话，贡献加1

同理，将向量v逆时针旋转90°，再将两个点平移，即可得到另一个方向的正方形

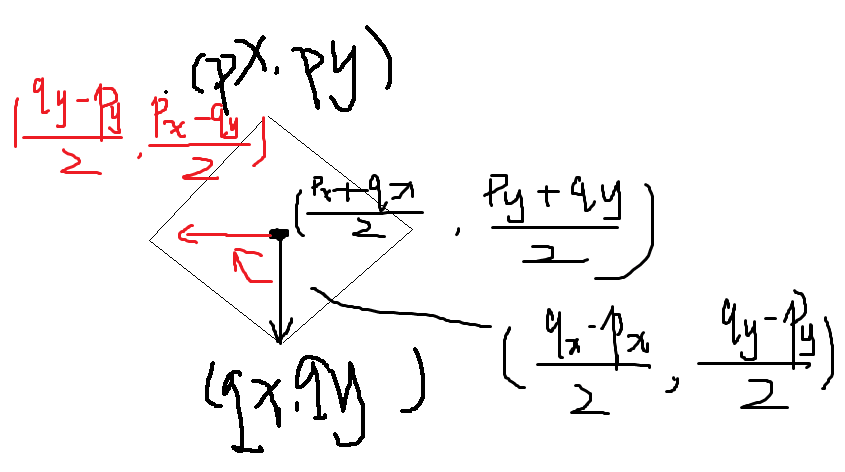
如果正方形是斜着的，那么枚举的这两个点当做对角线

假设两个点（px，py），（qx，qy）是正方形对角线上的两个顶点。
令dx=px-qx，dy=py-qy，x=（dx-dy）/2，y=（dx+dy）/2
那么 正方形的另一条对角线上的 两个顶点 分别为（px-x，py-y）和（qx+x，qy+y）

这个的求解，算出正方形的中心坐标，然后向量旋转，加加减减，就可以得到这个。。。

 

 

至少有3/4个点被删掉的：

在计算至少有两个点被删掉的时候，判断的时候 顺带 判上

 

然后计算至少被删3个点的，每个正方形计算了C（3,2）=3 遍

至少被删4个点的，每个正方形计算了C（4,2）=6 遍

再除一下

#include<set>
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;

const int mod=1e8+7;

int n,m;

struct Point
{
    int x,y;
    
    bool operator < (Point p) const
    {
        return x<p.x || x==p.x&&y<p.y;
    }
    
    Point(int x_=0,int y_=0):x(x_),y(y_){}
}e[2001];

set<Point>mp;

void read(int &x)
{
    x=0; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); }
}

int cal(int l,int r,int h)
{
    int z=min(l+r,h);
    long long ans=1LL*z*(z+3)/2;
    if(z>l) ans-=1LL*(z-l)*(z-l+1)/2;
    if(z>r) ans-=1LL*(z-r)*(z-r+1)/2;
    return ans%mod;
}

int One(int x,int y)
{
    int u=x,d=n-x,l=y,r=m-y;
    return cal(u,d,l)+cal(u,d,r)+cal(l,r,u)+cal(l,r,d)-min(u,l)-min(l,d)-min(d,r)-min(r,u);
}

bool inmap(Point p)
{
    return p.x>=0 && p.x<=n && p.y>=0 && p.y<=m ;
}

int count(Point p,Point q,int &cnt2,int &cnt3,int &cnt4)
{
    if(inmap(p) && inmap(q))
    {
        int t=mp.count(p)+mp.count(q);
        cnt2++;
        if(t) cnt3++;
        if(t>1) cnt3++,cnt4++;
    }
}

int main()
{
    int k;
    read(n); read(m); read(k);
    int ans=0; int t=min(n,m);
    for(int i=1;i<=t;++i) ans=(ans+1LL*i*(n-i+1)%mod*(m-i+1)%mod)%mod;
    int x,y;
    for(int i=1;i<=k;++i)
    {
        read(x); read(y);
        mp.insert(Point(x,y));
        e[i]=Point(x,y);
        (ans-=One(x,y))%=mod;
    }
    Point p,q;
    int cnt2=0,cnt3=0,cnt4=0;
    int dx,dy;
    for(int i=1;i<=k;++i)
    {
        p=e[i];
        for(int j=i+1;j<=k;++j)
        {
            q=e[j];
            dx=p.x-q.x; dy=p.y-q.y;
            count(Point(p.x+dy,p.y-dx),Point(q.x+dy,q.y-dx),cnt2,cnt3,cnt4);
            count(Point(p.x-dy,p.y+dx),Point(q.x-dy,q.y+dx),cnt2,cnt3,cnt4);
            if(abs(dx)+abs(dy) & 1) continue;
            x=dx-dy>>1; y=dx+dy>>1;
            count(Point(p.x-x,p.y-y),Point(q.x+x,q.y+y),cnt2,cnt3,cnt4);
        }
    }
    ans+=cnt2-cnt3/3+cnt4/6;
    ans%=mod;
    if(ans<0) ans+=mod;
    printf("%d",ans);
}