bzoj千题计划270:bzoj4559: [JLoi2016]成绩比较(拉格朗日插值)
http://www.lydsy.com/JudgeOnline/problem.php?id=4559
f[i][j] 表示前i门课,有j个人没有被碾压的方案数
g[i] 表示第i门课,满足B神排名的分数安排方案数
g[i]的求法:
枚举B神这门课x分,则有n-Ri个人的分数<=x ,Ri-1个人的分数>x
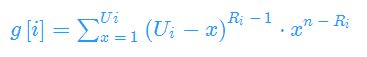
Ui 上限是1e9,但是g[i] 是一个关于Ui 的n次多项式,所以可以用拉格朗日插值法来求
递推 f[i][j]:
假设f[i-1][w] 转移到了f[i][j],j>=w
前i-1门课没有被碾压,前i门课也一定没有被碾压
前i-1门课被碾压,前i门课可能继续被碾压,也可能不再被碾压
单看这一门课有Ri-1个人的成绩比B神高
但这Ri-1个人之前可能就有科目比B神高,已经不被碾压,这次成绩比B神高还是低都行
所以实际新增加了j-w个没有被碾压的,即这j-w个人 这一门 的成绩比B神高,之前的科目都比B神低
在已经没有被碾压的w个人中,还存在 Ri-1-(j-w) 个人的成绩比B神高
之前有n-w-1个人被碾压,所以新增情况的方案数为C(n-w-1,j-w)
后一种情况的方案数为C(w,Ri-1-j+w)
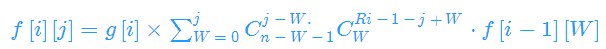
#include<cstdio> #include <iostream> using namespace std; const int mod=1e9+7; #define N 101 int C[N][N]; int U[N],rk[N]; int f[N][N]; int g[N]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } int get_C(int n,int m) { if(n<0 || m<0 || n<m) return 0; return C[n][m]; } void pre_C() { C[0][0]=1; for(int i=1;i<=100;++i) { C[i][0]=1; for(int j=1;j<=i;++j) C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod; } } int Pow(int a,int b) { int res=1; for(;b;a=1LL*a*a%mod,b>>=1) if(b&1) res=1LL*res*a%mod; return res; } int Langrange(int n,int r,int k) { for(int u=1;u<=k;++u) { g[u]=0; for(int x=1;x<=u;++x) g[u]=(g[u]+1LL*Pow(u-x,r-1)*Pow(x,k-1-r)%mod)%mod; if(n==u) return g[u]; } int fz=1; for(int i=1;i<=k;++i) fz=1LL*fz*(n-i)%mod; int fm,ans=0; for(int i=1;i<=k;++i) { fm=n-i; for(int j=1;j<=k;++j) if(i!=j) fm=1LL*fm*(i-j)%mod; ans=(ans+1LL*fz*g[i]%mod*Pow(fm,mod-2)%mod)%mod; } if(ans<0) ans+=mod; return ans; } int main() { int n,m,k; read(n); read(m); read(k); for(int i=1;i<=m;++i) read(U[i]); for(int i=1;i<=m;++i) read(rk[i]); pre_C(); int G; f[0][0]=1; for(int i=1;i<=m;++i) { G=Langrange(U[i],rk[i],n+1); for(int j=0;j<=n;++j) { for(int w=0;w<=j;++w) f[i][j]=(f[i][j]+1LL*f[i-1][w]*get_C(w,rk[i]-1-j+w)%mod*get_C(n-w-1,j-w)%mod)%mod; f[i][j]=1LL*f[i][j]*G%mod; } } printf("%d",f[m][n-k-1]); return 0; }
4559: [JLoi2016]成绩比较
Time Limit: 20 Sec Memory Limit: 256 MBSubmit: 366 Solved: 211
[Submit][Status][Discuss]
Description
G系共有n位同学,M门必修课。这N位同学的编号为0到N-1的整数,其中B神的编号为0号。这M门必修课编号为0到M-
1的整数。一位同学在必修课上可以获得的分数是1到Ui中的一个整数。如果在每门课上A获得的成绩均小于等于B获
得的成绩,则称A被B碾压。在B神的说法中,G系共有K位同学被他碾压(不包括他自己),而其他N-K-1位同学则没
有被他碾压。D神查到了B神每门必修课的排名。这里的排名是指:如果B神某门课的排名为R,则表示有且仅有R-1
位同学这门课的分数大于B神的分数,有且仅有N-R位同学这门课的分数小于等于B神(不包括他自己)。我们需要
求出全系所有同学每门必修课得分的情况数,使其既能满足B神的说法,也能符合D神查到的排名。这里两种情况不
同当且仅当有任意一位同学在任意一门课上获得的分数不同。你不需要像D神那么厉害,你只需要计算出情况数模1
0^9+7的余数就可以了。
Input
第一行包含三个正整数N,M,K,分别表示G系的同学数量(包括B神),必修课的数量和被B神碾压的同学数量。第二
行包含M个正整数,依次表示每门课的最高分Ui。第三行包含M个正整数,依次表示B神在每门课上的排名Ri。保证1
≤Ri≤N。数据保证至少有1种情况使得B神说的话成立。N<=100,M<=100,Ui<=10^9
Output
仅一行一个正整数,表示满足条件的情况数模10^9+7的余数。
Sample Input
3 2 1
2 2
1 2
2 2
1 2
Sample Output
10


