Codeforces 932 E. Team Work（组合数学）

http://codeforces.com/contest/932/problem/E

 

题意：

 

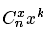  可以看做 有n种小球，每种小球有无限个，先从中选出x种，再在这x种小球中任选k个小球的方案数

选出的x种不一样，任选k个球的顺序不一样 均视做不同的方案

f[i][j] 表示选了i个小球，来自j种的方案数

那么答案就是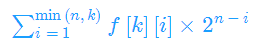

考虑选的第i个球是否是选过的一种，

f[i][j]=f[i-1][j]*j+f[i-1][j-1]*(n-(j-1))

#include<cstdio>
#include<algorithm>

using namespace std;

const int mod=1e9+7;

int f[5001][5001];

int Pow(int a,int b)
{
    int res=1;
    for(;b;a=1LL*a*a%mod,b>>=1)
        if(b&1) res=1LL*res*a%mod;
    return res;
}

int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    f[0][0]=1;
    for(int i=1;i<=k;++i) 
        for(int j=1;j<=i;++j)
            f[i][j]=(1LL*f[i-1][j]*j%mod+1LL*f[i-1][j-1]*(n-j+1)%mod)%mod;
    int ans=0;
    int m=min(n,k);
    for(int i=1;i<=m;++i) ans=(ans+1LL*f[k][i]*Pow(2,n-i)%mod)%mod;
    printf("%d",ans);
}