bzoj千题计划263:bzoj4870: [六省联考2017]组合数问题
http://www.lydsy.com/JudgeOnline/problem.php?id=4870

80分暴力打的好爽 \(^o^)/~
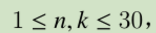
预处理杨辉三角

令m=n*k
要求满足m&x==x ,x<=m, x%k==r 的x的个数
结论:若n&m==m,则C(n,m)为奇数,否则为偶数
枚举m的子集,判断是否%k==r
时间复杂度:O(m的位子集个数),即O(2^(m的二进制中1的个数))极限是O(n*k)

杨辉三角第i行的和=2^i,即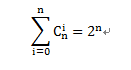
那么用2^(nk) 减去 前面不用的C
因为r<=50,所以这种C的个数<=50
暴力计算C即可
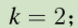
k=2 就是C(2n,r)+C(2n,r+2)+C(2n,r+4)……
是隔一个加一个
杨辉三角 每一行的 奇数列之和=偶数列之和
所以 2^(2n)/2 - 前面不用的C,也是隔一个减一个
除2的计算 要乘2的逆元,但是p不是素数
所以 计算2^(2n) 改成计算 2^(2n-1)
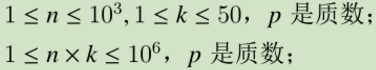
预处理阶乘和阶乘的逆元,枚举计算C ,最多会计算n个C
不会,求指点
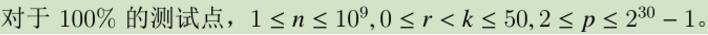
考虑组合数C(n,m)的实际意义:从n个元素里选出m个元素的方案数
那么本题就是求从n*k个元素里,选出%k=r个元素的方案数
dp[i][j] 表示从前i个元素里,选出%k=j 个元素的方案数
第i个不选:dp[i][j]+=dp[i-1][j]
第i个选:dp[i][j]+=dp[i-1][(j-1+k)%k]
矩阵乘法优化

#include<cstdio> #include<cstring> using namespace std; int p,K; int a[50][50],ans[50][50],f[50][50]; int C[50][50]; void mul(int A[50][50],int B[50][50]) { memset(C,0,sizeof(C)); for(int i=0;i<K;++i) for(int j=0;j<K;++j) for(int k=0;k<K;++k) C[i][j]=(C[i][j]+1LL*A[i][k]*B[k][j]%p)%p; for(int i=0;i<K;++i) for(int j=0;j<K;++j) A[i][j]=C[i][j]; } int main() { int n,k,r; scanf("%d%d%d%d",&n,&p,&K,&r); for(int i=0;i<=K-2;++i) a[i][i]=a[i][i+1]=1; a[K-1][K-1]++; a[K-1][0]++; f[0][0]=1; for(int i=0;i<K;++i) ans[i][i]=1; long long m=1LL*n*K; for(;m;mul(a,a),m>>=1) if(m&1) mul(ans,a); mul(f,ans); printf("%d",f[0][r]); }

#include<cstdio> #include<cstring> using namespace std; typedef long long LL; int n,p,k,r; int C[901][901]; int num[51]; int inv[1000001],fac[1000001]; LL xx; void ADD(int &x,int y) { xx=x; xx+=y; xx-=xx>=p ? p : 0; x=xx; } void YangHui() { C[0][0]=1; int m=n*k; for(int i=1;i<=m;++i) { C[i][0]=1; for(int j=1;j<=m;++j) C[i][j]=(1LL*C[i-1][j]+C[i-1][j-1])%p; } int ans=0; for(int i=0;i<=n;++i) { if(i*k+r>m) break; ADD(ans,C[m][i*k+r]); } printf("%d",ans); } void Yu() { LL m=1LL*n*k; int ans=0; for(LL t=m;t;t=(t-1)&m) if(t%k==r) ans^=1; printf("%d",ans); } int Pow(int a,int b) { int res=1; for(;b;a=1LL*a*a%p,b>>=1) if(b&1) res=1LL*res*a%p; return res; } int get_gcd(int a,int b) { return !b ? a : get_gcd(b,a%b); } int get_C(int m,int k) { for(int i=m-k+1;i<=m;++i) num[i]=i; int x,gcd; for(int i=2;i<=k;++i) { x=i; for(int j=m-k+1;j<=m && x!=1;++j) { gcd=get_gcd(num[j],x); num[j]/=gcd; x/=gcd; } } int ans=1; for(int i=m-k+1;i<=m;++i) ans=1LL*ans*num[i]; return ans; } void PreSum() { int a=Pow(2,n); int b=0; for(int i=0;i<r;++i) ADD(b,get_C(n,i)); a-=b; if(a<0) a+=p; printf("%d",a); } void JiOu() { int a=Pow(2,n*2-1); int b=0; for(int i=r-2;i>=0;i-=2) ADD(b,get_C(n<<1,i)); a-=b; if(a<0) a+=b; printf("%d",a); } int get_inv(int x) { if(inv[x]!=-1) return inv[x]; inv[x]=Pow(fac[x],p-2); return inv[x]; } void Cal() { int m=n*k; fac[0]=1; for(int i=1;i<=m;++i) fac[i]=1LL*fac[i-1]*i%p; memset(inv,-1,sizeof(inv)); inv[0]=1; int h=r; int ans=0; int tmp; for(int i=1; h<=m;++i,h+=k) { tmp=fac[m]; tmp=1LL*tmp*get_inv(h)%p*get_inv(m-h)%p; ADD(ans,tmp); } printf("%d",ans); } int main() { freopen("problem.in","r",stdin); freopen("problem.out","w",stdout); scanf("%d%d%d%d",&n,&p,&k,&r); if(n<=30 && k<=30) YangHui(); else if(p==2) Yu(); else if(k==1) PreSum(); else if(k==2) JiOu(); else Cal(); return 0; }
脑抽错误:
C(n,m)一定是偶数,但 对p 取模之后不能保证是偶数
考试的时候没考虑这个 ,直接/2 丢了10分,~~~~(>_<)~~~~




 浙公网安备 33010602011771号
浙公网安备 33010602011771号