扩展BSGS算法

求解A^x ≡ B mod P （P不一定是质数）的最小非负正整数解

 

先放几个同余定理：

 

 

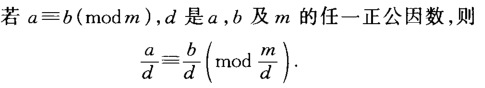
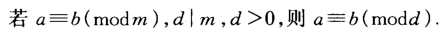
一、判断如果B==1，那么x=0，算法结束

二、若gcd（A，P）不能整除 B，则 无解，算法结束

三、若gcd（A，P）！=1，令d=gcd（A，P），若d不能整除B，则无解，算法结束。

有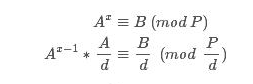

四、持续步骤三，直至 gcd（A，）=1

有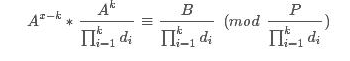 

五、枚举 0<x<k，若有解，输出x，算法结束

六、对于x>=k，

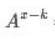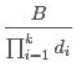A=，B=，P=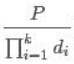

A，P 互素 ，

直接用BSGS 求    * A ^ x ≡ B mod P

所得结果再+k即可

 

#include<map>
#include<cmath>
#include<cstdio>
#include<iostream> 
#include<algorithm> 
 
using namespace std;

typedef long long LL;
 
map<int,int>mp;

void read(int &x)
{
    x=0; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); }
}
 
int get_gcd(int a,int b) { return !b ? a : get_gcd(b,a%b); }
 
int Pow(int a,int b,int mod)
{
    int res=1;
    for(;b;a=1LL*a*a%mod,b>>=1)
        if(b&1) res=1LL*res*a%mod;
    return res;
}   
 
int ex_BSGS(int A,int B,int C)
{
    if(B==1) return 0;
    int k=0,tmp=1,d;
    while(1)
    {
        d=get_gcd(A,C);
        if(d==1) break;
        if(B%d) return -1;
        B/=d; C/=d;
        tmp=1LL*tmp*(A/d)%C;
        k++;
        if(tmp==B) return k;
    }
    mp.clear();
    int mul=B;
    mp[B]=0;
    int m=ceil(sqrt(1.0*C));
    for(int j=1;j<=m;++j) 
    {
        mul=1LL*mul*A%C;
        mp[mul]=j;
    }
    int am=Pow(A,m,C);
    mul=tmp;
    for(int j=1;j<=m;++j)
    {
        mul=1LL*mul*am%C;
        if(mp.count(mul)) return j*m-mp[mul]+k;
    }
    return -1;
}
 
int main()
{
    int A,C,B;
    int ans;
    while(1)
    {
        read(A); read(B); read(C); 
        if(!A) return 0;
        ans=ex_BSGS(A,B,C);
        if(ans==-1) puts("No Solution");
        else cout<<ans<<'\n';
    }
}