bzoj3730: 震波(点分树)
http://www.lydsy.com/JudgeOnline/problem.php?id=3730
点分树内对每个节点动态维护2颗线段树
线段树以距离为下标,城市的价值为权值
对于节点x的两棵线段树:
一棵维护 点分树中,x的子树 的贡献
一棵维护 点分树中,x对x的父节点的贡献
查询和修改时,暴力往上爬点分树
点分树保证了最多往上爬log次
查询x k时,先加上点分树内,x的子树中距离<=k的权值和,
再爬到x的父节点f,若x和f的距离为d,则加上f的子树中距离<=k-d的权值和,还要减去 x对f 贡献的<=k-d的权值和,因为这一部分在之前x的子树中算过了
以此类推 ,这就是第二棵线段树的作用
常数优化:
原代码总耗时:20.105 s

#include<cstdio> #include<iostream> #include<algorithm> using namespace std; #define N 100001 int n,a[N]; int front[N],nxt[N<<1],to[N<<1],tot; int all,root; int siz[N],f[N]; bool vis[N]; int dep[N]; int fa[N][18],dis[N][18]; struct Segment { int cnt; int rt[N]; int lc[N*80],rc[N*80],val[N*80]; void Change(int &k,int l,int r,int x,int y) { if(!k) k=++cnt; if(l==r) { val[k]+=y; return; } int mid=l+r>>1; if(x<=mid) Change(lc[k],l,mid,x,y); else Change(rc[k],mid+1,r,x,y); val[k]=val[lc[k]]+val[rc[k]]; } int Query(int k,int l,int r,int x) { if(!k) return 0; if(r<=x) return val[k]; int mid=l+r>>1; if(x<=mid) return Query(lc[k],l,mid,x); else return val[lc[k]]+Query(rc[k],mid+1,r,x); } }tr,ftr; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } void add(int u,int v) { to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; } void getroot(int x,int y) { siz[x]=1; f[x]=0; for(int i=front[x];i;i=nxt[i]) if(to[i]!=y && !vis[to[i]]) { getroot(to[i],x); siz[x]+=siz[to[i]]; f[x]=max(f[x],siz[to[i]]); } f[x]=max(f[x],all-siz[x]); if(f[x]<f[root]) root=x; } void cal(int x,int ancestor,int father,int d) { int t; for(int i=front[x];i;i=nxt[i]) { t=to[i]; if(t!=father && !vis[t]) { fa[t][++dep[t]]=ancestor; dis[t][dep[t]]=d+1; cal(t,ancestor,x,d+1); } } } void build(int x) { vis[x]=true; cal(x,x,0,0); int tmp=all; for(int i=front[x];i;i=nxt[i]) if(!vis[to[i]]) { all=siz[to[i]]; if(all>siz[x]) all=tmp-siz[x]; root=0; getroot(to[i],0); build(root); } } void change(int x,int y) { tr.Change(tr.rt[x],0,n-1,0,y); int d; for(int i=dep[x];i;--i) { ftr.Change(ftr.rt[fa[x][i+1]],0,n-1,dis[x][i],y); // printf("kk %d\n",dis[x][i]); tr.Change(tr.rt[fa[x][i]],0,n-1,dis[x][i],y); } } int query(int x,int d) { int ans=tr.Query(tr.rt[x],0,n-1,d); for(int i=dep[x];i;--i) { if(d-dis[x][i]>=0) ans+=tr.Query(tr.rt[fa[x][i]],0,n-1,d-dis[x][i]); if(d-dis[x][i]>=0) ans-=ftr.Query(ftr.rt[fa[x][i+1]],0,n-1,d-dis[x][i]); } return ans; } void out(int x) { if(x>=10) out(x/10); putchar(x%10+'0'); } int main() { freopen("wave.in","r",stdin); freopen("wave.out","w",stdout); int size = 256 << 20; // 256MB char *p = (char*)malloc(size) + size; __asm__("movl %0, %%esp\n" :: "r"(p)); int m; read(n); read(m); for(int i=1;i<=n;++i) read(a[i]); int u,v; for(int i=1;i<n;++i) { read(u); read(v); add(u,v); } f[0]=n+1; all=n; getroot(1,0); build(root); for(int i=1;i<=n;++i) fa[i][dep[i]+1]=i; for(int i=1;i<=n;++i) change(i,a[i]); int ty,last=0; while(m--) { read(ty); read(u); read(v); u^=last; v^=last; if(!ty) last=query(u,v),out(last),printf("\n"); else change(u,v-a[u]),a[u]=v; } //printf("%d %d",tr.cnt,ftr.cnt); return 0; }
1、原本线段树的操作封装在结构体里,拿出来,总耗时:16.934 s
2、动态开节点线段树 单点加:
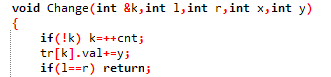
在寻找x的路径上就进行加操作,而不是找到后再update
总耗时:14.357 s
3、数组改成结构体 总耗时:12.684 s
#include<cstdio> #include<iostream> #include<algorithm> using namespace std; #define N 100001 int n,a[N]; int front[N],nxt[N<<1],to[N<<1],tot; int all,root; int siz[N],f[N]; bool vis[N]; int dep[N]; int fa[N][18],dis[N][18]; int rt[N<<1],cnt; struct node { int lc,rc,val; }tr[N*150]; void Change(int &k,int l,int r,int x,int y) { if(!k) k=++cnt; tr[k].val+=y; if(l==r) return; int mid=l+r>>1; if(x<=mid) Change(tr[k].lc,l,mid,x,y); else Change(tr[k].rc,mid+1,r,x,y); } int Query(int k,int l,int r,int x) { if(!k) return 0; if(r<=x) return tr[k].val; int mid=l+r>>1; if(x<=mid) return Query(tr[k].lc,l,mid,x); else return tr[tr[k].lc].val+Query(tr[k].rc,mid+1,r,x); } void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } void add(int u,int v) { to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; } void getroot(int x,int y) { siz[x]=1; f[x]=0; for(int i=front[x];i;i=nxt[i]) if(to[i]!=y && !vis[to[i]]) { getroot(to[i],x); siz[x]+=siz[to[i]]; f[x]=max(f[x],siz[to[i]]); } f[x]=max(f[x],all-siz[x]); if(f[x]<f[root]) root=x; } void cal(int x,int ancestor,int father,int d) { int t; for(int i=front[x];i;i=nxt[i]) { t=to[i]; if(t!=father && !vis[t]) { fa[t][++dep[t]]=ancestor; dis[t][dep[t]]=d+1; cal(t,ancestor,x,d+1); } } } void build(int x) { vis[x]=true; cal(x,x,0,0); int tmp=all; for(int i=front[x];i;i=nxt[i]) if(!vis[to[i]]) { all=siz[to[i]]; if(all>siz[x]) all=tmp-siz[x]; root=0; getroot(to[i],0); build(root); } } void change(int x,int y) { Change(rt[x],0,n-1,0,y); int d; for(int i=dep[x];i;--i) { Change(rt[fa[x][i+1]+n],0,n-1,dis[x][i],y); // printf("kk %d\n",dis[x][i]); Change(rt[fa[x][i]],0,n-1,dis[x][i],y); } } int query(int x,int d) { int ans=Query(rt[x],0,n-1,d); for(int i=dep[x];i;--i) { if(d-dis[x][i]>=0) ans+=Query(rt[fa[x][i]],0,n-1,d-dis[x][i]); if(d-dis[x][i]>=0) ans-=Query(rt[fa[x][i+1]+n],0,n-1,d-dis[x][i]); } return ans; } void out(int x) { if(x>=10) out(x/10); putchar(x%10+'0'); } int main() { int m; read(n); read(m); for(int i=1;i<=n;++i) read(a[i]); int u,v; for(int i=1;i<n;++i) { read(u); read(v); add(u,v); } f[0]=n+1; all=n; getroot(1,0); build(root); for(int i=1;i<=n;++i) fa[i][dep[i]+1]=i; for(int i=1;i<=n;++i) change(i,a[i]); int ty,last=0; while(m--) { read(ty); read(u); read(v); u^=last; v^=last; if(!ty) last=query(u,v),out(last),printf("\n"); else change(u,v-a[u]),a[u]=v; } //printf("%d %d",tr.cnt,ftr.cnt); return 0; }



