hdu 5079 Square

http://acm.hdu.edu.cn/showproblem.php?pid=5079

 

题意：

n*n网格，每个格子可以涂黑色或白色，有的格子必须涂黑色

问最大白色正方形边长分别为0,1,2，……n 的涂色方案数

 

令ans[i]表示最大白色正方形边长小于i的方案数

最大边长=i 的就是ans[i+1]-ans[i]

枚举sz，表示现在要求最大白色正方形边长<i的方案数

设dp[i][st] 表示前i行，状态为st的方案数

st内压缩了n-sz+1个数，其中的第j个数表示 从右往左数第j列，第j+1列，…… 第j+sz-1列 中，自第i行向上延伸的连续白色正方形数量的 最小值

要st中的每个数<sz，>=sz 就不是要求的最大边长<i

转移：

先枚举求到了第i行，枚举上一行的状态st

枚举本行有哪些格子要涂成白色，假设st的第j个数为f[j]

那么 如果本行从右往左数 第j列，第j+1列……第j+sz-1列 都涂了白色，new_f[j]=f[j]+1

只要有一个不是白色，那new_f[j]=0

new_f[j]压缩成 要转移到的状态 new_st

dp[i][new_st]+=dp[i-1][st]

所有的dp[n][] 累积就是ans[sz]

 

#include<cmath>
#include<cstdio>
#include<cstring>

using namespace std;

const int mod=1e9+7;

char s[9];
int broken[9];

int bit[9];

int f[9][1027];
int ans[10];

int main()
{
    int T;
    scanf("%d",&T);
    int n,m;
    int tot;
    while(T--)
    {
        scanf("%d",&n);
        tot=1;
        for(int i=1;i<=n;++i)
        {
            scanf("%s",s+1);
            broken[i]=0;
            for(int j=1;j<=n;++j)
                if(s[j]=='*') broken[i]|=1<<j-1;
                else tot<<=1,tot-=tot>=mod ? mod : 0;
        }
        ans[1]=1; ans[n+1]=tot;
        for(int sz=2;sz<=n;++sz)
        {
            memset(f,0,sizeof(f));
            f[0][0]=1;
            bit[0]=1;
            for(int i=1;i<n;++i) bit[i]=bit[i-1]*sz;
            m=0;
            for(int i=1;i+sz-1<=n;++i) m=m*sz+sz-1;
            for(int i=1;i<=n;++i)
                for(int st=0;st<=m;++st)
                    if(f[i-1][st])
                        for(int j=0;j<1<<n;++j)
                            if(!(broken[i]&j))
                            {
                                int nxt=0;
                                for(int tmp=j,l=1;l+sz-1<=n;++l,tmp>>=1)
                                {
                                    int now=(tmp&((1<<sz)-1))==((1<<sz)-1) ? st/bit[l-1]%sz+1 : 0;
                                    if(now>=sz) { nxt=-1; break; }
                                    nxt+=now*bit[l-1];
                                }
                                if(nxt!=-1)
                                {
                                    f[i][nxt]+=f[i-1][st];
                                    f[i][nxt]-=f[i][nxt]>=mod ? mod : 0;
                                }
                            }
            ans[sz]=0;
            for(int st=0;st<=m;++st) 
            {
                ans[sz]+=f[n][st];
                ans[sz]-=ans[sz]>=mod ? mod : 0;
            }
        }
        for(int i=0;i<=n;++i) printf("%d\n",(ans[i+1]-ans[i]+mod)%mod);
    }
    return 0;
}

 

Square

Time Limit: 24000/12000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 307    Accepted Submission(s): 207

Problem Description

Nothing is more beautiful than square! So, given a grid of cells, each cell being black or white, it is reasonable to evaluate this grid’s beautifulness by the side length of its maximum continuous subsquare which fully consists of white cells.

Now you’re given an N × N grid, and the cells are all black. You can paint some cells white. But other cells are broken in the sense that they cannot be paint white. For each integer i between 0 and N inclusive, you want to find the number of different painting schemes such that the beautifulness is exactly i. Two painting schemes are considered different if and only if some cells have different colors. Painting nothing is considered to be a scheme.


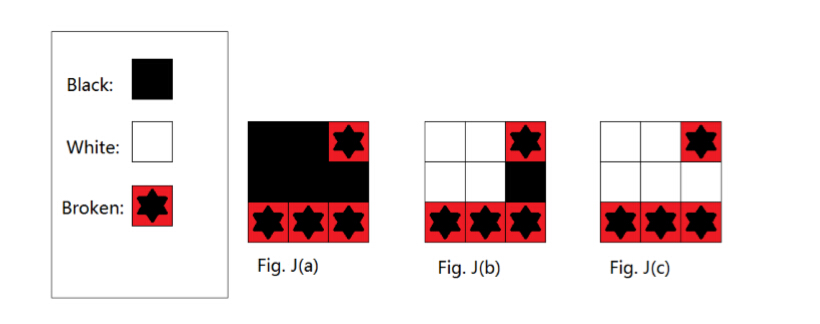
For example, N = 3 and there are 4 broken cells as shouwn in Fig. J(a). There are 2 painting schemes for i=2 as shown in Fig. J(b) and J(c).

You just need to output the answer modulo 10⁹ + 7.

 

 

Input

The first line contains an integer T (T ≤ 10) denoting the number of the test cases.

For each test case, the first line contains an integer N (1 ≤ N ≤ 8), denoting the size of the grid is N × N . Then N lines follow, each line containing an N-character string of “o” and “*”, where “o” stands for a paintable cell and “*” for a broken cell.

 

 

Output

For each test case, for each integer i between 0 and N inclusive, output the answer in a single line.

 

 

Sample Input

2 3 oo* ooo *** 8 oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo oooooooo

 

 

Sample Output

1 29 2 0 1 401415247 525424814 78647876 661184312 550223786 365317939 130046 1