bzoj千题计划230:bzoj3205: [Apio2013]机器人
http://www.lydsy.com/JudgeOnline/problem.php?id=3205
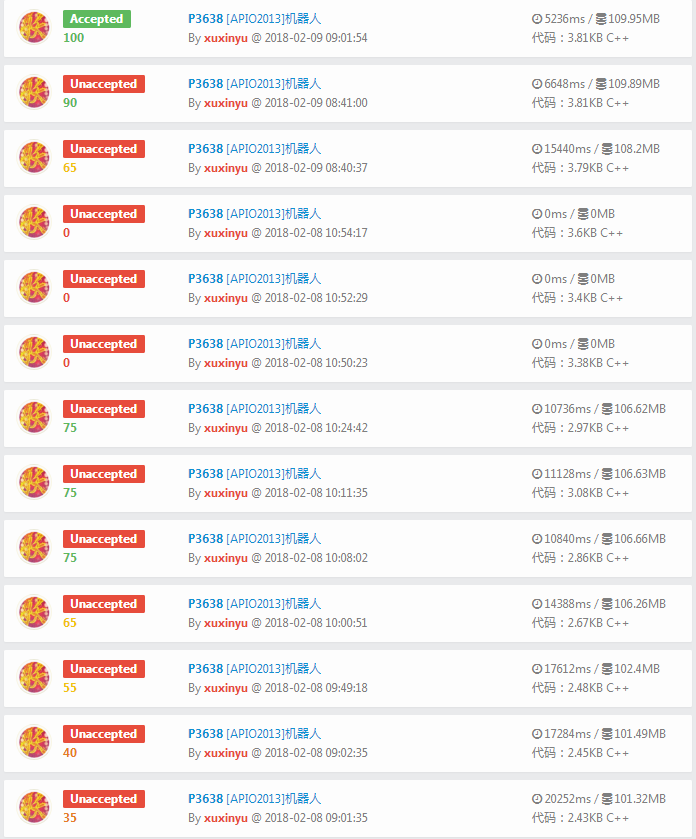
历时一天,老子终于把它A了
哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈
因为不懂spfa的优化 以及 数组越界 TAT
┭┮﹏┭┮
牢骚发完了,题解在下面 (⊙o⊙)…
n只有9,很像状压dp
dp[l][r][x][y] 表示在(x,y)位置 合成了x-y复合机器人 的最少推动次数
它的转移 存在后效性
所以上 斯坦纳树
自身的转移:dp[l][r][x][y]=min{dp[l][k][x][y]+dp[k+1][r][x][y]}
互相转移:
预处理出 在(x,y)位置 向4个方向推,最终会停留在哪个位置
可以记忆化搜索
然后用spfa
裸的spfa 得了65
加上SLF优化得了75
再加LLL优化还是75,但慢了一点儿 (可能是我不会用吧TAT)
然后改了双端队列还是75
最后参考了一位大佬的做法:
双端队列优化只是考虑 当前要入队的和在队首的 目前哪个更优
那么可以将这个扩展成单调队列,根noip2017蚯蚓很像
两个队列q1,q2
q2中存放在自身转移中入队的状态,从小到大排好序
然后由q2中转移出的状态,全部放进q1,
因为转移代价是1,q2又单调,所以可以保证q1也是单调的
每次比较q1和q2的队首,取出目前更优的状态 扩展新的状态
#include<queue> #include<cstdio> #include<cstring> using namespace std; #define N 501 typedef pair<int,int> pii; #define MP(x,y) make_pair(x,y) int T,m,n; char s[N]; int map[N][N]; int dx[4]={-1,0,1,0}; int dy[4]={0,1,0,-1}; int pos[4][N][N]; bool v[4][N][N]; int dp[10][10][N][N]; int tot,mx; int cnt[N*N*3]; pii tmp[N*N],q[N*N]; queue<pii>q1,q2; bool vis[N][N]; inline int &min(int &x,int &y) { return x<y ? x: y; } bool inmap(int x,int y) { if(x<=0 || x>n || y<=0 || y>m) return false; if(!map[x][y]) return false; return true; } int find(int x,int y,int d) { if(pos[d][x][y]) return pos[d][x][y]; if(!map[x][y]) return -2; if(v[d][x][y]) return -1; v[d][x][y]=true; int nd=d; if(map[x][y]==-1) nd=(d-1+4)%4; if(map[x][y]==-2) nd=(d+1)%4; int npos=-1; if(!inmap(x+dx[nd],y+dy[nd])) npos=-2; else npos=find(x+dx[nd],y+dy[nd],nd); v[d][x][y]=false; if(npos==-2) return pos[d][x][y]=(x-1)*m+y; else return pos[d][x][y]=npos; } void spfa(int l,int r) { for(int i=0;i<=mx;++i) cnt[i]=0; for(int i=1;i<=tot;++i) cnt[dp[l][r][tmp[i].first][tmp[i].second]]++; for(int i=1;i<=mx;++i) cnt[i]+=cnt[i-1]; for(int i=tot;i;--i) q[cnt[dp[l][r][tmp[i].first][tmp[i].second]]--]=tmp[i]; for(int i=1;i<=tot;++i) q2.push(q[i]); int x,y,nx,ny; while(!q2.empty() || !q1.empty()) { if(q1.empty()) { x=q2.front().first; y=q2.front().second; q2.pop(); } else if(q2.empty()) { x=q1.front().first; y=q1.front().second; q1.pop(); vis[x][y]=false; } else if(dp[l][r][q1.front().first][q1.front().second]>dp[l][r][q2.front().first][q2.front().second]) { x=q2.front().first; y=q2.front().second; q2.pop(); } else { x=q1.front().first; y=q1.front().second; q1.pop(); vis[x][y]=false; } for(int i=0;i<4;++i) { if(pos[i][x][y]==-1) continue; nx=(pos[i][x][y]-1)/m+1; ny=pos[i][x][y]-(nx-1)*m; if(dp[l][r][x][y]+1<dp[l][r][nx][ny]) { dp[l][r][nx][ny]=dp[l][r][x][y]+1; if(!vis[nx][ny]) q1.push(MP(nx,ny)),vis[nx][ny]=true; } } } } int main() { scanf("%d%d%d",&T,&m,&n); for(int i=1;i<=n;++i) { scanf("%s",s+1); for(int j=1;j<=m;++j) if(s[j]=='A') map[i][j]=-1; else if(s[j]=='C') map[i][j]=-2; else if(s[j]>='1' && s[j]<='9') map[i][j]=s[j]-'0'; else if(s[j]=='.') map[i][j]=10; } for(int d=0;d<4;++d) { for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) if(map[i][j]) find(i,j,d); } memset(dp,63,sizeof(dp)); int oo=dp[0][0][0][0]; for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) if(map[i][j]>=1 && map[i][j]<=9) dp[map[i][j]][map[i][j]][i][j]=0; for(int i=T;i;--i) for(int j=i;j<=T;++j) { tot=mx=0; for(int x=1;x<=n;++x) for(int y=1;y<=m;++y) { for(int k=i;k<j;++k) dp[i][j][x][y]=min(dp[i][j][x][y],dp[i][k][x][y]+dp[k+1][j][x][y]); if(dp[i][j][x][y]!=oo) tmp[++tot]=MP(x,y),mx=max(mx,dp[i][j][x][y]); } if(tot) spfa(i,j); } int ans=oo; for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) ans=min(ans,dp[1][T][i][j]); if(ans==oo) printf("-1"); else printf("%d",ans); return 0; }

