UVA 12307 Smallest Enclosing Rectangle

https://vjudge.net/problem/UVA-12307

 

求覆盖所有点的最小矩形面积、周长

 

相当于求凸包的最小面积外接矩形、最小周长外接矩形

结论：

这个矩形一定有一条边和凸包上一条边重合

证明去看https://wenku.baidu.com/view/f11d0836ee06eff9aef807d9.html

 

 

 

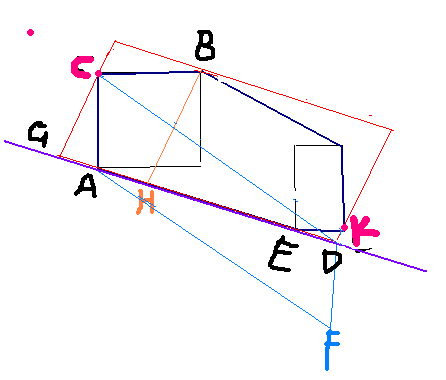
枚举一条边，用旋转卡壳求其他三边

假设现在正枚举到A点，对应紫色边，

显然，紫色边的对边一定 过A点的对踵点且与紫色边平行

那么矩形的高|BH|=AE、AB的叉积/ | AB | 

现在只剩下|GD|

把向量CD平移至向量AF

|GD|=cos(∠CDG)*|CD|=cos(∠CDG)*|AF|

AF*AD=|AF|*|AD|*cos(∠DAF)

∵∠CDG=∠DAF

∴AF*AD=|GD|*|AD|

所以|GD|=AF*AD/|AD|

 

点A是枚举的，如何求点B C K？

上面说了，点B是点A的对踵点，

那么利用叉积，同底三角形面积越大，高越大 即可求出B点

 

直观上看，K点是距点A最靠右的点

即沿向量AD向右扩展

向右就可以想到两个向量点积>0

即下一个点与这个点组成的向量，如果AD与它的点积>0，K取下一个点更优

 

C点同理，点积<0

注意C是从点B开始逆时针寻找的最靠左的点

 

#include<cmath>
#include<cstdio>
#include<algorithm>

#define N 100001

using namespace std;

const double eps=1e-9;

int dcmp(double x)
{
    if(fabs(x)<eps) return 0;
    return x<0 ? -1 : 1;
}

struct Point 
{
    double x,y;
    
    Point(double x=0,double y=0) : x(x),y(y) { }
    
    bool operator < (Point p) const
    {
        if(!dcmp(x-p.x)) return y<p.y;
        return x<p.x;
    }
    
    bool operator == (Point p) const
    {
        return !dcmp(x-p.x) && !dcmp(y-p.y);
    }
};

typedef Point Vector;

Point P[N],C[N];

Vector operator - (Vector A,Vector B) { return Vector(A.x-B.x,A.y-B.y); }

double Cross(Vector A,Vector B) 
{
    return A.x*B.y-A.y*B.x;
}

double Area2(Point A,Point B,Point D)
{
    return Cross(B-A,D-A);
}

double Dot(Vector A,Vector B)
{
    return A.x*B.x+A.y*B.y;
}

double Length(Vector A)
{
    return sqrt(Dot(A,A));
}

int ConvexHull(Point *p,int n,Point *c)
{
    sort(p,p+n);
    n=unique(p,p+n)-p;
    int m=0;
    for(int i=0;i<n;++i)
    {
        while(m>1 && Cross(c[m-1]-c[m-2],p[i]-c[m-2])<=0) 
            m--;
        c[m++]=p[i];
    }
    int k=m;
    for(int i=n-2;i>=0;--i)
    {
        while(m>k && Cross(c[m-1]-c[m-2],p[i]-c[m-2])<=0)
         m--;
        c[m++]=p[i];
    }
    m--;
    return m;
}

void RotatingCaliper(Point *c,int m)
{
    double AnsArea=1e20,AnsPeri=1e20;
    int q=1,l=0,r=0;
    double d,h,w;
    for(int p=0;p<m;++p)
    {
        while(fabs(Cross(c[p]-c[p+1],c[q+1]-c[p+1]))>fabs(Cross(c[p]-c[p+1],c[q]-c[p+1]))) q=(q+1)%m;
        while(dcmp(Dot(c[p+1]-c[p],c[r+1]-c[r]))>0) r=(r+1)%m;
        if(!l) l=q;
        while(dcmp(Dot(c[p+1]-c[p],c[l+1]-c[l]))<0) l=(l+1)%m;
        d=Length(c[p+1]-c[p]);
        h=fabs(Area2(c[p],c[p+1],c[q]))/d;
        w=Dot(c[p+1]-c[p],c[r]-c[l])/d;
        AnsArea=min(AnsArea,w*h);
        AnsPeri=min(AnsPeri,(w+h)*2);
    }
    printf("%.2lf %.2lf\n",AnsArea,AnsPeri);
}

int main()
{
    int n,m;
    while(1)
    {
        scanf("%d",&n);
        if(!n) return 0;
        for(int i=0;i<n;++i) scanf("%lf%lf",&P[i].x,&P[i].y);
        m=ConvexHull(P,n,C);
        RotatingCaliper(C,m);
    }
}