bzoj千题计划196:bzoj4826: [Hnoi2017]影魔
http://www.lydsy.com/JudgeOnline/problem.php?id=4826
吐槽一下bzoj这道题的排版是真丑。。。
我还是粘洛谷的题面吧。。。
提供p1的攻击力:i,j 位置的数是区间[i,j]的最大值和次大值
提供p2的攻击力:i,j位置的数有一个是区间[i,j]的最大值,另一个不是次大值
记录L[i]、R[i] 分别表示i左右第一个大于k[i]的位置
p1的贡献:
1、点对(L[i],R[i]) 2、点对(i,i+1)
p2的贡献:
1、点对(L[i],i+1),(L[i],i+2),……,(L[i],R[i]-1) 这些区间的最大值在L[i],次大值在i
2、点对(i-1,R[i]),(i-2,R[i]),……,(L[i+1],R[i]) 这些区间的最大值在R[i],次大值在i
然后问题就变成了
二维平面上单点修改,区间修改,矩阵查询
主席树(或许它叫可持久化线段树)可搞
第i颗线段树维护前i行的信息
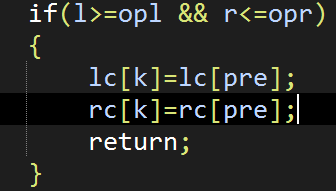
主席树实现区间修改时出现了个bug,调了一下午+一晚上~~~~(>_<)~~~~
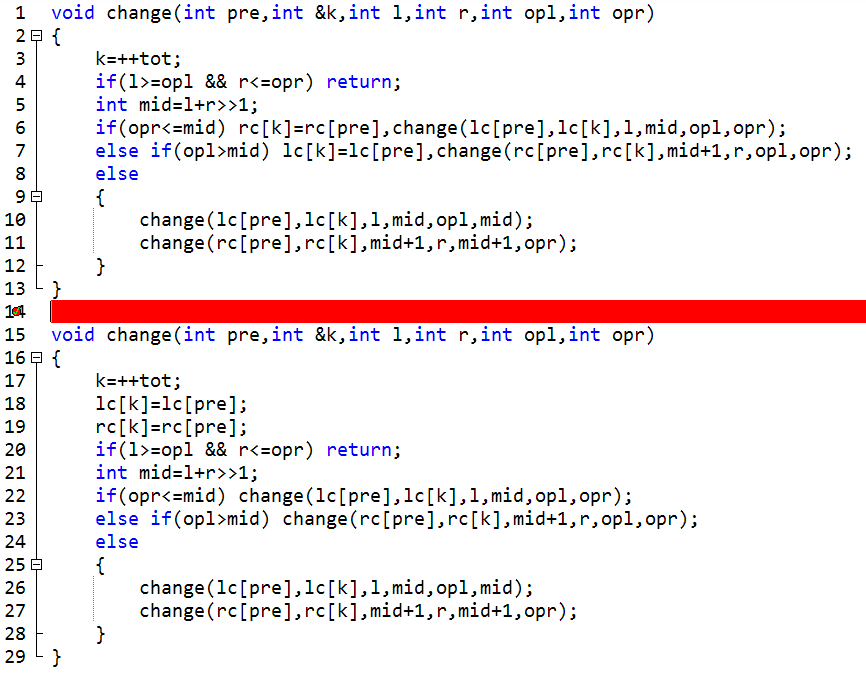
上面的写法是不对的,第4行,当区间被包含时,lc,rc 赋不上值,可能会丢失之前的部分信息
改成这样就好啦
#include<cstdio> #include<iostream> #include<algorithm> using namespace std; #define N 200001 typedef long long LL; int a[N]; int st[N][2],top; int L[N],R[N]; struct node { int x,y; }A[N]; struct node2 { int x,yl,yr; }B[N<<1]; LL num; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } int root[2][N]; struct TREE { int lc[N*30],rc[N*30]; LL sum[N*30]; int tag[N*30]; int tot; void insert(int pre,int &k,int l,int r,int opl,int opr) { k=++tot; tag[k]=tag[pre]; sum[k]=sum[pre]+opr-opl+1; lc[k]=lc[pre]; rc[k]=rc[pre]; if(l>=opl && r<=opr) { tag[k]++; return; } int mid=l+r>>1; if(opr<=mid) insert(lc[pre],lc[k],l,mid,opl,opr); else if(opl>mid) insert(rc[pre],rc[k],mid+1,r,opl,opr); else { insert(lc[pre],lc[k],l,mid,opl,mid); insert(rc[pre],rc[k],mid+1,r,mid+1,opr); } } void query(int x,int pre,int l,int r,int opl,int opr) { if(l>=opl && r<=opr) { num+=sum[x]-sum[pre]; return; } int mid=l+r>>1; if(opr<=mid) { num+=(tag[x]-tag[pre])*(opr-opl+1); query(lc[x],lc[pre],l,mid,opl,opr); } else if(opl>mid) { num+=(tag[x]-tag[pre])*(opr-opl+1); query(rc[x],rc[pre],mid+1,r,opl,opr); } else { num+=(tag[x]-tag[pre])*(mid-opl+1); query(lc[x],lc[pre],l,mid,opl,mid); num+=(tag[x]-tag[pre])*(opr-mid); query(rc[x],rc[pre],mid+1,r,mid+1,opr); } } }tr[2]; bool cmp1(node p,node q) { return p.x<q.x; } bool cmp2(node2 p,node2 q) { return p.x<q.x; } int main() { //freopen("sf1.in","r",stdin); //freopen("my.out","w",stdout); int n,m,p1,p2; read(n); read(m); read(p1); read(p2); for(int i=1;i<=n;++i) read(a[i]); st[top][0]=n+1; st[top][1]=0; for(int i=1;i<=n;++i) { while(top && a[i]>st[top][0]) top--; L[i]=st[top][1]; st[++top][0]=a[i]; st[top][1]=i; } st[top=0][0]=n+1; st[top][1]=n+1; for(int i=n;i;--i) { while(top && a[i]>st[top][0]) top--; R[i]=st[top][1]; st[++top][0]=a[i]; st[top][1]=i; } int cnt=0; for(int i=1;i<=n;++i) if(L[i] && R[i]<=n) { A[++cnt].x=L[i]; A[cnt].y=R[i]; } sort(A+1,A+cnt+1,cmp1); int now=1; for(int i=1;i<=cnt;++i) { while(now+1<A[i].x) root[0][now+1]=root[0][now],now++; tr[0].insert(root[0][now],root[0][A[i].x],1,n,A[i].y,A[i].y); now=A[i].x; } while(now!=n) root[0][now+1]=root[0][now++]; cnt=0; for(int i=1;i<=n;++i) { if(R[i]!=i+1 && L[i]) { B[++cnt].x=L[i]; B[cnt].yl=i+1; B[cnt].yr=R[i]-1; } if(L[i]!=i-1 && R[i]<=n) { B[++cnt].x=R[i]; B[cnt].yl=L[i]+1; B[cnt].yr=i-1; } } sort(B+1,B+cnt+1,cmp2); now=1; for(int i=1;i<=cnt;++i) { while(now+1<B[i].x) root[1][now+1]=root[1][now],now++; tr[1].insert(root[1][now],root[1][B[i].x],1,n,B[i].yl,B[i].yr); now=B[i].x; if(tr[1].tag[10]) { int as=4; } } while(now!=n) root[1][now+1]=root[1][now++]; int l,r; LL ans; while(m--) { read(l); read(r); num=0; tr[0].query(root[0][r],root[0][l-1],1,n,l,r); ans=num*p1; num=0; tr[1].query(root[1][r],root[1][l-1],1,n,l,r); ans+=num*p2; ans+=(r-l)*p1; cout<<ans<<'\n'; } }
题目背景
影魔,奈文摩尔,据说有着一个诗人的灵魂。 事实上,他吞噬的诗人灵魂早已成千上万。
千百年来,他收集了各式各样的灵魂,包括诗人、 牧师、 帝王、 乞丐、 奴隶、 罪人,当然,还有英雄。
题目描述
每一个灵魂,都有着自己的战斗力,而影魔,靠这些战斗力提升自己的攻击。
奈文摩尔有 n 个灵魂,他们在影魔宽广的体内可以排成一排,从左至右标号 1 到 n。第 i个灵魂的战斗力为 k[i],灵魂们以点对的形式为影魔提供攻击力,对于灵魂对 i, j(i<j)来说,若不存在 ks大于 k[i]或者 k[j],则会为影魔提供 p1 的攻击力(可理解为: 当 j=i+1 时,因为不存在满足 i<s<j 的 s,从而 k[s]不存在,这时提供 p1 的攻击力;当 j>i+1 时,若max{k[s]|i<s<j}<=min{k[i],k[j]} , 则 提 供 p1 的 攻 击 力 ); 另 一 种 情 况 , 令 c 为k[i+1],k[i+2],k[i+3]……k[j-1]的最大值,若 c 满足: k[i]<c<k[j],或者 k[j]<c<k[i],则会为影魔提供 p2 的攻击力,当这样的 c 不存在时,自然不会提供这 p2 的攻击力;其他情况的点对,均不会为影魔提供攻击力。
影魔的挚友噬魂鬼在一天造访影魔体内时被这些灵魂吸引住了,他想知道,对于任意一段区间[a,b], 1<=a<b<=n,位于这些区间中的灵魂对会为影魔提供多少攻击力,即考虑 所有满足a<=i<j<=b 的灵魂对 i,j 提供的攻击力之和。
顺带一提,灵魂的战斗力组成一个 1 到 n 的排列: k[1],k[2],…,k[n]。
输入输出格式
输入格式:
输入文件名为 sf.in。
第一行 n,m,p1,p2
第二行 n 个数: k[1],k[2],…,k[n]
接下来 m 行, 每行两个数 a,b, 表示询问区间[a,b]中的灵魂对会为影魔提供多少攻击力。
输出格式:
输出文件名为 sf.out
共输出 m 行,每行一个答案,依次对应 m 个询问。
输入输出样例
说明
30%: 1<= n,m <= 500。
另 30%: p1=2*p2。
100%:1 <= n,m <= 200000; 1 <= p1,p2 <= 1000。

