2017 清北济南考前刷题Day 4 afternoon
期望得分:30+50+30=110
实际得分:40+0+0=40
并查集合并再次写炸。。。

模拟更相减损术的过程
更相减损术,差一定比被减数小,当被减数=减数时,停止
对于同一个减数来说,会被减 第1次减这个减数的被减数/这个减数 次
然后这个减数成为被减数,减数变为 原被减数-k*原减数,即原被减数%原减数
就变成了辗转相除

#include<cstdio> #include<iostream> using namespace std; typedef long long LL; LL ans; void gcd(LL a,LL b) { if(!b) { ans++; return; } ans+=a/b; gcd(b,a%b); } int main() { freopen("seq.in","r",stdin); freopen("seq.out","w",stdout); LL a,b; cin>>a>>b; gcd(a,b); cout<<ans; }

首先可以确定最终的销售度取决于最大生成树上的边
从大到小枚举 每一条边,直至加入了n-1 条边
对于每一条可以加入的边,不是直接像最大生成树那样直接连边
而是新建一个节点,这条边的两个点作为新节点的左右子节点
新节点的权值为这条边的重量限制
这样建出一颗二叉树,二叉树的叶子节点就是原来的城市
且二叉树的非叶子节点的权值 自底向上 递减
设二叉树非叶子节点k的左右子节点分别为l,r,对应的子树大小为siz,k的权值为w
那么它可以表示 在l 重量为w 的 车 比 重量 为w+1 的车 能多到siz[k]-siz[l]个城市
在r 重量为w的车比重量为w+1的长 能多到siz[k]-siz[r] 个城市
如果所有边的重量限制不一样,
那么每个城市的销售度的和=城市到根节点路径上相邻节点子树大小的差 的 平方和,前缀和统计即可
如果有的边的重量限制一样,
在父节点能到的城市,在这儿也能到,这对相邻节点就没有贡献,同时让这个点的siz=父节点的siz

#include<cstdio> #include<iostream> #include<algorithm> using namespace std; #define N 100001 #define M 500001 typedef long long LL; struct node { int u,v,w; }e[M]; int tr[N<<1][2]; int fa[N<<1],siz[N<<1]; int val[N<<1]; LL ans[N]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } bool cmp(node p,node q) { return p.w>q.w; } void dfs(int x,int fa,LL w) { LL delta=0; if(fa) { if(val[fa]==val[x]) siz[x]=siz[fa]; else delta=(LL)(siz[fa]-siz[x])*(siz[fa]-siz[x]); } if(tr[x][0]) { dfs(tr[x][0],x,w+delta); dfs(tr[x][1],x,w+delta); } else ans[x]=w+delta; } int find(int i) { return fa[i]==i ? i : fa[i]=find(fa[i]); } int main() { freopen("car6.in","r",stdin); //freopen("car.out","w",stdout); int n,m; read(n); read(m); for(int i=1;i<=n;i++) fa[i]=i,siz[i]=1; for(int i=1;i<=m;i++) read(e[i].u),read(e[i].v),read(e[i].w); sort(e+1,e+m+1,cmp); int tot=0; int u,v; int sum=n; for(int i=1;i<=m && tot!=n-1;i++) { u=find(e[i].u); v=find(e[i].v); if(u==v) continue; tot++; tr[++sum][0]=u; tr[sum][1]=v; fa[u]=fa[v]=fa[sum]=sum; val[sum]=e[i].w; siz[sum]=siz[u]+siz[v]; } dfs(sum,0,0); for(int i=1;i<=n;i++) cout<<ans[i]<<' '; }
50分暴力
从大到小加边,每加一条边暴力枚举统计 两个联通块的影响

#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 2001 #define M 20001 int n,m; struct node { int u,v,w; }e[M]; int front[N],nxt[M<<1],to[M<<1],tot; int fa[N],siz[N]; bool vis[N]; int use[N],q[N]; int ans[N][N]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } bool cmp(node p,node q) { return p.w>q.w; } void init() { read(n); read(m); for(int i=1;i<=m;i++) read(e[i].u),read(e[i].v),read(e[i].w); sort(e+1,e+m+1,cmp); for(int i=1;i<=n;i++) fa[i]=i,siz[i]=1; } int find(int i) { return fa[i]==i ? i : fa[i]=find(fa[i]); } void bfs(int s,int w,int sum) { int head=0,tail=1,cnt=0; q[0]=s; ans[s][w]+=sum; use[++cnt]=s; vis[s]=true; while(head<tail) { for(int i=front[q[head++]];i;i=nxt[i]) if(!vis[to[i]]) { vis[to[i]]=true; ans[to[i]][w]+=sum; q[tail++]=to[i]; use[++cnt]=to[i]; } } for(int i=1;i<=cnt;i++) vis[use[i]]=false; } void add(int u,int v) { to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; } void MST() { int u,v; for(int i=1;i<=m && tot!=n-1;i++) { u=e[i].u; v=e[i].v; if(find(u)==find(v)) continue; tot++; bfs(u,e[i].w,siz[fa[v]]); bfs(v,e[i].w,siz[fa[u]]); siz[fa[v]]+=siz[fa[u]]; fa[fa[u]]=fa[v]; add(u,v); } int out; for(int i=1;i<=n;i++) { out=0; for(int j=1;j<N;j++) out+=ans[i][j]*ans[i][j]; cout<<out<<' '; } } int main() { freopen("car.in","r",stdin); freopen("car.out","w",stdout); init(); MST(); }

模型:
求在有两种限制的情况下的最小值
定义f(x)表示完全满足其中一个限制,另一个限制为x时的最小值,
选取一个c,c满足 当cx-f(x) 最大时,x满足另一个限制
设cx-f(x)=s ,则 满足两个限制下的最小值=cx-s
具体到本题来说
两个限制:选k个数,选的数的距离>=m
设f(x)表示 选的数的距离>=m 时,选出x个数的最小值
二分一个c,c满足 当cx-f(x)最大时,x=k
设cx-f(x)=s,则选出k个数,每个数的距离>=m的最小值=cx-s
如何检验二分出的c?
令dp[i] 表示 到第i个数,选出的每个数的距离>=m 的最大值
f[i] 表示 在满足dp[i]时,最少取多少个数
不选,由i-1转移
选,由i-m 转移
若f[n]<=k , c下调,否则,c上调
c的意义:
c 是 f(x) 的斜率

当 cx-f(x)取得最大值时,若x=k,则
直线 cx 与 点(k+1,f(k+1))和点(k,f(k))构成的直线平行
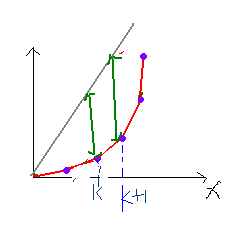
当取值最大的x>=k 时,要下调c

取值最大位置<k 时,上调c

#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 1000001 int a[N]; int n,m; long long dp[N]; int f[N]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } long long getsum(long long t) { memset(dp,0,sizeof(dp)); for(int i=1;i<=n;i++) if(i<=m) dp[i]=max(dp[i-1],t-a[i]); else dp[i]=max(dp[i-1],dp[i-m]+t-a[i]); return dp[n]; } int check(long long mid) { memset(dp,0,sizeof(dp)); memset(f,0,sizeof(f)); for(int i=1;i<=n;i++) if(i<=m) { if(mid-a[i]>dp[i-1]) dp[i]=mid-a[i],f[i]=1; else dp[i]=dp[i-1],f[i]=f[i-1]; } else { if(dp[i-m]+mid-a[i]>dp[i-1]) dp[i]=dp[i-m]+mid-a[i],f[i]=f[i-m]+1; else if(dp[i-m]+mid-a[i]==dp[i-1]) dp[i]=dp[i-1],f[i]=min(f[i-1],f[i-m]+1); else dp[i]=dp[i-1],f[i]=f[i-1]; } // cout<<mid<<' '<<f[n]<<'\n'; return f[n]; } int main() { freopen("number.in","r",stdin); freopen("number.out","w",stdout); int k; read(n); read(m); read(k); for(int i=1;i<=n;i++) read(a[i]); long long l=0,r=1LL*10000000*n,mid,c; while(l<=r) { mid=l+r>>1; if(check(mid)>=k) c=mid,r=mid-1; else l=mid+1; } cout<<c*k-getsum(c); }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号