2017 清北济南考前刷题Day 2 afternoon
期望得分:100+60+70=230
实际得分:0+60+0=60
T1

可以证明如果一对括号原本就匹配,那么这对括号在最优解中一定不会被分开
所以用栈记录下没有匹配的括号
最后栈中一定是 一堆右括号然后一堆左括号
ans=栈中右括号/2 上取整 + 栈中左括号 /2 上取整

#include<cstdio> #include<cstring> using namespace std; #define N 100001 int top; char st[N]; char s[N]; int main() { freopen("shower.in","r",stdin); freopen("shower.out","w",stdout); scanf("%s",s+1); int len=strlen(s+1); for(int i=1;i<=len;i++) if(s[i]=='(') st[++top]='('; else if(top && st[top]=='(') top--; else st[++top]=')'; int ans=0; int i; for(i=1;i<=top;i++) if(st[i]!=')') break; i--; printf("%d",(i+1)/2+(top-i+1)/2); }
考试的时候 碰到右括号,没有判断此时栈顶是否是左括号
括号匹配只需要判断 栈中是否有东西,因为一定是 左括号
这里因为有不合法的情况,所以需要判断
T2

前缀和二分

#include<cstdio> #include<iostream> #define N 1000004 using namespace std; bool vis[N]; int p[N],cnt; long long sum[N]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } void pre() { for(int i=2;i<N;i++) { if(!vis[i]) { p[++cnt]=i; sum[cnt]=sum[cnt-1]+p[cnt]; } for(int j=1;j<=cnt;j++) { if(i*p[j]>=N) break; vis[i*p[j]]=true; if(i%p[j]==0) break; } } } int main() { freopen("diary.in","r",stdin); freopen("diary.out","w",stdout); pre(); int T,n,k; read(T); int l,r,mid,tmp; while(T--) { read(n); read(k); l=k;r=lower_bound(p+1,p+cnt+1,n)-p; tmp=-1; while(l<=r) { mid=l+r>>1; if(sum[mid]-sum[mid-k]<=n) tmp=mid,l=mid+1; else r=mid-1; } printf("%d\n",tmp==-1 ? -1 : sum[tmp]-sum[tmp-k]); } }
60 暴力

#include<cstdio> #include<iostream> #include<algorithm> using namespace std; int T; #define N 1000004 typedef long long LL; int p[N],cnt; bool vis[N]; LL sum[N]; struct node { int n,k,id; }e[2001]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } void pre() { for(int i=2;i<N;i++) { if(!vis[i]) p[++cnt]=i; for(int j=1;j<=cnt;j++) { if(i*p[j]>=N) break; vis[i*p[j]]=true; if(i%p[j]==0) break; } } for(int i=1;i<=cnt;i++) sum[i]=sum[i-1]+p[i]; } namespace solve1 { void work() { int n,k,m; bool ok; for(int i=1;i<=T;i++) { n=e[i].n; k=e[i].k; m=lower_bound(p+1,p+cnt,n)-p; ok=false; for(int i=m;i>=k && !ok ;i--) if(sum[i]-sum[i-k]<=n) { printf("%d\n",sum[i]-sum[i-k]); ok=true; } if(!ok) puts("-1"); } } } namespace solve2 { int ans[2001]; bool cmp(node p,node q) { return p.k<q.k; } void work() { sort(e+1,e+T+1,cmp); int r=lower_bound(p+1,p+cnt+1,e[1].n)-p; int l=r; int now=1; while(now<=T) { l=min(l,r-e[now].k+1); if(l<=0) break; while(l>1 && sum[r]-sum[l-1]>e[now].n) r--,l--; if(sum[r]-sum[l-1]>e[now].n) break; ans[e[now].id]=sum[r]-sum[l-1]; now++; } for(;now<=T;now++) ans[e[now].id]=-1; for(int i=1;i<=T;i++) printf("%d\n",ans[i]); } } void init() { read(T); bool flag1=true,flag2=true; for(int i=1;i<=T;i++) { read(e[i].n); read(e[i].k); if(e[i].n>100) flag1=false; if(e[i].n!=e[1].n) flag2=false; e[i].id=i; } if(flag1 || T==1) solve1::work(); else if(flag2) solve2::work(); } int main() { freopen("diary.in","r",stdin); freopen("diary.out","w",stdout); pre(); init(); }
T3

这算个DP套DP吗
设g[i][j] 表示 在第i棵树中,所有的点到j的权值和
F(t)=F(a)+F(b)+ size[a]*size[b]*l + g[a][c]*size[b] + g[b][d]*size[a]
size在合并的过程中 维护即可
求 g[i][j] :
设dis[i][j][k] 在第i棵树中,j到k的距离
设现在要求g[t][k],有一条长为L的边连接c和d
g[t][k]=g[A][k]+g[B][d]+(L+dis[A][k][c])*size[B]
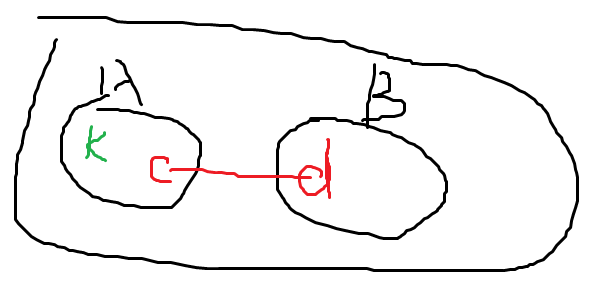
求dis[i][j][k]:
如果本就是在一棵树里,直接= dis[A][j][k]
否则
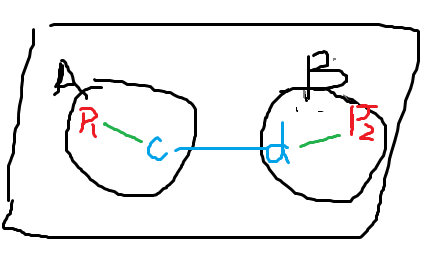
假设有一条长为L的边连接了树A中第点c和树B中的点d,构成了第t棵树
现在要求dis[t][p1][p2]
=dis[A][c][p1]+dis[B][d][p2]+L
g数组和dis数组不可能都存下来,每一次合并只涉及两个点,记忆化搜索即可
注意:如果某点是在合并的第二棵树里,编号还要减去第一棵树的大小

#include<map> #include<cstdio> #include<iostream> #include<algorithm> using namespace std; typedef long long LL; const int mod=1e9+7; struct node { int p; LL p1,p2; node() {} node(int i,LL j,LL k) { p=i; p1=min(j,k); p2=max(j,k); } bool operator < (node a) const { if(p!=a.p) return p<a.p; if(p1!=a.p1) return p1<a.p1; return p2<a.p2; } }; map<pair<int,LL>,int>g; map<node,int>dis; int id1[61],id2[61],len[61]; LL num1[61],num2[61]; LL siz[61]; int f[61]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } void read(LL &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-'0'; c=getchar(); } } int getDIS(int i,LL j,LL k) { if(!i) return 0; if(j==k) return 0; node x=node(i,j,k); if(dis.count(x)) return dis[x]; if(j<siz[id1[i]]) { if(k<siz[id1[i]]) return dis[x]=getDIS(id1[i],j,k); return dis[x]=(1LL*getDIS(id1[i],num1[i],j)+len[i]+getDIS(id2[i],num2[i],k-siz[id1[i]]))%mod; } else { if(k<siz[id1[i]]) return dis[x]=(1LL*getDIS(id1[i],num1[i],k)+len[i]+getDIS(id2[i],num2[i],j-siz[id1[i]]))%mod; return dis[x]=getDIS(id2[i],j-siz[id1[i]],k-siz[id1[i]]); } } int getG(int i,LL j) { if(!i) return 0; pair<int,LL>pr = make_pair(i,j); if(g.count(pr)) return g[pr]; if(j<siz[id1[i]]) return g[pr]=((1LL*getDIS(id1[i],num1[i],j)+len[i])*(siz[id2[i]]%mod)%mod+getG(id2[i],num2[i])+getG(id1[i],j))%mod; return g[pr]=((1LL*getDIS(id2[i],num2[i],j-siz[id1[i]])+len[i])*(siz[id1[i]]%mod)%mod+getG(id1[i],num1[i])+getG(id2[i],j-siz[id1[i]]))%mod; } int main() { freopen("cloth.in","r",stdin); freopen("cloth.out","w",stdout); int m; read(m); siz[0]=1; for(int i=1;i<=m;i++) { read(id1[i]); read(id2[i]); read(num1[i]); read(num2[i]); read(len[i]); f[i]=(f[id1[i]]+f[id2[i]]+(siz[id1[i]]%mod)*(siz[id2[i]]%mod)%mod*len[i]%mod+getG(id1[i],num1[i])*(siz[id2[i]]%mod)%mod+getG(id2[i],num2[i])*(siz[id1[i]]%mod)%mod)%mod; siz[i]=siz[id1[i]]+siz[id2[i]]; cout<<f[i]<<'\n'; } }



